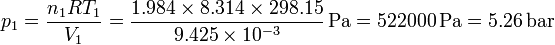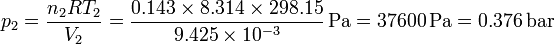Variación de entropía de dos cámaras de gas

De Laplace

Revisión a fecha de 21:59 18 mar 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

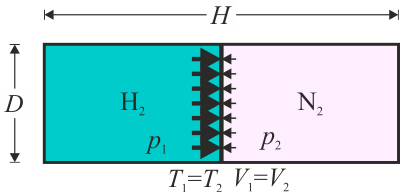
Se tiene un cilindro de 20 cm de diámetro y 60 cm de longitud paredes diatermas en el interior del cual hay dos cámaras de gas. En una hay 4 g de H₂ y en la otra 4 g de N₂. La temperatura de los dos gases es de 25°C, que también es la temperatura exterior. Separando los dos gases hay un émbolo inicialmente fijado en el centro.

Se libera el pistón y se espera hasta que se vuelva a quedar en equilibrio el sistema. Halle el incremento de entropía de cada gas, del sistema, del entorno y del universo.

Si en vez de liberar el pistón le hacemos un agujero, ¿cuáles son las variaciones de entropía correspondientes?

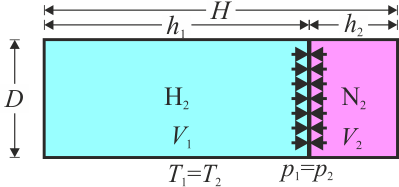
2 Desplazamiento del pistón

Este problema es una continuación del problema “Tubo con dos cámaras de gas”. Tal como se ve en la solución de dicho problema, inicialmente tenemos diferentes presiones en las cámaras, porque aunque estén a la misma temperatura y ocupen el mismo volumen,

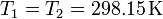
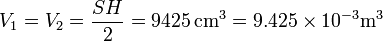
$T_1 = T_2 = 298.15\,\mathrm{K}$ $V_1 = V_2 = \frac{SH}{2} = 9425\,\mathrm{cm}^3 = 9.425\times 10^{-3}\mathrm{m}^3$

el número de moles de cada gas es diferente. Para el hidrógeno

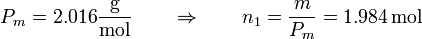
$P_m = 2.016\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_1 = \frac{m}{P_m} = 1.984\,\mathrm{mol}$

y para el nitrógeno

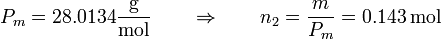
$P_m = 28.0134\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_2 = \frac{m}{P_m} = 0.143\,\mathrm{mol}$

siendo las presiones iniciales

$p_1 = \frac{n_1 R T_1}{V_1}= \frac{1.984\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 522000\,\mathrm{Pa} = 5.26\,\mathrm{bar}$ $p_2 = \frac{n_2 R T_2}{V_2}= \frac{0.143\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 37600\,\mathrm{Pa} = 0.376\,\mathrm{bar}$