Dinámica de los sistemas de partículas (GIE)

De Laplace

Revisión a fecha de 16:57 28 nov 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Definición de sistema de partículas
2 Propiedades de un sistema de partículas
3 Leyes de conservación
4 Aplicaciones
- 4.1 Sistema de dos partículas
5 Colisiones
6 Definición
7 Choques unidimensionales
8 Conservación de la cantidad de movimiento
9 Conservación de la energía
- 9.1 Coeficiente de restitución
10 Colisión perfectamente elástica
- 10.1 Choque de dos masas iguales
- 10.2 Caso de un blanco en reposo
  - 10.2.1 Blanco masivo
  - 10.2.2 Blanco ligero
11 Colisión completamente inelástica
12 Colisiones en tres dimensiones

1 Definición de sistema de partículas

En mecánica consideramos un sistema de partículas como un conjunto de $N$ puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas.

Cada una de las partículas del sistema posee una masa propia, $m i$ , siendo 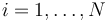$i=1,\ldots,N$ un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula $i$ está caracterizada por una posición 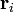$\mathbf{r}_i$ y una velocidad 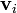$\mathbf{v}_i$ . Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica

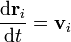
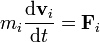
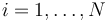
$\frac{\mathrm{d}\mathbf{r}_i}{\mathrm{d}t}=\mathbf{v}_i$ $m_i \frac{\mathrm{d}\mathbf{v}_i}{\mathrm{d}t} = \mathbf{F}_i$ $i=1,\ldots,N$

siendo 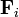$\mathbf{F}_i$ la resultante de las fuerzas que actúan sobre la partícula $i$ . Esta resultante se compone de las fuerzas que cada una de las demás partículas del sistema ejerce sobre $i$ , más la resultante de las fuerzas externas aplicadas sobre ella

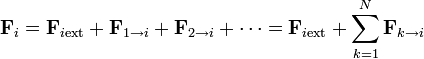
$\mathbf{F}_i = \mathbf{F}_{i\mathrm{ext}}+ \mathbf{F}_{1\to i}+\mathbf{F}_{2\to i} + \cdots = \mathbf{F}_{i\mathrm{ext}}+\sum_{k=1}^N \mathbf{F}_{k\to i}$

Este sumatorio representa la suma sobre las partículas restantes, esto es $k$ va de $1$ hasta $N$ , excluyendo el caso $k = i$ , ya que admitimos que una partícula no produce fuerza sobre sí misma (equivalentemente, 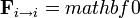$\mathbf{F}_{i\to i}=ºmathbf{0}$ ).

Suponemos que las interacciones entre las partículas obdecen la 3ª ley de Newton

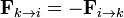
$\mathbf{F}_{k\to i} = -\mathbf{F}_{i\to k}$

o, lo que es lo mismo

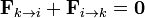
$\mathbf{F}_{k\to i} +\mathbf{F}_{i\to k} = \mathbf{0}$

En la mayoría de los casos se cumplirá además que la fuerza que la partícula $k$ ejerce sobre la $i$ (y por tanto la que la $i$ ejerce sobre la $k$ ) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector 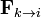$\mathbf{F}_{k\to i}$ es paralelo a la posición relativa 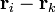$\mathbf{r}_i-\mathbf{r}_k$ , esto es, si

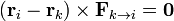
$(\mathbf{r}_{i}-\mathbf{r}_k)\times\mathbf{F}_{k\to i} = \mathbf{0}$

Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición

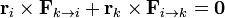
$\mathbf{r}_i\times\mathbf{F}_{k\to i} + \mathbf{r}_k \times \mathbf{F}_{i\to k} = \mathbf{0}$

2 Propiedades de un sistema de partículas

Un sistema de partículas puede contener 2 o 3 partículas, pero también muchos miles de millones de ellas (por ejemplo 1 cm³ de agua contiene 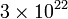$3\times 10^{22}$ moléculas, cada una de las cuales contiene 26 partículas, entre protones, neutrones y electrones). Por ello, en la mayoría de los casos no es posible estudiar un sistema de partículas a partir de la evolución de cada uno de las partículas que lo forman (entre otras cosas, porque desconocemos la posición y la velocidad exacta de cada una).

En su lugar, nos restringimos a considerarlas colectivamente, definiendo propiedades del conjunto, que cumplen sus propias leyes de evolución. Esta reducción es particularmente útil en el caso del sólido rígido, para el cual las magnitudes que vamos a definir a continuación son suficientes para determinar la evolución del sistema completo.

2.1 Masa total

La masa total del sistema es la suma de las masas de los partículas que lo componen

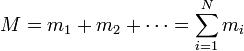
$M = m_1 + m_2 + \cdots = \sum_{i=1}^N m_i$

2.1.1 Densidad de masa

Cuando tenemos un sistema de muchos millones de partículas (como en un sólido, o un fluido), no es práctico hacer el sumatorio de las masas individuales. En su lugar se divide el sistema en elementos de volumen, $Δτ$ , que son regiones del espacio lo suficientemente pequeñas para tratarlas como diferenciales, pero lo suficientemente grandes como para que contengan miles de partículas. El sistema se considera entonces como continuo, esto es, en lugar de describirse como formado por partículas separadas, se considera constituido por elementos de volumen adyacentes.

Se define entonces la densidad de masa, $ρ$ de un elemento de volumen, como la masa de las partículas que lo forman, dividida por el volumen del elemento

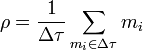
$\rho = \frac{1}{\Delta\tau} \sum_{m_i\in\Delta\tau} m_i$

Dicho de otra forma, la masa de un elemento de volumen es el producto de la densidad de masa por el volumen del elemento

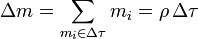
$\Delta m = \sum_{m_i\in\Delta\tau} m_i = \rho\,\Delta\tau$

La masa total del sistema será la suma de la masa de todos sus elementos

$M = \sum_{\forall\ \Delta m} \Delta m = \sum_{\forall\ \Delta\tau} \rho\,\mathrm{\Delta\tau}$

Una suma de muchas cantidades muy pequeñas no es otra cosa que una integral

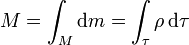
$M = \int_M \mathrm{d}m = \int_\tau \rho\,\mathrm{d}\tau$

Aquí la densidad es una función de la posición porque en un sistema no homogéneo (por ejemplo, el cuerpo humano) la densidad varía de un punto a otro.

2.2 Centro de masas

El centro de masas (CM) de un sistema de partículas es una media ponderada, según la masa individual, de las posiciones de todas las partículas que lo componen

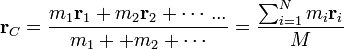
$\mathbf{r}_C = \frac{m_1\mathbf{r}_1+m_2\mathbf{r}_2+\cdots...}{m_1++m_2+\cdots} = \frac{\sum_{i=1}^N m_i\mathbf{r}_i}{M}$

Equivalentemente se cumple

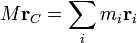
$M\mathbf{r}_C = \sum_i m_i\mathbf{r}_i$

En el caso de un sistema continuo, habrá que sumar para todos los elementos que lo componen

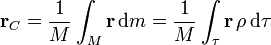
$\mathbf{r}_C = \frac{1}{M}\int_M \mathbf{r}\,\mathrm{d}m = \frac{1}{M}\int_\tau \mathbf{r}\,\rho\,\mathrm{d}\tau$

2.2.1 Velocidad del centro de masas

El centro de masas no es un punto fijo, sino que puede desplazarse cuando lo hacen las partículas del sistema. Obtenemos su velocidad derivando la definición respecto al tiempo

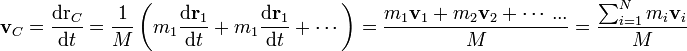
$\mathbf{v}_C = \frac{\mathrm{d}\mathrm{r}_C}{\mathrm{d}t} = \frac{1}{M}\left(m_1\frac{\mathrm{d}\mathbf{r}_1}{\mathrm{d}t}+m_1\frac{\mathrm{d}\mathbf{r}_1}{\mathrm{d}t}+\cdots\right) = \frac{m_1\mathbf{v}_1+m_2\mathbf{v}_2+\cdots...}{M} = \frac{\sum_{i=1}^N m_i\mathbf{v}_i}{M}$

2.2.2 Posición relativa al centro de masas

Una vez definida la posición del centro de masas, interesa indicar dónde están situadas las partículas respecto al CM. Esto se consigue definiendo la posición relativa

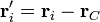
$\mathbf{r}'_i = \mathbf{r}_i-\mathbf{r}_C$

De manera análoga se define la velocidad relativa al CM

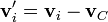
$\mathbf{v}'_i = \mathbf{v}_i-\mathbf{v}_C$

2.3 Cantidad de movimiento

La cantidad de movimiento (o momento lineal) del sistema es la suma de las cantidades de movimiento de cada una de las partículas

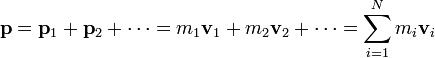
$\mathbf{p} = \mathbf{p}_1+\mathbf{p}_2+\cdots = m_1\mathbf{v}_1+m_2\mathbf{v}_2 + \cdots = \sum_{i=1}^N m_i\mathbf{v}_i$

La cantidad de movimiento se relaciona directamente con el centro de masas del sistema. Derivando respecto al tiempo la relación

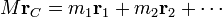
$M\mathbf{r}_C = m_1 \mathbf{r}_1 + m_2\mathbf{r}_2+\cdots$

obtenemos

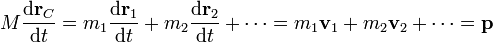
$M \frac{\mathrm{d}\mathbf{r}_C}{\mathrm{d}t} = m_1 \frac{\mathrm{d}\mathbf{r}_1}{\mathrm{d}t} + m_2\frac{\mathrm{d}\mathbf{r}_2}{\mathrm{d}t} + \cdots = m_1\mathbf{v}_1+m_2\mathbf{v}_2+\cdots = \mathbf{p}$

esto es

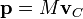
$\mathbf{p} = M \mathbf{v}_C$

En palabras: la cantidad de movimiento del sistema equivale a la que tendría una sola partícula material que concentrara toda la masa del sistema y que se moviera como el centro de masas de éste.

De la relación entre cantidad de movimiento y centro de masas se llega a que la cantidad de movimiento del sistema respecto al centro de masas es siempre nula

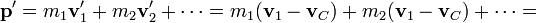
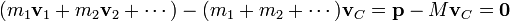
$\mathbf{p}' = m_1 \mathbf{v}'_1 + m_2\mathbf{v}'_2 + \cdots = m_1 (\mathbf{v}_1-\mathbf{v}_C) + m_2(\mathbf{v}_1-\mathbf{v}_C) + \cdots =$ $( m_1\mathbf{v}_1+m_2\mathbf{v}_2 + \cdots) - (m_1+m_2+\cdots)\mathbf{v}_C = \mathbf{p}- M \mathbf{v}_C=\mathbf{0}$

Esto permite redefinir el centro de masas como aquel punto (variable) desde el cual la cantidad de movimiento del sistema es nula en todo momento. Cuando un sistema de partículas se estudia empleando este punto como origen del sistema de referencia se dice que se está estudiando desde el sistema centro de masas.

2.4 Momento angular (o cinético)

De manera análoga a la cantidad de movimiento, se define el momento cinético (o angular) de un sistema de partículas como la suma vectorial de los momentos cinéticos individuales

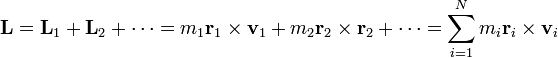
$\mathbf{L}=\mathbf{L}_1+\mathbf{L}_2 +\cdots = m_1\mathbf{r}_1\times\mathbf{v}_1+m_2\mathbf{r}_2\times\mathbf{r}_2+\cdots = \sum_{i=1}^N m_i\mathbf{r}_i\times\mathbf{v}_i$

2.4.1 Descomposición del momento angular

Las ecuaciones de la dinámica de sistemas se simplificarían notablemente si el momento angular, como el lineal, equivaliera al de una partícula puntual que concentrara toda la masa. No es así.

Para relacionar el momento angular con el centro de masa, descomponemos cada posición y cada velocidad en suma de la del centrode masa más la posición o velocidad relativas

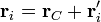
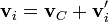
$\mathbf{r}_i = \mathbf{r}_C+\mathbf{r}'_i\,$ $\mathbf{v}_i = \mathbf{v}_C+\mathbf{v}'_i\,$

Con esta descomposición, el momento angular de cada partícula se separa en cuatro términos

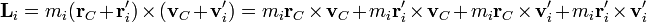
$\mathbf{L}_i = m_i(\mathbf{r}_C+\mathbf{r}'_i)\times( \mathbf{v}_C+\mathbf{v}'_i)= m_i\mathbf{r}_C\times\mathbf{v}_C+m_i\mathbf{r}'_i\times \mathbf{v}_C+m_i\mathbf{r}_C\times\mathbf{v}'_i+m_i\mathbf{r}'_i\times\mathbf{v}'_i$

Al sumar los momentos cinéticos individuales para obtener el momento angular total nos quedan cuatro sumas, en cada una de las cuales podemos sacar factor común la posición o la velocidad del CM, que es una cantidad que no depende del índice $i$

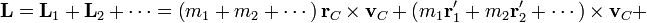
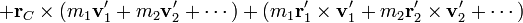
$\mathbf{L}= \mathbf{L}_1+\mathbf{L}_2 +\cdots = \left(m_1+m_2+\cdots\right)\mathbf{r}_C\times\mathbf{v}_C+\left(m_1\mathbf{r}'_1+m_2\mathbf{r}'_2+\cdots\right)\times\mathbf{v}_C +$ $+\mathbf{r}_C\times\left(m_1\mathbf {v}'_1+m_2\mathbf{v}'_2+\cdots\right)+\left(m_1\mathbf{r}'_1\times\mathbf{v}'_1+m_2\mathbf{r}'_2\times\mathbf{v}'_2+\cdots\right)$

Ahora bien, de la definición de centro de masas se deduce que

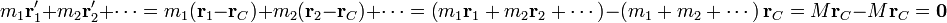
$m_1\mathbf{r}'_1+m_2\mathbf{r}'_2 +\cdots = m_1(\mathbf{r}_1-\mathbf{r}_C)+m_2(\mathbf{r}_2-\mathbf{r}_C)+\cdots = \left(m_1\mathbf{r}_1+m_2\mathbf{r}_2+\cdots\right)-\left(m_1+m_2+\cdots\right)\mathbf{r}_C = M\mathbf{r}_C-M\mathbf{r}_C = \mathbf{0}$

y, del mismo modo,

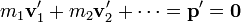
$m_1\mathbf{v}'_1 + m_2\mathbf{v}'_2 +\cdots = \mathbf{p}' = \mathbf{0}$

Por tanto, el segundo y el tercer término en la expresión del momento cinético total se anulan y la expresión se reduce a

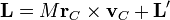
$\mathbf{L}= M\mathbf{r}_C\times\mathbf{v}_C+\mathbf{L}'$

donde

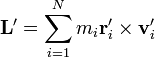
$\mathbf{L}'= \sum_{i=1}^N m_i\mathbf{r}'_i\times\mathbf{v}'_i$

es el momento angular relativo al centro de masas.

Según esto, el momento angular o cinético de un sistema de partículas se compone de dos contribuciones: el momento angular que tendría una partícula que contuviera toda la masa y se moviera como el centro de masas del sistema, más el momento angular que tienen las partículas por moverse alrededor del centro de masas.

Un ejemplo físico sencillo de esta descomposición lo tenemos en el momento angular de la Tierra en cuanto planeta del Sistema Solar. Su momento angular se compone de una parte debida al movimiento de traslación alrededor del Sol (lo que se conoce como momento angular orbital), que sería el primer término, más otra parte debida al movimiento de rotación alrededor de su eje (el llamado momento angular intrínseco), que sería 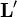$\mathbf{L}'$ .

2.5 Energía cinética

La energía cinética del sistema es la suma escalar de las energías cinéticas individuales

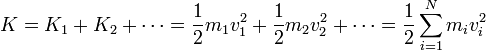
$K = K_1+K_2+\cdots = \frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2 + \cdots = \frac{1}{2}\sum_{i=1}^Nm_iv_i^2$

2.5.1 Descomposición de la energía cinética

Para la energía cinética podemos efectuar una descomposición análoga a la del momento cinético. Escribiendo cada velocidad como suma de la del CM más la relativa

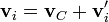
$\mathbf{v}_i = \mathbf{v}_C+\mathbf{v}'_i$

queda, para la energía cinética individual,

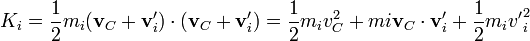
$K_i = \frac{1}{2}m_i(\mathbf{v}_C+\mathbf{v}'_i)\cdot(\mathbf{v}_C+\mathbf{v}'_i) = \frac{1}{2}m_iv_C^2+mi\mathbf{v}_C\cdot\mathbf{v}'_i+\frac{1}{2}m_i{v'}_i^2$

y para la energía cinética total

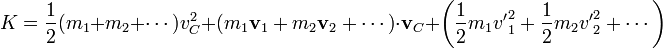
$K = \frac{1}{2}(m_1+m_2+\cdots)v_C^2+\left(m_1\mathbf{v}_1+m_2\mathbf{v}_2+\cdots\right)\cdot\mathbf{v}_C +\left(\frac{1}{2}m_1{v'}_1^2+\frac{1}{2}m_2{v'}^2_2+\cdots\right)$

El segundo término se anula por aparecer en él 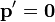$\mathbf{p}'=\mathbf{0}$ , lo que reduce la energía cinética a

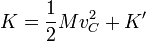
$K = \frac{1}{2}Mv_C^2 + K'$

con

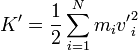
$K' = \frac{1}{2}\sum_{i=1}^N m_i {v'}^2_i$

la energía cinética del sistema relativa al centro de masas.

Esta descomposición se interpreta como que el sistema posee una energía cinética por el movimiento de traslación colectivo, más un término debido al movimiento sobre sí mismo. Esta energía cinética intrínseca, $K'$ es parte de la energía interna del sistema. Puede estar asociada a:

un movimiento organizado. Por ejemplo, en la rotación de la Tierra alrededor de su eje.
un movimiento desorganizado. Por ejemplo, en un gas que se encuentra a una cierta temperatura, el centro de masas puede estar estacionario y sin embargo el gas posee una energía cinética debido al movimiento de las moléculas que lo componen. Esta energía cinética es lo que llamamos agitación térmica.
una combinación de ambos. Este es el caso general. La energía cinética del sistema parte se encuentra en movimientos macroscópicos (rotación o traslación de partes del sistema) y parte en movimientos microscópicos caóticos.

Por la presencia de estos términos microscópicos caóticos la energía cinética total del sistema es normalmente desconocida. En su lugar nos limitamos a la suma del término 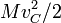$Mv_C^2/2$ con la suma de las energías cinéticas debidas a los movimientos macroscópicos.

3 Leyes de conservación

La utilidad de las definiciones del centro de masa y las propiedades colectivas del sistema se pone de manifiesto cuando se estudia cómo varían en el tiempo y en qué casos son constantes de movimiento.

3.1 De la cantidad de movimiento

Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es

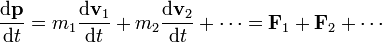
$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = m_1\frac{\mathrm{d}\mathbf{v}_1}{\mathrm{d}t}+ m_2\frac{\mathrm{d}\mathbf{v}_2}{\mathrm{d}t}+\cdots = \mathbf{F}_1+\mathbf{F}_2 + \cdots$

esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas

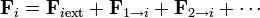
$\mathbf{F}_i = \mathbf{F}_{i\mathrm{ext}}+\mathbf{F}_{1\to i}+\mathbf{F}_{2\to i}+\cdots$

y la derivada de la cantidad de movimiento queda

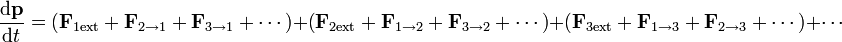
$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\left(\mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\to 1}+\mathbf{F}_{3\to 1}+\cdots\right)+\left(\mathbf{F}_{2\mathrm{ext}}+\mathbf{F}_{1\to 2}+\mathbf{F}_{3\to 2}+\cdots\right)+\left(\mathbf{F}_{3\mathrm{ext}}+\mathbf{F}_{1\to 3}+\mathbf{F}_{2\to 3}+\cdots\right)+\cdots$

Pero, de acuerdo con la tercera ley de Newton

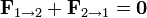
$\mathbf{F}_{1\to 2}+\mathbf{F}_{2\to 1} = \mathbf{0}$

y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil

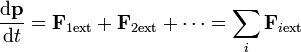
$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}= \mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\mathrm{ext}}+\cdots = \sum_i \mathbf{F}_{i\mathrm{ext}}$

esto es:

la derivada de la cantidad de movimiento es igual a la resultante de las fuerzas externas aplicadas sobre el sistema.
En particular: En ausencia de fuerzas externas, la cantidad de movimiento de un sistema de partículas permanece constante.

En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe

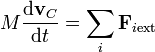
$M\frac{\mathrm{d}\mathbf{v}_C}{\mathrm{d}t} = \sum_i \mathbf{F}_{i\mathrm{ext}}$

es decir:

El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se ecnontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema.

En particular, el centro de masas de un sistema de partículas sometidas exclusivamente a fuerzas internas permanece en reposo o en un estado de movimiento uniforme.

Consideremos el ejemplo siguiente: un proyectil se lanza desde un mortero. El proyectil describe (despreciando la resistencia del aire) una trayectoria parabólica. En cierto punto del vuelo el proyectil explota en multitud de fragmentos. El centro de masas de estos fragmentos continúa el movimiento parabólico inicial.

Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide.

3.2 Del momento angular

Derivando igualmente en la expresión del momento cinético de un sistema de partículas obtenemos

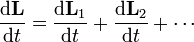
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} = \frac{\mathrm{d}\mathbf{L}_1}{\mathrm{d}t} + \frac{\mathrm{d}\mathbf{L}_2}{\mathrm{d}t} + \cdots$

Para cada partícula la derivada del momento angular es el momento de las fuerzas aplicadas sobre ella:

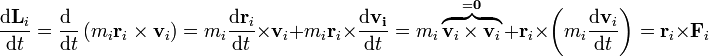
$\frac{\mathrm{d}\mathbf{L}_i}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(m_i\mathbf{r}_i\times\mathbf{v}_i\right) = m_i\frac{\mathrm{d}\mathbf{r}_i}{\mathrm{d}t}\times\mathbf{v}_i + m_i\mathbf{r}_i\times\frac{\mathrm{d}\mathbf{v_i}}{\mathrm{d}t} = m_i\overbrace{\mathbf{v}_i\times\mathbf{v}_i}^{=\mathbf{0}} + \mathbf{r}_i\times\left(m_i\frac{\mathrm{d}\mathbf{v}_i}{\mathrm{d}t}\right) = \mathbf{r}_i\times\mathbf{F}_i$

y, para el momento cinético total

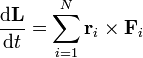
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \sum_{i=1}^N \mathbf{r}_i\times\mathbf{F}_i$

De nuevo, esta expresión requiere conocer las fuerzas internas del sistema, que son usualmente desconocidas. Por ello, descomponemos de nuevo en sumas de fuerzas externas e internas

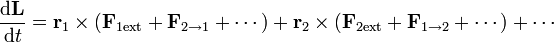
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \mathbf{r}_1\times\left(\mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\to 1}+\cdots\right) + \mathbf{r}_2\times\left(\mathbf{F}_{2\mathrm{ext}}+\mathbf{F}_{1\to 2}+\cdots\right)+ \cdots$

Pero, según dijimos al principio del artículo, si las fuerzas internas entre dos partículas no solo cumplen la tercera ley de Newton, sino que además son centrales, esto es, van en la dirección de la recta que une las dos partículas se verifica

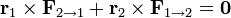
$\mathbf{r}_1\times\mathbf{F}_{2\to 1}+\mathbf{r}_2\times\mathbf{F}_{1\to 2}=\mathbf{0}$

Esta condición se cumple en la mayoría de los casos prácticos (fuerzas eléctricas o gravitatorias). En este caso, los momentos de las fuerzas internas se anulan dos a dos y queda

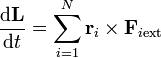
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \sum_{i=1}^N \mathbf{r}_i\times\mathbf{F}_{i\mathrm{ext}}$

En palabras:

La derivada del momento angular o cinético de un sistema de partículas es igual a la suma de los momentos de las fuerzas externas aplicadas sobre el sistema.

En particular, en un sistema de partículas sometido exclusivamente a fuerzas internas, el momento angular permanece constante.

3.3 El caso de la energía cinética

Para la energía cinética no existe un teorema tan simple como para la cantidad de movimiento o el momento cinético. Operando del mismo modo que para estas dos cantidades, en sencillo probar que

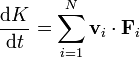
$\frac{\mathrm{d}K}{\mathrm{d}t} = \sum_{i=1}^N \mathbf{v}_i\cdot\mathbf{F}_i$

esto es, la derivada de la energía cinética es la potencia desarrollada por todas las fuerzas ejercidas en el sistema. Sin embargo, en este caso, no podemos eliminar las fuerzas internas de la ecuación. La razón es que las fuerzas internas sí pueden variar la energía cinética total.

Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total.

4 Aplicaciones

4.1 Sistema de dos partículas

4.1.1 Explosión de un proyectil

Supongamos un proyectil de masa $M$ que es disparado con un mortero desde el suelo. Cuando el proyectil lleva recorrida horizontalmente una distancia $a$ y se encuentra en el punto más alto de la parábola, se parte en dos pedazos desiguales. Uno de ellos, de masa $M / 3$ cae justo en la vertical del punto de explosión. El segundo fragmento impacta en el suelo al mismo tiempo que el primero. ¿A qué distancia del primero?

Una forma de resolver esto sería determinar la velocidad del segundo fragmento inmediatamente tras la explosión y estudiar su movimiento parabólíco siguiente, para hallar su alcance, pero no se nos dice ni la velocidad inicial, ni el ángulo con que fue disparado el proyectil.

Lo más sencillo es utilizar que el centro de masas se mueve como una partícula sometida a la resultante de las fuerzas externas, en este caso, el peso total. Por tanto, describe el arco de parábola completo, hasta impactar en el suelo, a una distancia $2 a$ del punto del disparo.

Si el fragmento de masa $M / 3$ se encuentra en $x 1 = a$ y el centro de masas en $x C = 2 a$ , ambos a la altura $y = 0$ , la posición del segundo fragmento la obtenemos de

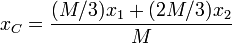
$x_C = \frac{(M/3)x_1+(2M/3)x_2}{M}$ $\Rightarrow$

3 x C = x 1 + 2 x 2

$\Rightarrow$

6 a = a + 2 x 2

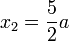
$\Rightarrow$ $x_2 = \frac{5}{2}a$

4.1.2 Dos partículas unidas por un oscilador armónico

Artículo completo: Dos partículas unidas por un oscilador armónico

Supongamos dos partículas de la misma masa $m$ unidas por un resorte de constante $k$ y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad $v 0$ alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?

4.1.3 Dos partículas unidas por una barra

Artículo completo: Dos partículas unidas por una barra

Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que puden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial $v 0$ perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?

5 Colisiones

6 Definición

Una colisión entre dos partículas es una interacción entre dos partículas que ocurre en un espacio limitado y un intervalo de tiempo corto.

Un ejemplo típico es el choque de dos bolas de billar. Durante el breve periodo de colisión, cada partícula se contrae elásticamente una pequeña cantidad, para acto seguido volver a expandirse, saliendo cada bola despedida en la misma dirección o en una dirección diferente. Otro ejemplo similar es el choque de una pelota de tenis contra una raqueta o una superficie rígida. En la imagen vemos una imagen a cámara lenta del choque de una pelota de raquetbol chocando contra una pared (fuente: HSI at NCSSM). Vemos que durante el tiempo de colisión la pelota se deforma enormemente.

Al considerar una colisión no nos interesa tanto el qué ocurre durante la colisión, sino la relación entre el estado de las partículas antes y después de la colisión. Para ello, lo que se utiliza es que las interacciones conservarán la cantidad de movimiento, el momento cinético y, en ciertas ocasiones, la energía cinética.

También es una colisión un péndulo balístico en el cual una bala se empotra en un objeto masivo, comunicándole una cierta velocidad. Aunque la interacción de la bala y el péndulo se puede considerar que continúa tras la colisión (pues ahora forman el mismo sólido), los cambios bruscos de velocidad se producen en un intervalo reducido de tiempo.

No es una colisión una interacción a grandes distancias o que se prolonga durante un periodo largo de tiempo. Por ejemplo, la atracción gravitatoria entre dos masas que orbitan la una alrededor de la otra es un estado permanente y no puede ser considerada una colisión.

El concepto de intervalo de tiempo corto o largo es relativo. La comparación se hace con el intervalo de tiempo en el que estamos considerando el movimiento de la partículas. Por ejemplo, cuando se lanza un satélite a Saturno, la nave se mueve por la atracción gravitatoria solar durante años, por lo que esta atracción no es una colisión. Sin embargo, durante el camino, para acelerar la nave, se puede emplear el método de catapulta gravitatoria, haciéndola pasar junto a Júpiter y ganando energía en el encuentro. Este acercamiento a Júpiter dura algunos días y sí puede ser tratado como una colisión (aunque la nave no llega a “tocar” Júpiter, sólo su campo gravitatorio).

7 Choques unidimensionales

La descripción de una colisión suele hacerse en dos sistemas de referencia diferentes, ambos inerciales. Uno es el llamado sistema laboratorio, que representa a un observador externo al sistema de dos partículas. El otro es el sistema centro de masas (CM), ligado al centro de masas del sistema de dos partículas. En el sistema CM la descipción es más sencilla, pero, dado que las medidas experimentales son realizadas en el sistema laboratorio, el procedimiento habitual es comenzar el estudio en el sistema laboratorio, pasar al sistema centro de masas, analizar la colisión en éste, y luego transformar los resultados de vuelta al sistema laboratorio.

Aquí, por simplicidad, consideraremos solo el choque de dos masas que, tras la colisión, se separan en la misma dirección en la que se acercaron. Esto permite usar cantidades escalares en lugar de vectores.

Suponemos entonces dos partículas, de masas $m 1$ y $m 2$ que se mueven con velocidades iniciales $v 1 i$ y $v 2 i$ , respectivamente. Tras la colisión las velocidades pasarán a ser $v 1 f$ y $v 2 f$

Al ser un problema sencillo, puede prescindirse del sistema CM para determinar el resultado de la colisión.

8 Conservación de la cantidad de movimiento

Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y

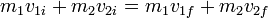
$m_1v_{1i}+m_2v_{2i} = m_1v_{1f} + m_2v_{2f}\,$

Esta es la ecuación básica que gobierna las colisiones.

De que se conserve la cantidad de movimiento se deduce que la velocidad del centro de masas permanece constante

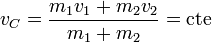
$v_C=\frac{m_1v_1+m_2v_2}{m_1+m_2}=\mathrm{cte}$

Podemos medir las velocidades de cada partícula respecto al CM y obtener las velocidades relativas

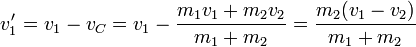
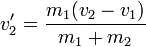
$v'_1 = v_1 - v_C = v_1 - \frac{m_1v_1+m_2v_2}{m_1+m_2} = \frac{m_2(v_1-v_2)}{m_1+m_2}$ $v'_2 = \frac{m_1(v_2-v_1)}{m_1+m_2}$

Estas velocidades relativas verifican la condición

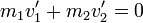
$m_1v'_1+m_2v'_2 = 0\,$

tanto antes como después de la colisión.

9 Conservación de la energía

La energía cinética no se conserva en general en una colisión, sino que suele disiparse parcialmente. Una pelota que rebota en el suelo no vuelve a alcanzar la altura desde la que partió.

Esto quiere decir que habrá una diferencia en la energía cinética debido a la colisión

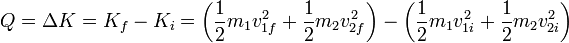
$Q = \Delta K = K_f-K_i = \left(\frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2\right) - \left(\frac{1}{2}m_1v_{1i}^2 + \frac{1}{2}m_2v_{2i}^2\right)$

Esta energía o bien se manifiesta como un aumento de la temperatura de las partículas, o bien se pierde en forma de calor (o un poco de cada cosa).

Dependiendo de la cantidad de energía cinética que se pierda, puede hacerse una clasificación de las colisiones:

Colisión perfectamente elástica: Es aquella en la que no se disipa energía cinética y ésta se conserva.

Colisión inelástica: Aquella en la que se disipa parte de la energía cinética.

Colisión completamente inelástica: Aquella en la que se disipa el máximo de energía. Este máximo no es toda la energía cinética en el sistema laboratorio, ya que la conservación de la cantidad de movimiento impone que el sistema se mueva tras la colisión, y por tanto conserve parte de la energía cinética.

Las colisiones completamente inelásticas se dan cuando los dos partículas se fusionan y continúan su marcha como una sola partícula con masa la suma de las dos originales.

Explosiones: Un proceso que no es estrictamente una colisión, pero que puede ser tratado matemáticamente como una, es el de la explosión. Una sola partícula se descompone en dos (o más) fragmentos, que pasan a moverse por separado. Vendría a ser el opuesto de una colisión completamente inelástica. En este caso la energía cinética del sistema aumenta, normalmente a costa de la energía interna de origen químico.

9.1 Coeficiente de restitución

Para caracterizar el tipo de colisión del que se trata se define un parámetro denominado coeficiente de restitución

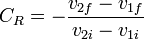
$C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}}$

que en términos geométricos representa la proporción entre la velocidad relativa con la que se alejan las partícula y la velocidad con la que se acercaban. El coeficiente de restitución tiene l mismo valor en el sistema laboratorio que en el sistema centro de masas.

En una colisión perfectamente elástica, $C R = 1$ y las partículas se alejan con la misma velocidad con la que se acercaban.

En una colisión completamente inelástica, $C R = 0$ y las partículas no se alejan tras la colisión.

Para un caso intermedio se tendrá que $0 < C R < 1$ .

10 Colisión perfectamente elástica

Vamos a determinar las velocidades finales en el caso de que se conserve la energía cinética. Para ello debemos resolver el sistema de dos ecuaciones con dos incógnitas

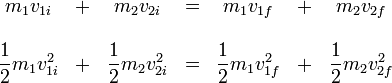
$\begin{array}{ccccccc}m_1v_{1i}&+&m_2v_{2i}&= & m_1v_{1f}&+& m_2v_{2f} \\ && \\ \displaystyle \frac{1}{2}m_1v_{1i}^2&+&\displaystyle\frac{1}{2}m_2v_{2i}^2 & = & \displaystyle \frac{1}{2}m_1v_{1f}^2&+&\displaystyle\frac{1}{2}m_2v_{2f}^2 \end{array}$

que podemos reescribir, reagrupando términos y factorizando

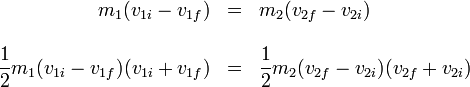
$\begin{array}{rcl}m_1(v_{1i}-v_{1f})&= & m_2(v_{2f}-v_{2i}) \\ && \\ \displaystyle \frac{1}{2}m_1(v_{1i}-v_{1f})(v_{1i}+v_{1f}) & = & \displaystyle \frac{1}{2}m_2(v_{2f}-v_{2i})(v_{2f}+v_{2i}) \end{array}$

Sustituyendo la primera en la segunda llegamos a que efectivamente el coeficiente de restitución es igual a la unidad.

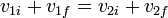
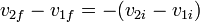
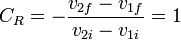
$v_{1i}+v_{1f}=v_{2i}+v_{2f}\,$ $\Rightarrow$ $v_{2f}-v_{1f}=-(v_{2i}-v_{1i})\,$ $\Rightarrow$ $C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}} = 1$

Combinando esta relación la ley de conservación de la cantidad de movimiento tenemos un sistema de dos ecuaciones lienales con dos incógnitas, con solución

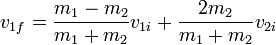
$v_{1f} = \frac{m_1-m_2}{m_1+m_2}v_{1i} + \frac{2m_2}{m_1+m_2}v_{2i}$ $v_{2f} = \frac{2m_1}{m_1+m_2}v_{1i}+\frac{m_2-m_1}{m_1+m_2}v_{2i}$

10.1 Choque de dos masas iguales

Cuna de Newton

Un caso particular importante es aquel en que las dos partículas que colisionan tienen la misma masa. En este caso

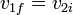
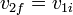
$v_{1f}= v_{2i}\,$ $v_{2f}=v_{1i}\,$

Las dos partículas intercambian sus velocidades. En particular si se trata de una partícula que choca contra una que está en reposo, la primera se queda “clavada”, mientras que la segunda sale con la velocidad que llevaba la primera. Este es un fenómeno común en el billar y la base del dispositivo conocido como cuna de Newton, en el que varias bolas colisionan sucesivamente.

10.2 Caso de un blanco en reposo

Un caso importante entre las colisiones es el representado por una partícula móvil (proyectil) que impacta sobre una fija (blanco).

Matemáticamente la condición es

$v_{1i}=v_0\qquad v_{2i}=0$

lo que nos da las velocidades resultantes

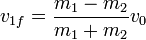
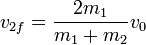
$v_{1f} = \frac{m_1-m_2}{m_1+m_2}v_{0}$ $v_{2f} = \frac{2m_1}{m_1+m_2}v_{0}$

Los resultados dependen de la proporción entre las masas. Si $γ = m 1 / m 2$ queda

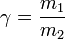
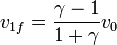
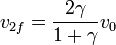
$\gamma=\frac{m_1}{m_2}$ $\Rightarrow$ $v_{1f}=\frac{\gamma-1}{1+\gamma}v_0$ $v_{2f}=\frac{2\gamma}{1+\gamma}v_0$

10.2.1 Blanco masivo

Cuando el blanco es más pesado que el proyectil ( $m 2 > m 1$ , o $γ < 1$ ), $v 1 f$ se hace negativo, lo cual quiere decir que el proyectil rebota.

El caso límite es aquel en que el blanco es infinitamente masivo. Esto corresponde, por ejemplo, al choque de una pelota contra una pared. En este caso

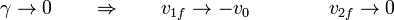
$\gamma\to0\qquad\Rightarrow\qquad v_{1f}\to -v_0\qquad\qquad v_{2f}\to 0$

esto es, el proyectil rebota con la misma velocidad con la que venía. El blanco permanece inmóvil (aunque adquiere la cantidad de movimiento que pierde el proyectil).

10.2.2 Blanco ligero

En el otro extremo tenemos el caso del blanco más ligero que el proyectil (“matar moscas a cañonazos”). En esta caso $γ > 1$ y $v 1 f > 0$ , lo que quiere decir que el proyectil no rebota, sino que continúa hacia adelante, con una velocidad menor que la incidente. El blanco sale despedido con una velocidad mayor que la del proyectil, por lo que se separa de éste.

En el caso límite de proyectil infinitamente masivo (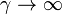 $\gamma\to \infty$ ) el proyectil continúa su camino imperturbado, mientras que el blanco sale disparado con una velocidad doble de la del proyectil

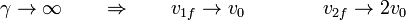
$\gamma\to \infty\qquad\Rightarrow\qquad v_{1f}\to v_0\qquad\qquad v_{2f}\to 2v_0$

Podemos representar los resultados para los dos casos en una gráfica semilogarítmica. A la izquierda tenemos el límite de blanco ligero y a la derecha el de blanco infinitamente pesado. En la posición central tenemos el caso de dos masas iguales.

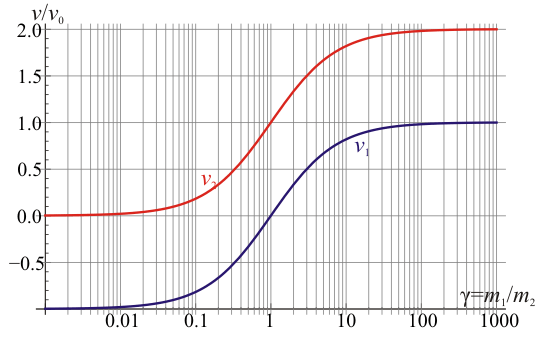
Obtenemos una gráfica diferente si en lugar de representar las velocidades representamos la cantidad de movimiento de cada partícula, comparada con la inicial del proyectil. En este caso tenemos

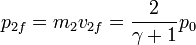
$p_0=m_1v_0\qquad\qquad p_{1f}=m_1v_{1f}=\frac{\gamma -1}{\gamma+1}p_0$ $p_{2f}=m_2v_{2f}=\frac{2}{\gamma+1}p_0$

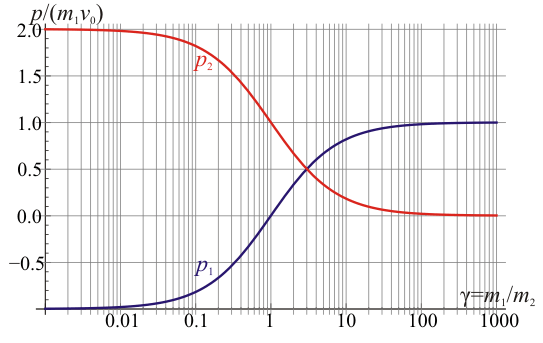
Vemos que, cuando el proyectil es muy ligero comparado con el blanco, éste se lleva el doble de cantidad de movimiento que traía inicilamente el proyectil, pese a que la velocidad del blanco es prácticamente nula (este es es el caso de una pelota que choca con una pared; aunque ésta casi no se mueve, sí se lleva cantidad de movimiento).

También podemos representar la energía cinética de cada partícula, comparada con la inicial.

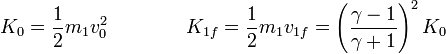
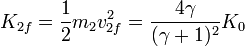
$K_0=\frac{1}{2}m_1v_0^2\qquad\qquad K_{1f}=\frac{1}{2}m_1v_{1f}=\left(\frac{\gamma -1}{\gamma+1}\right)^2K_0$ $K_{2f}=\frac{1}{2}m_2v_{2f}^2=\frac{4\gamma}{(\gamma+1)^2}K_{0}$

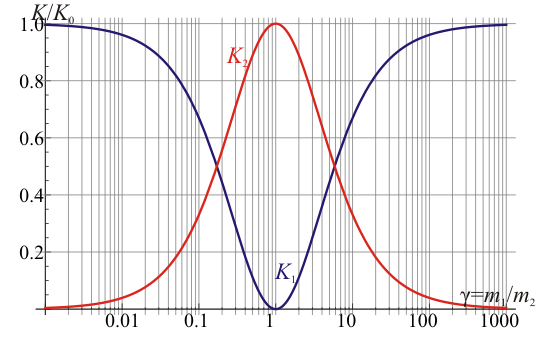
Vemos que, tanto si el proyectil es muy ligero como si es muy pesado la energía con la que sale de la colisión es casi igual a la de entrada, y que el máximo de transferencia de energía al blanco se da cuando las dos masas son iguales (en cuyo caso le cede toda la energía.

11 Colisión completamente inelástica

En el otro extremo en cuanto a la energía cinética se encuentra la colisión completamente inelástica, en la que se disipa el máximo de energía.

Podemos calcular el máximo de energía disipada, descomponiendo la energía cinética en suma de energía cinética del CM, más energía cinética relativa

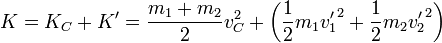
$K = K_C + K' = \frac{m_1+m_2}{2}v_C^2 + \left(\frac{1}{2}m_1{v'_1}^2+\frac{1}{2}m_2{v'_2}^2\right)$

El primer término es constante, por serlo la velocidad del CM. Por ello, el máximo de la energía disipada se dará cuando las velocidades relativas al CM, tras la colisión sean nulas, esto es, cuando las dos partículas resulten con la misma velocidad, que será la del CM,

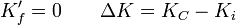
$v'_{1f}=0\qquad v'_{2f}=0$ $\Rightarrow$ $K'_f = 0\qquad \Delta K = K_C - K_i\,$

La velocidad del CM, que será la de la única partícula resultante es

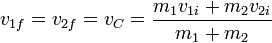
$v_{1f}=v_{2f}=v_C=\frac{m_1v_{1i}+m_2v_{2i}}{m_1+m_2}$

En el caso particular de un proyectil que impacta con un blanco, esta velocidad se reduce a

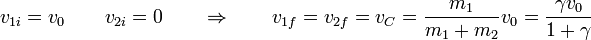
$v_{1i}=v_0\qquad v_{2i}=0\qquad\Rightarrow\qquad v_{1f}=v_{2f}=v_C=\frac{m_1}{m_1+m_2}v_0=\frac{\gamma v_0}{1+\gamma}$

Si el proyectil es muy ligero comparado con el blanco esta velocidad se aproxima a $γ v 0$ . Esto es lo que ocurre en un péndulo balístico; si es mucho más pesado, el proyectil se lleva al blanco por delante y continúa su marcha casi inalterado (como un tren que choca con una mosca estacionaria).

Podemos representar la energía final comparada con la inicial, así como la pérdida relativa de energía

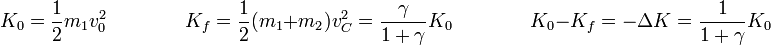
$K_0=\frac{1}{2}m_1v_0^2\qquad\qquad K_f = \frac{1}{2}(m_1+m_2)v_C^2=\frac{\gamma}{1+\gamma}K_0\qquad\qquad K_0-K_f = -\Delta K=\frac{1}{1+\gamma}K_0$

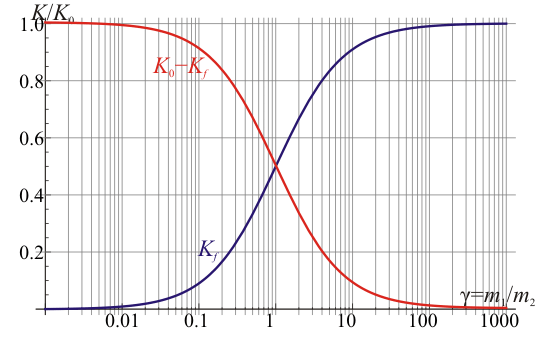
Si el proyectil es muy ligero se pierde casi toda la energía, pero si es muy pesado comparado con el blanco, la energía apenas se disipa.

12 Colisiones en tres dimensiones

El problema general de una colisión de dos partículas en tres dimensiones, cuando la dirección en que se desvían la partículas no coincide con la dirección de movimiento inicial es bastante más complicado y ofrece una gran variedad de casos posibles.

Aquí sólo consideraremos el más simple: el choque perfectamente elástico de dos partículas de la misma masa, cuando una de ellas (el proyectil) impacta sobre la otra (el blanco) que se encuentra estacionaria. Esta es, aproximadamente, la situación que se produce en el billar cuando el impacto no es frontal.

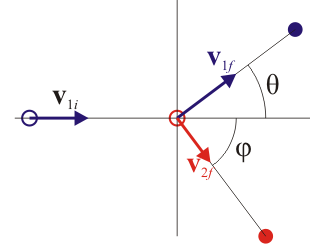
Supondremos un sistema de referencia con origen en en el blanco y con eje X el de incidencia del proyectil, de forma que las velocidades iniciales son

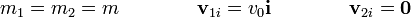
$m_1=m_2=m\qquad\qquad \mathbf{v}_{1i}=v_0\mathbf{i}\qquad\qquad \mathbf{v}_{2i}=\mathbf{0}$

Tras la colisión, la partícula 1 se desvía en un ángulo $θ$ , mientras que la 2 lo hace un ángulo $\varphi$ hacia el otro lado, por lo que las velocidades finales son

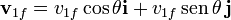
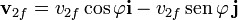
$\mathbf{v}_{1f}=v_{1f}\cos\theta\mathbf{i}+v_{1f}\,\mathrm{sen}\,\theta\,\mathbf{j}$ $\mathbf{v}_{2f}=v_{2f}\cos\varphi\mathbf{i}-v_{2f}\,\mathrm{sen}\,\varphi\,\mathbf{j}$

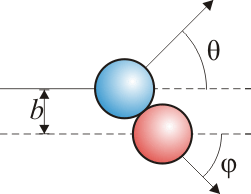
Cuando se trata de partículas puntuales, el ángulo $θ$ queda indeterminado y hay que darlo como un dato adicional del problema. Para sólidos reales, como esferas, el ángulo $θ$ lo determina el que las esferas no incidan centralmente, sino a una cierta distancia del centro (denominada habitualmente parámetro de impacto, $b$ ).

La conservación de la cantidad de movimiento impone que

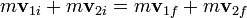
$m\mathbf{v}_{1i}+m\mathbf{v}_{2i}=m\mathbf{v}_{1f}+m\mathbf{v}_{2f}\,$

Dividiendo por la masa y sustituyendo las velocidades iniciales

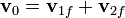
$\mathbf{v}_0=\mathbf{v}_{1f}+\mathbf{v}_{2f}$

La conservación de la energía implica

Al ser la colisión elástica, también se conserva la energía cinética, por lo que

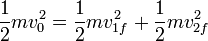
$\frac{1}{2}mv_0^2 = \frac{1}{2}mv_{1f}^2+\frac{1}{2}mv_{2f}^2$

Multiplicando por $2 / m$

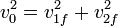
$v_0^2 = v_{1f}^2+v_{2f}^2$

Si multiplicamos escalarmente la conservación del momento por sí misma

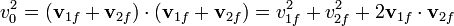
$v^2_0=(\mathbf{v}_{1f}+\mathbf{v}_{2f})\cdot(\mathbf{v}_{1f}+\mathbf{v}_{2f})=v^2_{1f}+v^2_{2f}+2\mathbf{v}_{1f}\cdot\mathbf{v}_{2f}$

Restando la ley de conservación de la energía llegamos a la condición

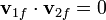
$\mathbf{v}_{1f}\cdot\mathbf{v}_{2f}=0$

que implica que las partículas se separan siguiendo trayectorias ortogonales (o bien una de las dos partículas se queda inmóvil tras la colisión). En términos de los ángulos

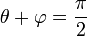
$\theta+\varphi=\frac{\pi}{2}$

En cuanto a la celeridad con la que se aleja cada una, depende del ángulo de desviación. Por la ortogonalidad tenemos

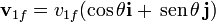
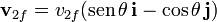
$\mathbf{v}_{1f}=v_{1f}(\cos\theta\mathbf{i}+\,\mathrm{sen}\,\theta\,\mathbf{j})$ $\mathbf{v}_{2f}=v_{2f}(\mathrm{sen}\,\theta\,\mathbf{i}-\cos\theta\,\mathbf{j})$

Sustituyendo en la conservación de la cantidad de movimiento e igualando componente a componente quedan las ecuaciones

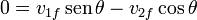
$v_0 = v_{1f}\cos\theta+v_{2f}\,\mathrm{sen}\,\theta$ $0 = v_{1f}\,\mathrm{sen}\,\theta-v_{2f}\cos\theta$

de donde

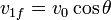
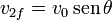
$v_{1f}=v_0\cos\theta\,$ $v_{2f}=v_0\,\mathrm{sen}\,\theta$

siendo las energías cinéticas resultantes

$K_{1f}=K_0\cos^2\theta\qquad\qquad K_{2f}=K_0\,\mathrm{sen}^2\theta$

Para un ángulo de desviación $θ = 0$ , el proyectil se lleva toda la energía y el blanco se queda parado. realmente en este caso no hay colisión.

Si el ángulo de desviación es el máximo posible $θ = π / 2$ , el proyectil se queda parado y el blanco se aleja en la misma dirección. Este es de nuevo el caso unidimensional que ya conocemos.

Para $π / 4$ las dos partículas se reparten la energía a partes iguales y se marchan en direcciones simétricas respecto a la línea de incidencia.