Problemas de introducción a la física (GIE)
De Laplace
Revisión a fecha de 22:43 22 sep 2011; Antonio (Discusión | contribuciones)
1 Ejemplos de valores numéricos
Las siguientes cantidades representan aproximadamente los valores de las magnitudes de la tabla, expresadas en las unidades fundamentales del SI o productos de ellas. Indique cuál le corresponde a cada una, indicando sus unidades.
| 1 | Peso de una persona | 2 | Densidad de masa del agua | 3 | Aceleración de la Tierra alrededor del Sol |
| 4 | Masa de la Tierra | 5 | Diámetro de un glóbulo rojo | 6 | Distancia Tierra-Sol |
| 7 | Altura a la que se encuentra la Estación Espacial Internacional | 8 | Radio de un átomo | 9 | Densidad del oro |
| 10 | Diámetro de una pelota de golf | 11 | Espesor de un folio | 12 | Aceleración de la gravedad |
| 13 | Volumen aproximado de oro en la Tierra | 14 | Velocidad de Usain Bolt en los 100m | 15 | Masa de un m³ de agua |
| 16 | Duración de un año | 17 | Velocidad de una bacteria | 18 | Periodo de la corriente alterna doméstica |
| 19 | Masa del electrón | 20 | Velocidad de la luz | 21 | Circunferencia terrestre |
| A | 10−30 | B | 10−10 | C | 6×10−6 |
| D | 5×10−5 | E | 6×10−3 | F | 2×10−2 |
| G | 5×10−2 | H | 10−1 | I | 10 |
| J | 10 | K | 8× 102 | L | 103 |
| M | 103 | N | 103 | O | 6×104 |
| P | 2×104 | Q | 5×105 | R | 3×107 |
| S | 4×107 | T | 3× 108 | U | 1.5×1011 |
2 Ejemplos de cálculo de dimensiones
A partir de las relaciones definitorias
| Velocidad | Cantidad de movimiento | Aceleración | Fuerza |
|---|---|---|---|
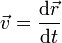
| 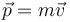
| 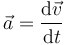
| 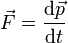
|
| Trabajo | Potencia | Momento cinético | Momento de una fuerza |
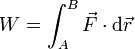
| 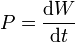
| 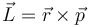
| 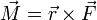
|
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades fundamentales de este sistema.





