Entrar Página Discusión Historial Go to the site toolbox

Cinemática de la partícula (GIE)

De Laplace

Contenido

1 En una dimensión

  1. Posición
  2. Velocidad
    1. Media
    2. Instantánea
  3. Aceleración
  4. Ejemplos de movimiento
    1. Uniforme
    2. Uniformemente acelerado
    3. Armónico simple

2 En dos y tres dimensiones

  1. Vector de posición
  2. Velocidad
    1. Definición
    2. Rapidez o celeridad
    3. Dirección y sentido. Vector tangente
    4. Distancia recorrida
  3. Aceleración
    1. Definición
    2. Componentes cartesianas
    3. Componentes intrínsecas
      1. Aceleración tangencial
      2. Aceleración normal. Vector normal
  4. Ejemplos de movimiento tridimensional
    1. Rectilíneo
    2. Circular
    3. Parabólico
    4. Helicoidal

3 Introducción

3.1 Cinemática y dinámica

Se dice que un cuerpo se halla en movimiento respecto a otro cuando existe un cambio continuo de su posición relativa a lo largo del tiempo. La rama de la Física que se dedica al estudio del movimiento de los cuerpos es la Mecánica, y ésta se subdivide en las siguientes disciplinas:

Cinemática
que describe geométricamente el movimiento sin atender a sus causas.
Dinámica
que conecta el movimiento y sus características con las causas (fuerzas) que lo producen.
Estática
que establece las condiciones de equilibrio mecánico (ausencia de movimiento).

En este tema nos ocuparemos de la cinemática en general, y de la cinemática de la partícula (o del punto material) específicamente.

Esta descripción se centra en la evolución de las posiciones de las partes de un sistema, como función del tiempo. No requiere el conocimiento de otras cantidades como la masa, la fuerza, o la energía, que son objeto de la Dinámica.

Para poder desarrollar la Cinemática es necesario establecer una serie de conceptos previos, que permitan sostener todo el entramado matemático. Entre estos postulados están

  • Espacio
  • Tiempo
  • Partícula (o punto material)
  • Sólido rígido

3.2 Espacio y tiempo

El espacio y el tiempo son conceptos primitivos, que no pueden definirse más que por la experiencia: el espacio es lo que miden las reglas y el tiempo lo que miden los relojes.

Conjuntamente constituyen el espacio-tiempo, que es el marco en que se produce el movimiento.

No obstante, a la hora de caracterizarlos matemáticamente, es necesario hacer algunas precisiones sobre el modelo que vamos a emplear para describir el movimiento de las partículas.

Independencia entre espacio y tiempo
Dado que no vamos a considerar mecánica relativista, admitiremos que el espacio y el tiempo son magnitudes independientes, medidas separadamente. Es lo que se conoce como espacio-tiempo galileano.
Tiempo uniforme
Admitimos que el tiempo fluye uniformemente y es el mismo para todos los observadores, de forma que si dos eventos son simultáneos para un observador, lo son para todos los demás observadores (esto deja de ser cierto en relatividad).
Espacio euclídeo
Admitimos que el espacio es
  • Homogéneo: posee las mismas propiedades en todos sus puntos.
  • Isótropo: todas las direcciones son equivalentes
  • Tridimensional: Existen tres dimensiones, que podemos denominar largo, ancho y alto.
  • Plano: que no significa que sea bidimensional, sino que cualquier recta puede prolongarse indefinidamente, manteniendo constante su dirección.

Todas estas propiedades son abstracciones, que no resultan de forma inmediata de nuestra experiencia. En la mayoría de los problemas de mecánica, el espacio con el que se trata no es ni homogéneo (no es lo mismo estar sobre el suelo que bajo él), ni isótropo (pues hay una dirección preferida, la dada por la gravedad), ni tridimensional (si se trata de una partícula que rueda por la superficie terrestre), ni plano (por ser curvada la superficie terrestre). Es a base de generalizaciones y abstracciones que se llega al modelo del espacio euclídeo.

3.3 Sistemas de referencia

Todo movimiento se produce respecto a un observador, el cual para describirlo emplea un sistema de referencia. Las propiedades del espacio enunciadas anteriormente permiten que este sistema de referencia sea cartesiano.

Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), x, y, z a estos planos coordenados (x la distancia al YZ, y al XZ, y z al XY).

Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas X, Y y Z. Los vectores unitarios tangentes a estos ejes forman una base ortonormal \{\vec{\imath},\vec{\jmath},\vec{k}\}, conocida como base canónica, de forma que la posición de cualquier punto P puede expresarse mediante su vector de posición

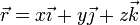
\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}

Un sistema de referencia estará siempre en reposo respecto a sí mismo, pero para otro observador puede estarse moviendo de forma arbitraria. No hay que pensar que un sistema de ejes es algo inmóvil, absoluto y de algún modo ligado al espacio. Un sistema de referencia no es más que una herramienta útil para describir los movimientos y según las circunstancias pueden tomarse ejes que (vistos por otro observador) están rotando o trasladándose.

Por la misma razón no hay que presuponer que, por ejemplo, “el eje Z es vertical”. Nadie se encuentra un eje Z por la calle. El eje Z será el que nosotros queramos que sea y si nos interesa que forme un ángulo de 37° respecto al suelo, pues así lo podemos tomar.

En lo que sigue, siempre que se hable de que una partícula está en reposo o se mueve de tal o cual manera, debe sobreentenderse siempre la coletilla “respecto a un cierto sistema de referencia”, que se fija de antemano.

3.4 Partícula

La partícula o punto material es un modelo matemático consistente en un punto geométrico (sin dimensiones) dotado de una masa finita y distinta de cero (densidad másica infinita). La utilidad de este modelo radica en que:

  • proporciona un punto de partida relativamente simple para el desarrollo teórico de la mecánica de modelos más complejos;
  • aproxima el comportamiento dinámico de aquellos cuerpos cuyas dimensiones propias son muy inferiores a las dimensiones promedio de sus desplazamientos (por ejemplo, los cuerpos celestes);
  • permite estudiar el movimiento del centro de masa de cualquier sistema mecánico.

4 Trayectoria y ley horaria

4.1 Posición instantánea

Cuando una partícula se mueve por el espacio en cada instante ocupará una posición, que irá cambiando de forma continua con el tiempo (ya que la partícula no puede desmaterializarse o teleportarse a otra posición).

En principio podemos etiquetar cada posición por una letra A, B, C,... Sin embargo, es más práctico identificar cada posición por su vector de posición cuyas componentes cartesianas son las distancias (con signo) a los planos coordenados

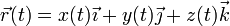
\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}

Aquí x(t), y(t) y z(t) son ciertas funciones continuas del tiempo.

Cuando se da la posición de la partícula como función del tiempo se dice que se conocen las ecuaciones horarias del movimiento.

4.2 Desplazamiento

El desplazamiento de una partícula en un intervalo Δt es la diferencia (vectorial) entre la posición al final del intervalo y la posición inicial

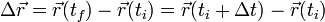
\Delta \vec{r}= \vec{r}(t_f)-\vec{r}(t_i)=\vec{r}(t_i+\Delta t)-\vec{r}(t_i)

Es importante hacer la distinción entre el desplazamiento y la distancia recorrida. Una partícula que recorra una curva cerrada tendrá un desplazamiento nulo, aunque la distancia recorrida no sea nula.

4.3 Desplazamiento diferencial

Cuando tenemos un desplazamiento entre dos instantes muy próximos,separados un intervalo dt, se dice que tenemos un desplazamiento diferencial

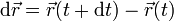
\mathrm{d}\vec{r}=\vec{r}(t+\mathrm{d}t)-\vec{r}(t)

Desde el punto de vista matemático, la palabra diferencial implica el proceso de tomar el límite 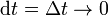\mathrm{d}t = \Delta t\to 0, con lo que técnicamente un desplazamiento diferencial tiene longitud nula. Sin embargo, desde el punto de vista práctico, es más sencillo considerar un desplazamiento diferencial como de longitud muy pequeña comparada con las distancias típicas consideradas. Por ejemplo, si estamos hablando del desplazamiento de un vehículo sobre distancias de kilómetros a lo largo de minutos, un intervalo de milisegundos puede tratarse como un diferencial de tiempo, y un desplazamiento de milímetros puede considerarse un desplazamiento diferencial.

4.4 Trayectoria

Una partícula, al evolucionar en el tiempo, salvo cuando se encuentre en reposo, describe una curva en el espacio. Esta curva se conoce como la trayectoria de la partícula. Las ecuaciones horarias sirven como ecuaciones paramétricas de la trayectoria, siendo el tiempo el parámetro.

No obstante, a una misma trayectoria le pueden corresponder infinitas ecuaciones horarias, dependiendo del ritmo con el que se recorre la curva. Por ejemplo, las ecuaciones horarias

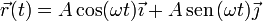
\vec{r}(t) = A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}\,(\omega t)\vec{\jmath}

y

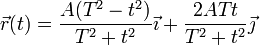
\vec{r}(t) = \frac{A(T^2-t^2)}{T^2+t^2}\vec{\imath}+\frac{2ATt}{T^2+t^2}\vec{\jmath}

corresponden a la misma trayectoria, una circunferencia horizontal.

En ocasiones, para indicar la trayectoria es preferible usar ecuaciones implícitas. En estas, se dan dos funciones (una sola, si el movimiento es plano), tales que

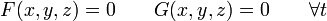
F(x,y,z) = 0\qquad G(x,y,z) = 0\qquad \forall t

Así, los dos ejemplos anteriores verifican

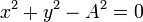
x^2 + y^2 - A^2 = 0\,        z=0\,

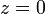
4.5 Parametrización de una trayectoria

La trayectoria que sigue una partícula es una propiedad puramente geométrica, independiente de si se recorre con una cierta velocidad u otra diferente. Por ello, para describir la trayectoria, considerada como curva en el espacio, no es preciso -ni siquiera conveniente- que en esta descripción aparezca explícitamente el tiempo. Todo lo que necesitamos es un método para identificar los puntos que componen la trayectoria.

Esto se consigue mediante una parametrización, que no es más que la asignación de etiquetas individuales para cada punto. Por conveniencia de cálculo, esta etiqueta consiste usualmente en una variable θ, que varía de forma continua a lo largo de la curva.

Por ejemplo, para parametrizar una trayectoria circular, la variable más cómoda es el ángulo que forma el vector de posición con un eje fijo

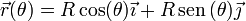
\vec{r}(\theta)=R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}\,(\theta)\vec{\jmath}

y no es necesario interpretar θ en términos de un tiempo (aunque puede hacerse, para visualizar la curva, al variar θ de forma uniforme, recorremos la circunferencia con rapidez constante).

4.6 Parametrización natural

Para evitar el problema que supone identificar si las trayectorias de diferentes movimientos son coincidentes o no (debido a las diferencias en el ritmo con el que se recorre, o las variables empleadas para describir la trayectoria) se introduce la parametrización natural única para cada trayectoria (salvo un signo).

La idea es sencilla. En lugar de etiquetar cada punto de la trayectoria con el instante en que se pasa por él o con una variable arbitraria, se etiqueta usando la distancia s (sobre la curva) desde un punto de referencia:

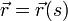
\vec{r}=\vec{r}(s)

Esto es exactamente lo que se hace en las carreteras, cuyos puntos se identifican mediante los postes kilométricos (y no por la hora en que un viajero concreto pase por cada punto).

La parametrización natural es única para cada trayectoria, salvo el signo correspondiente al sentido en que se recorre la curva (en el caso de la carretera, si desde Sevilla a Granada, o desde Granada a Sevilla). También el punto desde el que se empieza a contar queda libre.

A la variable s, que mide la distancia sobre la curva, se la denomina parámetro natural o parámetro arco. Para medir la distancia a lo largo de la curva lo que se hace es rectificar esta. Rectificar consiste en descomponer la curva en una infinitud de trozos de longitud diferencial, cada uno de los cuales se puede considerar aproximadamente rectilíneo, de forma que

\mathrm{d}s=|\mathrm{d}\vec{r}|
            

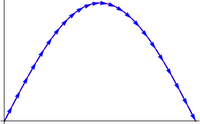
Sumando las longitudes de muchos trocitos diferenciales (esto es, integrando), obtenemos el valor del parámetro arco en un punto de la curva

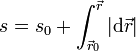
s = s_0+\int_{\vec{r}_0}^\vec{r} |\mathrm{d}\vec{r}|

5 Ley horaria

Cuando se tiene la trayectoria parametrizada en términos de la distancia medida sobre la curva la descripción se completa indicando cómo cambia esta variable con el tiempo. Esta dependencia temporal se conoce como ley horaria:

s = s(t)\,

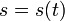
En el ejemplo de un coche que va de Sevilla a Granada, la ley horaria sería la hora a la que pasó por cada punto del camino sin prestar atención si en ese punto en concreto la carretera va hacia el sur o hacia el este.

Según esto, las ecuaciones horarias del movimiento pueden descomponerse en la trayectoria por un lado y la ley horaria por otro:

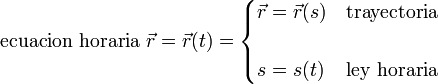
\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(s) & \mbox{trayectoria}\\ & \\ s=s(t)& \mbox{ley horaria}\end{cases}

Si en lugar del parámetro arco, se describe la trayectoria con otra variable, como el ángulo del ejemplo anterior, también se denomina ley horaria a la dependencia de esta variable con el tiempo. Así, en general:

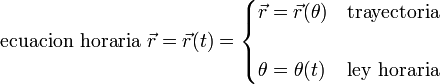
\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(\theta) & \mbox{trayectoria}\\ & \\ \theta=\theta(t)& \mbox{ley horaria}\end{cases}

6 Velocidad

6.1 Velocidad media

Se define la velocidad media como el cociente entre el desplazamiento en un intervalo de tiempo y la duración de dicho intervalo

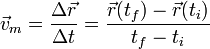
\vec{v}_m = \frac{\Delta \vec{r}}{\Delta t} = \frac{\vec{r}(t_f)-\vec{r}(t_i)}{t_f-t_i}

De la definición se desprende que:

  • La velocidad es un vector: posee dirección y sentido, no solo un módulo (por tanto, decir que la velocidad es de 120 km/h es una información incompleta).
  • Posee unidades de distancia dividida por tiempo, que en el sistema internacional serán m/s.
  • La velocidad media depende del desplazamiento neto entre dos puntos, por tanto en un movimiento cíclico la velocidad media es nula, pues el punto final e inicial coinciden, independientemente de la distancia que se haya recorrido.
  • La velocidad no es igual a espacio partido por tiempo, sino a un desplazamiento dividido por un intervalo, esto es, lo que cuenta no es el valor absoluto de la distancia o la hora que marca el reloj, sino cuánto ha cambiado la posición y cuánto tiempo se ha empleado en realizar dicho desplazamiento.

6.2 Velocidad instantánea

El concepto de velocidad media no es especialmente útil, ya que solo nos informa del ritmo promedio, pero un movimiento concreto puede hacerse de forma irregular y normalmente interesa definir la velocidad en un momento dado, conocida como velocidad instantánea.

Consideremos un movimiento rectilíneo. Cuando decimos que en un instante dado la velocidad es de 120 km/h, ¿qué estamos diciendo exactamente? Evidentemente, no que durante la última hora se han recorrido 120 km, ya que igual sólo se llevan 10 minutos de marcha. Podríamos decir que durante el último minuto se han recorrido 2 km. ya que

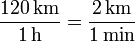
\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}

Esto ya es más preciso, pero aun no es del todo satisfactorio, ya que en un minuto hay tiempo suficiente a acelerar o frenar. Una mejor aproximación sería afirmar que en el último segundo se ha recorrido (1/30) km = 33.3 m. O podríamos decir que en la última décima de segundo se han recorrido 3.33 m,…

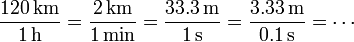
\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}= \frac{33.3\,\mathrm{m}}{1\,\mathrm{s}}=\frac{3.33\,\mathrm{m}}{0.1\,\mathrm{s}}=\cdots

En todos los casos la velocidad es de 120 km/h, pero cuanto más pequeño es el intervalo de tiempo considerado, más nos acercamos al ideal de medir la velocidad en un instante dado.

Definimos entonces la velocidad instantánea como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero (se reduce a un instante)

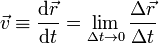
\vec{v}\equiv\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{r}}{\Delta t}

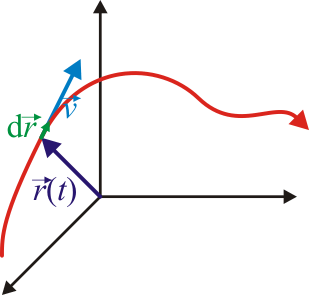
Matemáticamente, esto quiere decir que la velocidad instantánea es la derivada respecto al tiempo del vector de posición. En mecánica, una derivada respecto al tiempo suele representarse con un punto sobre la magnitud

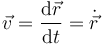
\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \dot{\vec{r}}

De esta definición se deduce que:

  • La velocidad instantánea es un vector: posee módulo, dirección y sentido.
  • Las unidades de la velocidad instantánea son la de una distancia dividida por un tiempo, en el SI m/s, aunque otras unidades como km/h son de uso frecuente.
  • La velocidad instantánea es un vector tangente a la trayectoria en cada punto.

6.3 Celeridad (o rapidez)

6.3.1 Definición

En numerosas ocasiones no estamos interesados en la dirección y sentido de la velocidad, ya que sabiendo que es tangente a la trayectoria, podemos determinarlos geométricamente. En ese caso, la información necesaria se reduce al módulo de la velocidad. A esta cantidad se la conoce como celeridad (o rapidez):

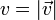
v = \left|\vec{v}\right|

Lo que en el habla cotidiana se denomina velocidad (“iba a 180 km/h”) es realmente una celeridad. Cuando la dirección y el sentido se dan por supuestos, la confusión entre los dos términos no es especialmente grave, pero siempre hay que tener en mente que la velocidad es realmente un vector, no un escalar.

Movimiento uniforme
La celeridad es la cantidad que nos informa del ritmo con el que se recorre la trayectoria. En particular, cuando la trayectoria (cualquiera que ésta sea) se recorre con rapidez constante, el movimiento se denomina movimiento uniforme.
Así, por ejemplo, un movimiento circular uniforme no es un movimiento a velocidad constante, ya que aunque su módulo no varíe, su dirección y sentido cambian a lo largo de la trayectoria.

6.3.2 Unidades

La celeridad posee unidades de una distancia dividida por un tiempo. La unidad SI es el m/s, aunque otras unidades son de uso frecuente:

m/s km/h mph nudos
1 m/s = 1 3.600 2.2369 1.9438
1 km/h = 0.2778 1 0.6214 0.5400
1 mph = 0.4470 1.6093 1 0.8690
1 nudo = 0.5144 1.8520 1.1508 1

Otra rapidez de uso frecuente en Física es la velocidad de la luz

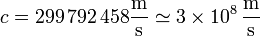
c = 299\,792\,458 \frac{\mathrm{m}}{\mathrm{s}} \simeq 3\times 10^8\,\frac{\mathrm{m}}{\mathrm{s}}

de forma que la celeridad de una partícula elemental suele expresarse como, por ejemplo, v = 0.01c, con lo que la velocidad de la luz funciona también como unidad de medida de velocidades

6.3.3 Relación con la parametrización natural

La celeridad equivale a la velocidad con la que se recorre la distancia medida a lo largo de la curva

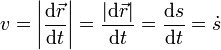
v = \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right| = \frac{|\mathrm{d}\vec{r}|}{\mathrm{d}t} = \frac{\mathrm{d}s}{\mathrm{d}t}=\dot{s}

Esto quiere decir que, si conocemos la rapidez a lo largo de un movimiento, podemos determinar la distancia recorrida hasta un instante dado

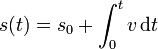
s(t) = s_0 + \int_0^t v\,\mathrm{d}t

Si partimos de la ecuación de la trayectoria en función de una variable cualquiera θ, aunque no represente físicamente a un tiempo, simplemente debemos sustituir la celeridad por el módulo de la derivada respecto a dicho parámetro

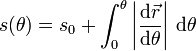
s(\theta) = s_0 + \int_0^{\theta} \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|\,\mathrm{d}\theta

Si podemos invertir una de estas relaciones y hallar el instante en que se llega a una distancia dada, t = t(s) (o θ = θ(s)) entonces podemos usar esta relación para escribir la curva mediante su parametrización natural

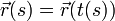
\vec{r}(s) = \vec{r}(t(s))

Puesto que tanto la posición instantánea como el parámetro arco son magnitudes geométricas, esta ecuación de la trayectoria es independiente de la rapidez con la que se describe el movimiento.

En muy contados casos es posible despejar t = t(s). Entre los que sí es posible están el movimiento circular, el helicoidal y el cicloidal.

6.3.3.1 Ejemplo: movimiento circular uniforme

Como ilustración supongamos el movimiento circular

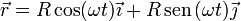
\vec{r}=R\cos(\omega t)\vec{\imath} + R\,\mathrm{sen}\,(\omega t)\vec{\jmath}

La celeridad la calculamos como el módulo de la velocidad

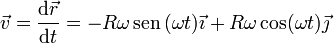
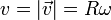
\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}= -R\omega\,\mathrm{sen}\,(\omega t)\vec{\imath}+R\omega\cos(\omega t)\vec{\jmath}   \Rightarrow   v=|\vec{v}|=R\omega\,

El parámetro arco es entonces, suponiendo que empezamos a medir desde t = 0

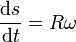
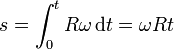
\frac{\mathrm{d}s}{\mathrm{d}t}=R\omega   \Rightarrow    s =\int_0^t R\omega\,\mathrm{d}t = \omega R t

Invirtiendo esta relación

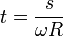
t = \frac{s}{\omega R}

lo que nos da la parametrización natural de la circunferencia

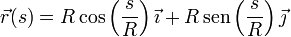
\vec{r}(s)=R\cos\left(\frac{s}{R}\right)\vec{\imath}+R\,\mathrm{sen}\left(\frac{s}{R}\right)\vec{\jmath}

6.4 Celeridad media

La celeridad media de un movimiento en un intervalo es igual al cociente entre la distancia recorrida en dicho intervalo y su duración

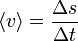
\langle v \rangle = \frac{\Delta s}{\Delta t}

Esta es la cantidad que se usa en el habla coloquial al referirse a la “velocidad media” (“hizo un promedio de 110 km/h”).

Hay que destacar que la celeridad media no es igual al módulo de la velocidad media.

Consideremos un piloto de Fórmula 1 que recorre los 300 km de una carrera en 1:30 h, llegando finalmente a la meta. En ese caso su celeridad media es 200 km/h, pero su velocidad media es nula (pues no hay desplazamiento; acaba donde empezó).

7 Aceleración

7.1 Definición

Del mismo modo que se define la velocidad como la derivada de la posición respecto al tiempo, se define la aceleración instantánea como la derivada de la velocidad respecto al tiempo

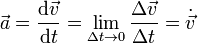
\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{v}}{\Delta t}=\dot{\vec{v}}

Esto quiere decir que la aceleración es la segunda derivada del vector de posición respecto al tiempo, lo que se indica con dos puntos sobre la magnitud

\vec{a}=\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}=\ddot{\vec{r}}

7.2 Unidades

La aceleración tiene unidades de velocidad dividida por tiempo, que en el SI será (m/s)/s = m/s².

Una magnitud con dimensiones de aceleración que es especialmente importante es la aceleración de la gravedad en la superficie terrestre, cuyo valor estándar es, por definición,

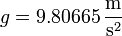
g = 9.80665\,\frac{\mathrm{m}}{\mathrm{s}^2}

de manera que muchas aceleraciones se expresan como múltiplos de esta unidad, aunque dichas aceleraciones no estén relacionadas con la gravedad. Así, por ejemplo, para medir las aceleraciones laterales de un piloto de Fórmula 1 en una curva se dice, por ejemplo, “está sometido a 3 fuerzas G”, que quiere decir que

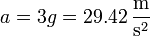
a = 3g = 29.42\,\frac{\mathrm{m}}{\mathrm{s}^2}

Por tanto, g aquí funciona como unidad de medida de la aceleración.

8 Componentes intrínsecas

8.1 Velocidad. Vector tangente

De la definición de velocidad se deduce que se trata de un vector siempre tangente a la trayectoria, ya que un desplazamiento infinitesimal a lo largo de la trayectoria es un vector en la dirección de esta. Esto nos permite definir un vector unitario tangente a la trayectoria normalizando la velocidad

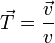
\vec{T}=\frac{\vec{v}}{v}

o, dicho de otra forma

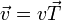
\vec{v}=v\vec{T}

La velocidad instantánea es un vector. La información sobre el módulo se recoge en la celeridad, mientras que la dirección y el sentido los da el vector unitario tangente a la trayectoria.

Puede demostrarse que el vector unitario tangente es independiente de la rapidez, esto es, que da igual que la trayectoria se recorra rápido o lento, el unitario tangente resultante es el mismo. Depende exclusivamente de la geometría de la trayectoria.

La única ambigüedad posible es el sentido. Dado que una misma curva puede recorrerse en un sentido o en el opuesto, existen dos posibles orientaciones para el vector tangente. Para un movimiento dado el unitario tangente siempre apunta en el sentido de avance de la partícula.

8.2 Aceleración

A diferencia de la velocidad, la aceleración puede formar un ángulo cualquiera con la trayectoria.

Podemos escribir entonces el vector aceleración como suma de dos componentes, una en la dirección de movimiento, tangente a la velocidad, y un resto perpendicular a ella. Estas dos componentes se denominan aceleración tangencial y aceleración normal. Estas son las denominadas componentes intrínsecas de la aceleración.

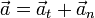
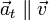
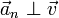
\vec{a}=\vec{a}_t+\vec{a}_n\,        \vec{a}_t\parallel\vec{v}        \vec{a}_n\perp\vec{v}

Hay que destacar que la aceleración tangencial y la normal son vectores, no cantidades escalares. No obstante, también se denominan usualmente de la misma manera a las componentes escalares, dado por supuesto la dirección y el sentido.

Podemos obtener una expresión para la aceleración tangencial proyectando la aceleración sobre el vector tangente, unitario en la dirección de la velocidad

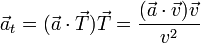
\vec{a}_t = (\vec{a}\cdot\vec{T})\vec{T} = \frac{(\vec{a}\cdot\vec{v})\vec{v}}{v^2}

Conocida la aceleración y calculada la aceleración tangencial, podemos hallar la aceleración normal simplemente restando

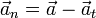
\vec{a}_n = \vec{a}-\vec{a}_t

o bien directamente multiplicando vectorialmente dos veces por el vector velocidad

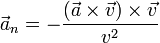
\vec{a}_n = -\frac{(\vec{a}\times\vec{v})\times\vec{v}}{v^2}

8.2.1 Vector normal

A partir de la aceleración normal podemos definir un vector normal a la trayectoria

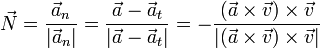
\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=\frac{\vec{a}-\vec{a}_t}{|\vec{a}-\vec{a}_t|}=-\frac{(\vec{a}\times\vec{v})\times\vec{v}}{|(\vec{a}\times\vec{v})\times\vec{v}|}

Como el vector unitario tangente, el unitario normal es una propiedad puramente geométrica y no depende de la rapidez con que se recorra la trayectoria.

8.3 Interpretación de las componentes intrínsecas

Podemos dar una interpretación física de la aceleración tangencial y de la normal, además de la puramente geométrica. Para ello derivamos respecto la tiempo la expresión de la velocidad en función de la celeridad y el vector tangente

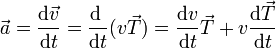
\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}(v\vec{T}) = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{T}+v\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}

El primer término apunta en la dirección tangencial. Podemos demostrar que el segundo es perpendicular a ella, por el ser el vector tangente de módulo constante

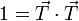
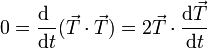
1 = \vec{T}\cdot\vec{T}   \Rightarrow   0=\frac{\mathrm{d}\ }{\mathrm{d}t}(\vec{T}\cdot\vec{T})=2\vec{T}\cdot\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}

Puesto que el producto escalar es nulo, ambos vectores son perpendiculares. En consecuencia

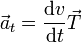
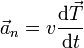
\vec{a}_t = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{T}        \vec{a}_n = v\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}

Por tanto:

Aceleración tangencial
Mide la variación en la celeridad, esto es, si la partícula pasa a moverse más rápido o más lento a lo largo de la trayectoria. La condición para que un movimiento sea uniforme es que la aceleración tangencial sea cero.
\mbox{Movimiento uniforme}\qquad\qquad \Leftrightarrow \qquad\qquad \vec{a}_t=\vec{0}\quad\forall t
Un movimiento en el que la componente tangencial de la aceleración permanece constante en el tiempo (esto es, su rapidez varía uniformemente) se denomina uniformemente acelerado.
\mbox{Movimiento uniformemente acelerado}\qquad\qquad \Leftrightarrow \qquad\qquad a_t=\mathrm{cte}\quad\forall t
Aceleración normal
Mide el cambio en la dirección del movimiento (el giro del vector tangente). La condición para que un movimiento sea rectilíneo es que la aceleración normal sea nula en todo instante
\mbox{Movimiento rectilineo}\qquad\qquad \Leftrightarrow \qquad\qquad \vec{a}_n=\vec{0}\quad\forall t

8.4 Radio de curvatura

La aceleración normal puede escribirse en la forma

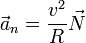
\vec{a}_n = \frac{v^2}{R}\vec{N}

donde R(t) es el llamado radio de curvatura de la trayectoria en ese instante. Este radio de curvatura es el radio de la llamada circunferencia osculatriz que es la que describiría una partícula que se moviera circularmente y tal que en ese instante ocupara la misma posición, tuviera la misma velocidad y la misma aceleración que la partícula real. El centro de esta circunferencia (centro de curvatura) está en cada instante en

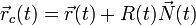
\vec{r}_c(t) = \vec{r}(t)+R(t)\vec{N}(t)

La curva formada por los sucesivos centros de curvatura se denomina evoluta de la trayectoria.

Un movimiento circular es entonces aquel que tiene radio y centro de curvatura constantes.

A partir de la expresión vectorial de la aceleración normal podemos obtener el radio de curvatura como

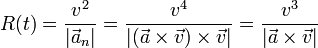
R(t) = \frac{v^2}{|\vec{a}_n|}= \frac{v^4}{|(\vec{a}\times\vec{v})\times\vec{v}|}=\frac{v^3}{|\vec{a}\times\vec{v}|}

A pesar de que esta expresión se calcula empleando la velocidad y la aceleración, que son específicas para cada movimiento concreto, el radio de curvatura y el centro de curvatura son propiedades puramente geométricas, independientes de la rapidez.

La inversa del radio de curvatura es la curvatura de la trayectoria

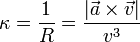
\kappa=\frac{1}{R}=\frac{|\vec{a}\times\vec{v}|}{v^3}

La curvatura, como el radio de curvatura, mide cuánto se dobla la trayectoria. Una curva muy cerrada posee un radio de curvatura pequeño y una curvatura grande. Una curva suave posee radio de curvatura grande y curvatura reducida. En particular una trayectoria rectilínea (que tiene aceleración normal nula) posee una curvatura igual a cero (y un radio de curvatura infinito).

8.5 Triedro de Frenet

Cuando se describe la dinámica de una partícula aparecen vectores, como una fuerza que actúe sobre la partícula, que no tienen por qué apuntar en la dirección de la velocidad o la aceleración. Para operar con estos vectores es conveniente expresar sus componentes en una determinada base vectorial.

Una posible base vectorial la constituye la base cartesiana \{\vec{\imath},\vec{\jmath},\vec{k}\}. Sin embargo, a menudo estamos interesados en aspectos geométricos concretos relacionados con el movimiento de la partícula. ¿Es la fuerza en la dirección de la velocidad? ¿Es perpendicular a ella? ¿Es perpendicular a la aceleración? Por ello, interesa definir una base vectorial relacionada con este movimiento. Interesa también que esta base sea ortonormal, por la simplicidad del cálculo en estas bases.

la base más adecuada la constituye el triedro de Frenet formado por tres vectores unitarios y perpendiculares entre sí, dos de los cuales ya conocemos:

Vector tangente
es el unitario tangente a la trayectoria, que se puede obtener normalizando la velocidad
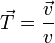
\vec{T}=\frac{\vec{v}}{v}
También puede calcularse considerando la derivada de la posición respecto a cualquier parámetro, no necesariamente el tiempo
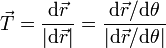
\vec{T}=\frac{\mathrm{d}\vec{r}}{|\mathrm{d}\vec{r}|}=\frac{\mathrm{d}\vec{r}/\mathrm{d}\theta}{|\mathrm{d}\vec{r}/\mathrm{d}\theta|}
En particular, si se emplea como variable el parámetro natural
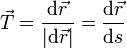
\vec{T}=\frac{\mathrm{d}\vec{r}}{|\mathrm{d}\vec{r}|}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}s}
Vector normal
es el unitario en la dirección de la aceleración normal
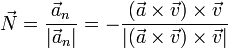
\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|} = -\frac{(\vec{a}\times\vec{v})\times\vec{v}}{|(\vec{a}\times\vec{v})\times\vec{v}|}
También puede hallarse normalizando la derivada del vector tangente respecto al tiempo o cualquier otra variable
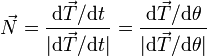
\vec{N}=\frac{\mathrm{d}\vec{T}/\mathrm{d}t}{|\mathrm{d}\vec{T}/\mathrm{d}t|} =\frac{\mathrm{d}\vec{T}/\mathrm{d}\theta}{|\mathrm{d}\vec{T}/\mathrm{d}\theta|}
Vector binormal
Para completar la base ortonormal podemos obtener un tercer vector multiplicando vectorialmente los dos anteriores
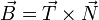
\vec{B}=\vec{T}\times\vec{N}
Alternativamente, el vector binormal puede hallarse directamente a partir de la velocidad y la aceleración
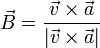
\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}
El vector binormal apunta en la dirección perpendicular al plano definido por la velocidad y la aceleración.

Alternativamente, dado que el vector binormal es más fácil de calcular a partir de la velocidad y la aceleración que el vector normal, es preferible hallar primero \vec{B} y luego \vec{N} como

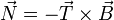
\vec{N} = -\vec{T}\times\vec{B}

Cualquier vector ligado a la partícula podrá escribirse entonces como la combinación lineal

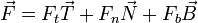
\vec{F}=F_t\vec{T}+F_n\vec{N}+F_b\vec{B}

Hay que destacar que el triedro de Frenet es dependiente de la posición. El vector tangente en un punto de la trayectoria será diferente del vector tangente en otro punto, y por tanto las componentes de los vectores irán cambiando de un punto a punto, aunque el vector no cambie.

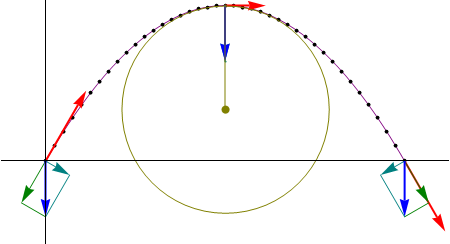
Componentes intrínsecas en el tiro parabólico

Por ejemplo, consideremos un tiro parabólico, en el cual el vector tangente, que siempre apunta en la dirección del movimiento irá cambiando. Lo mismo ocurre con el vector normal. Consideremos ahora la aceleración de este movimiento. Es un vector constante, pues 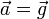\vec{a}=\vec{g} para un tiro parabólico. Sin embargo, la componente tangencial de la aceleración y la componente normal van cambiando, aunque la aceleración sea constante.

Los vectores de la base definen tres ejes coordenados (prolongando en la dirección de cada vector) y tres planos coordenados (combinando linealmente dos de ellos). Entre estos destaca

Recta tangente
Si en un instante dado t0 la partícula ocupa la posición 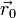\vec{r}_0 y se mueve con velocidad \vec{v}_0 la recta tangente a la trayectoria se obtiene prolongando hacia adelante y hacia atrás en la dirección de \vec{T} (o de la velocidad, que apunta en la misma dirección)
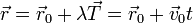
\vec{r}=\vec{r}_0 + \lambda\vec{T}=\vec{r}_0+\vec{v}_0t
Esta es la recta que seguiría una partícula que se moviera uniformemente y que pasar por el mismo punto y a la misma velocidad que la partícula real.
Plano osculador
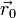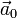Es el definido por los vectores tangente y normal. Si en un instante dado la partícula se encuentra en la posición \vec{r}_0, tiene velocidad \vec{v}_0 y aceleración \vec{a}_0, el plano osculador tiene la ecuación
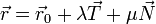
\vec{r}=\vec{r}_0 + \lambda\vec{T}+\mu\vec{N}
o, en términos de la velocidad y la aceleración
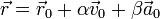
\vec{r}=\vec{r}_0 + \alpha\vec{v}_0+\beta\vec{a}_0
La ecuación vectorial de este plano es
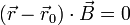
(\vec{r}-\vec{r}_0)\cdot\vec{B}=0
Una trayectoria es plana cuando se encuentra contenida siempre en el mismo plano, que será necesariamente el plano osculador (que está definido por la velocidad y la aceleración). Por ello, la condición matemática de curva plana es que
\mbox{Movimiento plano}\qquad\qquad\Leftrightarrow\qquad\qquad\vec{B}=\mathrm{cte.}

9 Ejemplos de movimientos

9.1 Rectilíneo

Un movimiento rectilíneo, como su nombre indica, es aquel cuya trayectoria es una recta. Cinemáticamente, esto se caracteriza porque su aceleración normal, responsable del cambio de dirección en la velocidad, es siempre nula. La velocidad y la aceleración son siempre paralelas en un movimiento rectilíneo

\mbox{Movimiento rectilineo}\qquad \Leftrightarrow \qquad\vec{T}=\mathrm{cte}\qquad \Leftrightarrow \qquad \vec{a}_n=\vec{0}\qquad \Leftrightarrow \qquad \vec{v}\times\vec{a}=\vec{0}\quad\forall t

En el caso de un movimiento rectilíneo, el paramétro arco no es más que la distancia medida sobre la recta en que se desplaza la partícula, de forma que la posición, velocidad y aceleración en cualquier instante se pueden escribir como

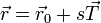
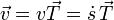
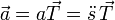
\vec{r}=\vec{r}_0 + s\vec{T}        \vec{v}=v\vec{T}=\dot{s}\,\vec{T}        \vec{a}=a\vec{T}=\ddot{s}\,\vec{T}

Puesto que la elección de ejes de coordenadas es arbitraria, si estamos estudiando el movimiento rectilíneo de una sola partícula, podemos tomar el eje X como la recta soporte del movimiento y reducir la descripción a una escalar

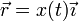
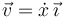
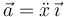
\vec{r}=x(t)\vec{\imath}        \vec{v}=\dot{x}\,\vec{\imath}        \vec{a}=\ddot{x}\,\vec{\imath}

9.1.1 Rectilíneo uniformemente acelerado

Un caso particular de movimiento rectilíneo es aquel en que la aceleración es una constante

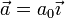
\vec{a}=a_0\vec{\imath}

En este movimiento la celeridad aumenta linealmente con el tiempo

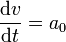
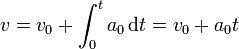
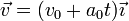
\frac{\mathrm{d}v}{\mathrm{d}t}=a_0   \Rightarrow   v = v_0+\int_0^ta_0\,\mathrm{d}t=v_0+a_0t   \Rightarrow   \vec{v}=(v_0+a_0t)\vec{\imath}

y la posición varía de forma cuadrática con el tiempo

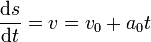
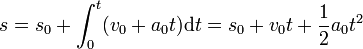
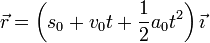
\frac{\mathrm{d}s}{\mathrm{d}t}=v=v_0+a_0t   \Rightarrow   s=s_0+\int_0^t(v_0+a_0t)\mathrm{d}t=s_0+v_0t+\frac{1}{2}a_0t^2   \Rightarrow   \vec{r}=\left(s_0+v_0t+\frac{1}{2}a_0t^2\right)\vec{\imath}

9.1.2 Rectilíneo y uniforme

Otro caso particular de movimiento es el que tiene aceleración nula. En este caso

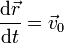
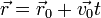
\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\vec{v}_0   \Rightarrow   \vec{r}=\vec{r}_0+\vec{v_0}t

En el caso de una velocidad constante, el movimiento resultante es siempre rectilíneo y uniforme.

9.2 Parabólico

Artículo completo: Cinemática del tiro parabólico

El movimiento parabólico, característico del tiro de un proyectil, se caracteriza por tener una aceleración constante debida a la gravedad

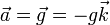
\vec{a}=\vec{g}=-g\vec{k}

(tomando como eje Z el perpendicular al suelo y dirigido hacia arriba). Integrando esta ecuación una vez obtenemos la velocidad instantánea

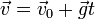
\vec{v} = \vec{v}_0 + \vec{g}t

y una nueva integración nos da la posición instantánea:

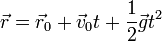
\vec{r}=\vec{r}_0 + \vec{v}_0t+\frac{1}{2}\vec{g}t^2

Este movimiento es plano, ya que su vector binormal es constante

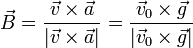
\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}=\frac{\vec{v}_0\times\vec{g}}{|\vec{v}_0\times\vec{g}|}

Si tomamos el eje X como el que pertenece al plano de movimiento podemos escribir la posición instantánea como

\vec{r}=(x_0+v_{x0}t)\vec{\imath}+\left(z_0+v_{z0}t-\frac{1}{2}gt^2\right)\vec{k}

Esta ecuación puede leerse como que el movimiento parabólico es una superposición de un movimiento uniforme en la dirección horizontal y uno uniformemente acelerado en la dirección vertical.

Eliminando el tiempo entre las dos coordenadas obtenemos una ecuación para la trayectoria

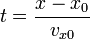
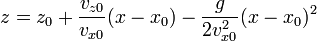
t = \frac{x-x_0}{v_{x0}}   \Rightarrow    z = z_0 + \frac{v_{z0}}{v_{x0}}(x-x_0) -\frac{g}{2v_{x0}^2}(x-x_0)^2

Al tratarse de un polinomio de segundo grado, es claro que la trayectoria es una parábola dirigida hacia abajo.

Aunque la aceleración sea constante, tanto la aceleración tangencial como la normal son funciones del tiempo. La celeridad de la partícula disminuye al ascender y vuelve a aumentar al descender, alcanzando su mínimo en el vértice de la parábola. En este punto, la aceleración tangencial es nula y toda la aceleración es puramente normal.

9.3 Circular

Un movimiento circular es aquel cuya trayectoria es una circunferencia. Esto implica que

  • El movimiento es plano: Existe un vector constante \vec{B} tal que
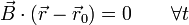
\vec{B}\cdot(\vec{r}-\vec{r}_0)=0\qquad\forall t
  • El radio de curvatura permanece constante:
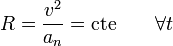
R = \frac{v^2}{a_n}=\mathrm{cte}\qquad\forall t

Estas dos condiciones pueden reducirse a una sola:

  • El centro de curvatura permanece constante:
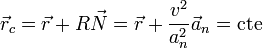
\vec{r}_c = \vec{r}+R\vec{N}=\vec{r}+\frac{v^2}{a_n^2}\vec{a}_n=\mathrm{cte}

Por tanto, dadas la ecuación horaria del movimiento o, más en general, la trayectoria en función de cualquier parámetro, si calculamos el centro de curvatura y resulta un vector constante el movimiento es circular, aunque en la expresión no sea evidente.

9.3.1 Velocidad angular

En cualquier movimiento, se verifica en todo instante que

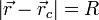
\left|\vec{r}-\vec{r}_c\right| = R

en el caso particular de un movimiento circular R y \vec{r}_c son constantes, por lo que si elevamos al cuadrado esta expresión

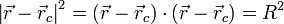
\left|\vec{r}-\vec{r}_c\right|^2 = (\vec{r}-\vec{r}_c)\cdot(\vec{r}-\vec{r}_c)=R^2

y derivamos respecto al tiempo

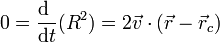
0 = \frac{\mathrm{d}\ }{\mathrm{d}t}(R^2) = 2\vec{v}\cdot(\vec{r}-\vec{r}_c)

esto es, la velocidad es siempre perpendicular al vector de posición relativa al centro de la circunferencia. Esta ortogonalidad permite escribir la velocidad como

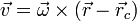
\vec{v} = \vec{\omega}\times\left(\vec{r}-\vec{r}_c\right)

donde \vec{\omega} es la velocidad angular. Es un vector perpendicular al plano de la trayectoria circular y con un sentido tal que se verifica la regla de la mano derecha respecto al giro (si los dedos de la mano derecha apuntan en la dirección del giro, el pulgar marca la dirección y sentido de la velocidad angular).

La velocidad angular posee dimensiones de 1/tiempo, con lo que en el sistema internacional se mide en s-1 o rad/s.

9.3.2 Aceleración angular

Derivando en la expresión anterior para la velocidad

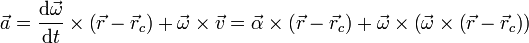
\vec{a}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}\times\left(\vec{r}-\vec{r}_c\right)+\vec{\omega}\times\vec{v}=\vec{\alpha}\times\left(\vec{r}-\vec{r}_c\right)+\vec{\omega}\times\left(\vec{\omega}\times\left(\vec{r}-\vec{r}_c\right)\right)

El vector

\vec{\alpha} = \frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}

es la aceleración angular del movimiento. En el sistema internacional, sus unidades son rad/s².

9.3.3 Movimiento circular uniforme

El movimiento circular uniforme es el que ocurre a celeridad constante

v = v_0=\mathrm{cte}\qquad \Leftrightarrow \qquad \vec{a}_t=\vec{0}

En este movimiento la velocidad no es constante, puesto que su dirección está cambiado. La aceleración es puramente normal

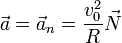
\vec{a}=\vec{a}_n = \frac{v_0^2}{R}\vec{N}

lo que implica que la aceleración va en la dirección de la posición relativa al centro de la circunferencia, y dirigida hacia adentro y puesto que estos dos vectores son de módulo constante se cumple

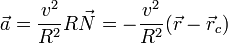
\vec{a} = \frac{v^2}{R^2}R\vec{N}=-\frac{v^2}{R^2}(\vec{r}-\vec{r}_c)

En un movimiento circular uniforme la velocidad angular es constante

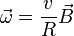
\vec{\omega}=\frac{v}{R}\vec{B}

y la aceleración angular es nula

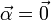
\vec{\alpha}=\vec{0}

La aceleración puede escribirse en términos de la velocidad angular como

\vec{a}=\vec{\omega}\times(\vec{\omega}\times(\vec{r}-\vec{r}_c))=-\omega^2(\vec{r}-\vec{r}_c)

Un movimiento circular uniforme es periódico, siendo el periodo de revolución el tiempo necesario para dar una vuelta completa

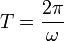
T = \frac{2\pi}{\omega}

Al número de vueltas que la partícula da por segundo se le denomina la frecuencia natural

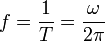
f = \frac{1}{T}=\frac{\omega}{2\pi}

9.3.4 Movimiento en el plano XY

Puesto que los sistemas de referencia son arbitrarios, una vez que sabemos que un movimiento es circular, podemos tomar el origen de coordenadas en el centro de la circunferencia y los ejes de forma que la trayectoria esté contenida en el plano XY. En este caso la ecuación de la trayectoria se reduce a

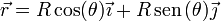
\vec{r}=R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}\,(\theta)\vec{\jmath}

siendo la ley horaria

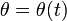
\theta = \theta(t)\,

La velocidad de un movimiento circular expresado de esta forma es

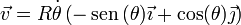
\vec{v}=R\dot{\theta}\left(-\,\mathrm{sen}\,(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right)

siendo la celeridad y el vector tangente

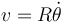
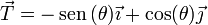
v = R\dot{\theta}        \vec{T}=-\,\mathrm{sen}\,(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}

El parámetro arco vale

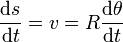
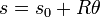
\frac{\mathrm{d}s}{\mathrm{d}t}=v = R\frac{\mathrm{d}\theta}{\mathrm{d}t}   \Rightarrow    s = s_0+R\theta\,

La velocidad angular va en la dirección normal al plano y es tal que al multiplicarla vectorialmente por \vec{r} resulta la velocidad. Esto da

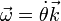
\vec{\omega}=\dot{\theta}\vec{k}

La aceleración de la partícula es

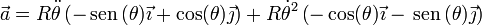
\vec{a}=R\ddot{\theta}\left(-\,\mathrm{sen}\,(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right)+R\dot{\theta}^2\left(-\cos(\theta)\vec{\imath}-\,\mathrm{sen}\,(\theta)\vec{\jmath}\right)

con componentes intrínsecas

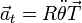
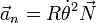
\vec{a}_t = R\ddot{\theta}\vec{T}        \vec{a}_n=R\dot{\theta}^2\vec{N}

con el vector normal

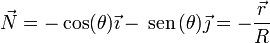
\vec{N}=-\cos(\theta)\vec{\imath}-\,\mathrm{sen}\,(\theta)\vec{\jmath}=-\frac{\vec{r}}{R}

Por último, la aceleración angular viene dada por

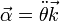
\vec{\alpha}=\ddot{\theta}\vec{k}

Con estos ejes, un movimiento circular uniforme corresponde a

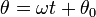
\theta = \omega t + \theta_0\,

con ω constante.

9.4 Helicoidal

Una hélice es una curva tridimensional en la cual se produce un movimiento de giro en torno a un eje simultáneamente a un avance en la dirección paralela a dicho eje. Si tomamos el eje de la hélice como eje Z, las ecuaciones paramétricas de la hélice son

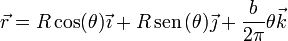
\vec{r}=R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}\,(\theta)\vec{\jmath}+\frac{b}{2\pi}\theta\vec{k}

Cuando la partícula efectúa una revolución completa en torno al eje Z (el parámetro θ varía en 2π), al mismo tiempo avanza una cantidad b en la dirección del eje Z. Este b es el denominado paso de rosca de la hélice. Empleando distancias tenemos que mientras describe una circunferencia de longitud 2πR asciende una cantidad b, con lo cual la inclinación de la hélice es

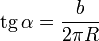
\mathrm{tg}\,\alpha = \frac{b}{2\pi R}

Un movimiento helicoidal es entonces uno que recorre una porción de hélice en el tiempo (no necesariamente de manera uniforme).

La velocidad de una partícula en un movimiento helicoidal se obtiene derivando respecto al tiempo (no respecto a θ, esta variable también debe ser derivada)

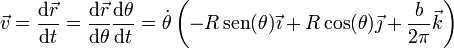
\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\frac{\mathrm{d}\theta}{\mathrm{d}t} = \dot{\theta}\left(-R\,\mathrm{sen}(\theta)\vec{\imath}+R\cos(\theta)\vec{\jmath}+\frac{b}{2\pi}\vec{k}\right)

La velocidad en un movimiento helicoidal puede expresarse como la suma de una componente paralela al eje (deslizamiento) y otra componente perpendicular a él de tipo circular

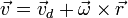
\vec{v} = \vec{v}_d + \vec{\omega}\times\vec{r}

donde

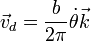
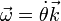
\vec{v}_d = \frac{b}{2\pi}\dot{\theta}\vec{k}        \vec{\omega}=\dot{\theta}\vec{k}

Vemos que la velocidad de deslizamiento es paralela a la velocidad angular y existe una proporcionalidad constante entre ambas

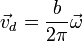
\vec{v}_d = \frac{b}{2\pi}\vec{\omega}

Equivalentemente, si lo que conocemos son la velocidad angular y de deslizamiento de un movimiento helicoidal, podemos determinar su paso de rosca a partir del cociente entre sus módulos.

La celeridad en un movimiento helicoidal vale

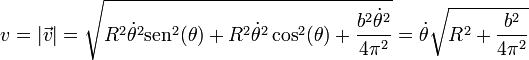
v = |\vec{v}| = \sqrt{R^2\dot{\theta}^2\mathrm{sen}^2(\theta)+R^2\dot{\theta}^2\cos^2(\theta)+\frac{b^2\dot{\theta}^2}{4\pi^2}} = \dot{\theta}\sqrt{R^2+\frac{b^2}{4\pi^2}}

Dado que existe una proporcionalidad entre la celeridad y la derivada temporal del parámetro θ, podemos obtener de forma inmediata la parametrización natural de la hélice

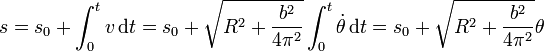
s = s_0 + \int_0^t v\,\mathrm{d}t = s_0 + \sqrt{R^2+\frac{b^2}{4\pi^2}}\int_0^t \dot{\theta}\,\mathrm{d}t = s_0+\sqrt{R^2+\frac{b^2}{4\pi^2}}\theta

Se puede comprobar que el radio de curvatura de un movimiento helicoidal es constante (pero no coincide con el radio R de la hélice).

9.5 Armónico simple

El movimiento armónico simple (M.A.S.) es un caso particular de movimiento rectilíneo (que, por tanto, se puede describir mediante cantidades escalares), caracterizado por la ecuación de movimiento

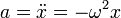
a = \ddot{x} = -\omega^2 x

siendo ω una constante.

La expresión general de un posible desplazamiento que verifique esta ecuación es

x = A\cos(\omega t + \beta)\,

siendo A y β dos constantes que se pueden calcular a partir de la posición y la velocidad inicial.

El movimiento armónico simple también se puede definir de forma alternativa como el obtenido al proyectar un movimiento circular uniforme sobre un diámetro cualquiera de la circunferencia.

La velocidad y la aceleración instantáneas se calculan derivando la expresión de x(t):

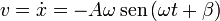
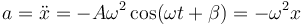
v = \dot{x} = -A\omega\,\mathrm{sen}\,(\omega t+\beta)    a = \ddot{x}=-A\omega^2\cos(\omega t + \beta)=-\omega^2 x\,

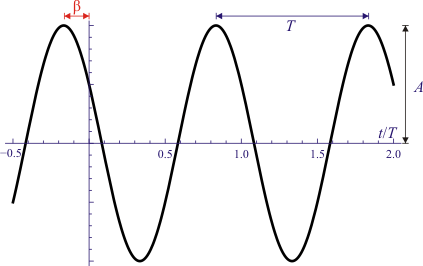
Si representamos la posición a lo largo del eje X como función del tiempo obtenemos una función periódica

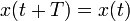
x(t+T) = x(t)\,

con T el periodo de oscilación. La forma de la función es sinusoidal. Este movimiento se caracteriza por los siguientes variables y constantes:

Elongación, x(t)
es la posición instantánea, considerada como distancia (con signo) respecto a la posición central del movimiento.
Fase, φ = ωt + β
Indica en que punto del ciclo se encuentra el sistema. Para un periodo varía entre 0 y 2π rad.
Amplitud, A
es la máxima elongación del movimiento. Se mide en m en el SI.
Frecuencia angular, ω
En el SI se mide en rad/s.
Periodo, T
Es el intervalo necesario para una oscilación completa. Se calcula a partir de la frecuencia angular como
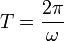
T = \frac{2\pi}{\omega}
En el SI el periodo se mide en s.
Frecuencia natural, f
mide el número de oscilaciones que el sistema realiza en la unidad de tiempo. Es la inversa del periodo
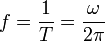
f=\frac{1}{T}=\frac{\omega}{2\pi}
En el SI se mide en hercios, Hz, equivalentes a 1 ciclo/s o simplemente a 1 s−1.
Constante de fase, β
También llamada fase inicial. Es proporcional al adelanto (fracción de período transcurrida) entre el instante de máxima elongación (que corresponde a una fase φ = 0) y el instante inicial (t=0).

La velocidad y la aceleración de este movimiento son también funciones oscilatorias, con el mismo periodo pero desfasadas, un cuarto de periodo la velocidad y medio periodo la aceleración. En un periodo de oscilación, cuando la elongación es máxima, la velocidad es nula y la aceleración es máxima (pero de signo contrario a la elongación). En el punto central la elongación y la aceleración son nulas, mientras que la velocidad es máxima.

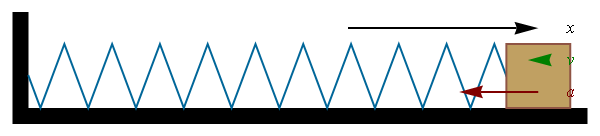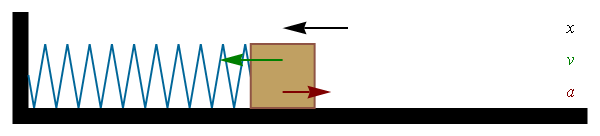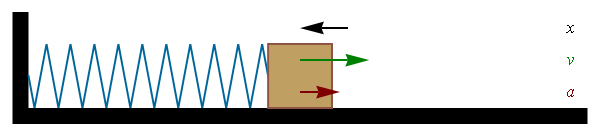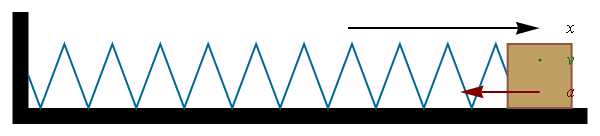
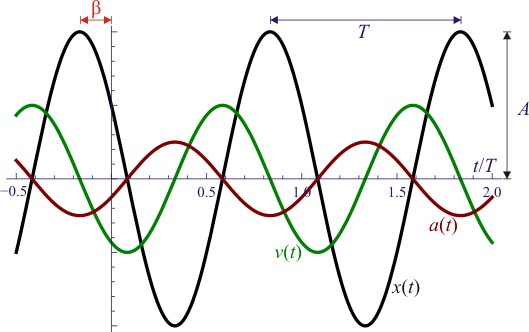
Archivo:muelle.gif    Archivo:oscilaciones-mas.png

El movimiento armónico simple es característico de los osciladores armónicos, que son sistemas sometidos a una fuerza recuperadora lineal (según la ley de Hooke). Por ello, será estudiado más extensamente en el tema de movimiento oscilatorio.

10 Problemas

Obtenido de "http://tesla.us.es/wiki/index.php/Cinem%C3%A1tica_de_la_part%C3%ADcula_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace