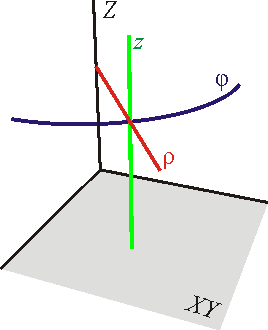
Coordenadas cilíndricas. Líneas y superficies coordenadas

De Laplace

1 Líneas coordenadas

• La coordenada vertical, , es la misma que en cartesianas, y lo mismo ocurre con su línea coordenada, que será una recta vertical que pasa por .
• Para la coordenada radial 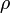, al mover esta coordenada nos acercamos o alejamos del eje 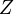sin variar la altitud ni la dirección. Las líneas serán entonces semirrectas horizontales que parten del eje 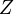y pasan por . Son semirrectas y no rectas, porque No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \rho\ge 0\,<\math> siempre. * Al variar la coordenada <math>\varphi

cambiamos el ángulo con el eje , sin modificar ni la distancia al eje ni la altura. Por tanto, las líneas coordenadas   son circunferencias horizontales.

2 Superficies coordenadas

3 Artículo siguiente

Coordenadas esféricas. Líneas y superficies coordenadas

4 Artículo siguiente

Coordenadas cartesianas. Líneas y superficies coordenadas

5 Artículos relacionados

Coordenadas cilíndricas. Definición