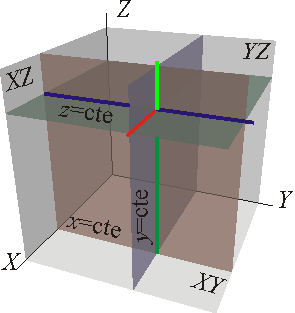
Coordenadas cartesianas. Líneas y superficies coordenadas
De Laplace
Revisión a fecha de 20:20 19 nov 2007; Gonfer (Discusión | contribuciones)
Contenido |
1 Líneas coordenadas
variamos 
, manteniendo fijos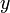 
y 
, lo que hacemos es seguir una línea recta, paralela al eje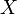 
. Análogamente ocurre si variamos 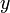o si variamos . Como cada coordenada se extiende desde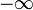 
a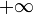 
, estas rectas se entienden indefinidamente en los dos sentidos. Por tanto, las líneas coordenadas en cartesianas que pasan por un punto son tres rectas ortogonales entre sí y paralelas a los ejes de coordenadas.
2 Superficies coordenadas
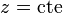es un plano horizontal.
el mismo modo, las superficies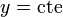 
y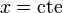 
son planos verticales, ortogonales entre sí.
Las superficies coordenadas cartesianas en cada punto P, por tanto, son planos ortogonales dos a dos, y paralelos a los planos coordenados.
3 Artículo siguiente
Coordenadas cilíndricas. Líneas y superficies coordenadas
4 Artículo anterior
Líneas y superficies coordenadas
