Problemas de introducción a la dinámica

De Laplace

1 Partícula que impacta con un muelle

Una masa m se encuentra al borde de una pendiente. Después de la pendiente se extiende una llanura, al final de la cual hay un muelle relajado de constante elástica k y longitud natural l₀. La masa se encuentra a una altura h relativa al muelle. Suponemos que no existe fuerza de rozamiento entre la masa y la superficie.

1. Determine la velocidad con la que la masa impacta en el muelle (punto B).
2. ¿Cuál es el valor mínimo de la constante elástica del muelle, k_min, para que este pueda evitar que la masa toque la pared?
3. Suponga ahora que entre los puntos A y B hay una región de longitud d en la que existe rozamiento entre la masa y el suelo. Si el coeficiente de rozamiento es μ, ¿cuál es el nuevo valor mínimo de k en el apartado anterior?
4. Supongamos que k > k_min. En la situación de rozamiento del apartado anterior, calcule la velocidad con la que la partícula vuelve al punto A y la altura a la que sube por la pendiente.
5. Calcule numéricamente las magnitudes pedidas si 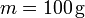, , 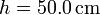, 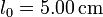μ = 0.200, , .

Solución

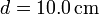2 Partícula que desliza sobre un disco

Una partícula P, de masa m, es abandonada en reposo en el punto más alto de un disco vertical de radio R que descansa apoyado en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determina el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo.

Solución

3 Partícula en un tubo con muelle

Un tubo delgado, hueco y de masa despreciable, está situado en el plano horizontal OXY pudiendo rotar libremente y sin rozamiento alrededor del eje fijo (eje OZ) que pasa por su punto medio (punto O). En el interior del tubo se halla una partícula P, de masa m, que es atraída hacia el punto O con una fuerza directamente proporcional a la distancia entre P y O (con constante de proporcionalidad k) Suponiendo que todos los contactos son lisos, y utilizando las coordenadas polares ρ y θ, así como sus derivadas temporales de primer y segundo orden, se pide:

1. Escribir las ecuaciones dinámicas de la partíıcula (Segunda Ley de Newton proyectada en las direcciones radial y acimutal) en el sistema inercial OXY y en el sistema no inercial solidario con el tubo.
2. Se hace rotar el tubo con velocidad angular constante ω₀. Determina qué inecuación debe verificar ω₀ respecto a m y k para que el movimiento de la partícula respecto al tubo pueda ser armónico simple.

Solución