Problemas de dinámica de un sistema de partículas

De Laplace

1 Cuatro partículas en un cuadrado

Se tienen 4 masas que ocupan los vértices de un cuadrado de lado 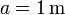. Calcula la posición del centro de masas del sistema en cada uno de los casos siguientes

1. .
2. , .
3. , .
4. , .

Solución

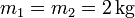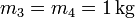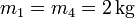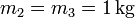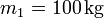2 Centro de masas de sistemas continuos

Calcula por integración la posición del centro de masas de estos dos sistemas

1. Una barra homogénea delgada de longitud h y masa M.
2. Una barra homogénea delgada en forma de semicírculo de radio a y masa M.

Solución

3 Dos partículas unidas por un oscilador armónico

Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad v₀ alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?

Solución

4 Ejemplo de un sistema de partículas

Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son, en el SI,

i	mi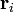
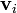
1	5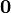
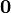
2	4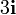
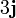
3	3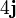

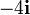
Las tres partículas están conectadas por resortes con la misma constante k = 30N / m y longitud natural nula. No hay más fuerzas actuando en el sistema. Para el instante indicado:

1. Determina la aceleración de cada partícula.
2. Calcula la posición, velocidad y aceleración del CM.
3. Calcula el momento cinético del sistema respecto al origen y respecto al CM.
4. Halla la energía cinética del sistema respecto al origen y respecto al CM.
5. Calcula las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.

Solución

5 Momento cinético de una barra

Una barra homogénea de masa m y longitud L gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular uniforme .

1. Calcula el momento angular de la barra respecto a su punto central.
2. Ahora el eje de giro pasa por uno de sus extremos. Calcula el momento angular de la barra en este caso, respecto a un punto del eje de giro.
3. En la situación anterior, la longitud de la barra se multiplica por dos, mientras que su masa permanece constante. ¿Cómo cambia la velocidad angular? ¿Y si se divide por dos?

Solución

6 Dos partículas unidas por una barra

Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v₀ perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?

Solución

7 Propulsión a reacción

Un cohete a reacción se impulsa en el espacio emitiendo gases a cierta velocidad en el sentido opuesto a su propio movimiento. Sea un cohete que tiene una masa M₀ y lleva una carga inicial de combustible m₀. Este combustible es expulsado a ritmo constante 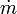con una velocidad constante respecto a la nave, v₀. Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?

Solución

8 Colisiones de dos partículas

Una partícula de masa M se encuentra en reposo. Otra partícula de masa mimpacta con ella con una velocidad v. Después del choque las dos partículas se mueven en la misma dirección en la que se movía la partÍcula m.

1. Encuentra la expresión de la velocidad de cada una de las partículas en función de sus masas y de v si el choque es perfectamente elástico.
2. Calcula la velocidad si el choque es completamente inelástico. ¿Cuánta energía cinética se pierde en el choque?
3. ¿Qué ocurre si 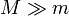? ¿Y si ?

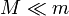Solución