Materiales magnéticos
De Laplace
Contenido |
1 Introducción
Este tema constituye el segundo del bloque de Magnetostática. En el se estudian brevemente las propiedades de los campos magnéticos en presencia de medios materiales, las ecuaciones que describen dichos campos y los tipos de materiales, atendiendo a sus propiedades magnéticas.
El esquema que se sigue en este tema sigue una estrecha analogía con el tema de Campo eléctrico en presencia de dieléctricos.
2 Magnetización
2.1 Definición
El campo magnético se ve afectado por la presencia de medios materiales, porque estos están constituidos por dipolos magnéticos, tanto orbitales como intrínsecos (el espín). Para describir esta distribución de dipolos en forma macroscópica se define la magnetización o imanación de un material en un punto como la densidad
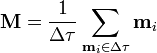
siendo Δτ un pequeño elemento de volumen en torno al punto 
.
2.2 Potencial vector de una magnetización
El potencial vector debido a una magnetización es una extensión de la expresión correspondiente a un solo dipolo
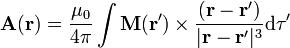
3 Corrientes de magnetización
La expresión del potencial vector puede transformarse en suma de potenciales vectores debidos a densidades de corriente
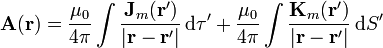
donde
![\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]](/wiki/images/math/f/7/e/f7e32e5788be56963bc508bf82ea6658.png)
son las llamadas densidades de corriente de magnetización, de volumen y de superficie, respectivamente.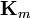 
existe en las interfaces entre dos materiales. En el caso particular de la frontera entre un medio magnetizado y el exterior, esta densidad se reduce a 
.
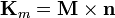4 Ecuaciones de la magnetostática en medios materiales
Empleando las densidades de corriente de magnetización las ecuaciones para el campo magnético quedan como
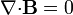
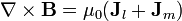
y las condiciones de salto en las interfaces
![\mathbf{n}{\cdot}[\mathbf{B}]=0](/wiki/images/math/a/7/c/a7c1b1fa7de15ce1ab4d527595188456.png)
![\mathbf{n}\times[\mathbf{B}]=\mu_0(\mathbf{K}_l+\mathbf{K}_m)](/wiki/images/math/f/e/c/fec80b926ee0f47511e075c507113255.png)
siendo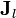 
y 
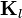las {densidades de corriente libres, definidos como aquellas que no son de magnetización.
5 Campo magnético H
A menudo las densidades de corriente de magnetización son cantidades desconocidas a priori, por lo que interesa eliminarlas de las
ecuaciones. Esto se consigue definiendo un campo auxiliar denominado campo magnético 
(para evitar confusiones con 
, conviene acompañar el nombre por el vector que lo representa). El campo se define como
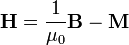
o, equivalentemente,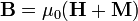 
. En términos de y las ecuaciones de la magnetostática se expresan
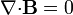
y las condiciones de salto
![\mathbf{n}\times[\mathbf{H}]=\mathbf{K}_l](/wiki/images/math/b/0/a/b0a623e3927c5122a33804a7dfe14331.png)
Estas ecuaciones no son completas, ya que deben suplementarse con una relación constitutiva que relacione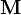 
con (o, como se expresa habitualmente 
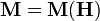o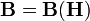 
).
Las ecuaciones de la magnetostática pueden escribirse en términos del campo exclusivamente. Sustituyendo la definición de en las ecuaciones para las fuentes escalares resulta
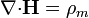
con condiciones de salto
![\mathbf{n}{\cdot}[\mathbf{H}]=\sigma_m](/wiki/images/math/8/3/5/83541e34ead8c95cb240f3334e9d186f.png)
donde ρm y σm son las llamadas densidades de carga magnética, definidas como
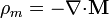
![\sigma_m =-\mathbf{n}{\cdot}[\mathbf{M}]](/wiki/images/math/7/f/3/7f3e512131c4d631ee839da4aeeba3cb.png)
Estas densidades de carga constituyen una descripción equivalente a la magnetización, alternativa a la de las corrientes de magnetización. Es en función de ρm y σm que se puede expresar el campo magnético en términos de polos norte (densidad de carga positiva) y sur (densidad negativa), y las fuerzas magnéticas a partir de la interacción entre ellos.
El campo posee tanto fuentes escalares como vectoriales. Sin embargo, en problemas de materiales con magnetización permanente (imanes) las densidades de corrientes libres pueden anularse y el campo hacerse irrotacional, lo que permite establecer un paralelismo con el campo electrostático, con las cargas magnéticas ocupando el lugar de las eléctricas.
6 Materiales magnéticos
Las relaciones constitutivas que caracterizan los distintos materiales presentan una gran diversidad, a diferencia de lo que ocurre con los dieléctricos o con los medios conductores.
Entre los distintos tipos de materiales, los más importantes son los siguientes:
6.1 Medios lineales
Son aquellos en los que la magnetización es proporcional al campo magnético
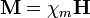
siendo \chi_m la susceptibilidad magnética. Para los medios lineales, el campo magnético es también proporcional al campo magnético
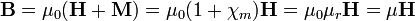
La cantidad μr = 1 + χm es la denominada permeabilidad relativa del medio, mientras que μ = μ0μr es la permeabilidad absoluta.
Dependiendo del signo de \chi_m, los materiales lineales se dividen en dos grupos: diamagnéticos y paramagnéticos.
6.1.1 Diamagnéticos
Poseen una susceptibilidad negativa. En estos materiales, el campo se ve reducido por efecto de la magnetización inducida, que se opone al campo externo. Para casi todos los diamagnéticos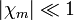 
y puede aproximarse 
.
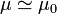6.1.2 Paramagnéticos
Tienen una susceptibilidad positiva. En los materiales paramagnéticos la magnetización refuerza al campo externo. La mayoría de los medios paramagnéticos tienen una susceptibilidad muy pequeña y 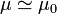. No obstante, existen sustancias paramagnéticas con muy alta susceptibilidad; estas sustancias, a bajas temperaturas se transforman en ferromagnéticas.
6.2 Ferromagnéticos
Se caracterizan por ser capaces de presentar una magnetización remanente en ausencia de campo externo, pudiendo ser empleados como imanes permanentes. Cuando se les aplica un campo externo presentan lo que se denomina ciclo de histéresis}. El estado, para un campo $H$ dado, depende del proceso previo. Cuando el campo aplicado es muy intenso, los materiales ferromagnéticos presentan saturación. Al reducir el campo a cero, persiste una magnetización remanente, Mr. Es necesario aplicar un campo opuesto (campo coercitivo, Hc) para reducir la imanación a cero. Con un campo opuesto más intenso, vuelve a aparecer la saturación y el proceso puede repetirse en sentido opuesto. Los ferromagnéticos se dividen en blandos, cuando Hc es pequeño, y duros, si Hc es grande.
Para campos débiles, si Mr es nulo, los ferromagnéticos se comportan aproximadamente como paramagnéticos de alta permeabilidad.
El ciclo de histéresis desaparece cuando la temperatura del material excede la llamada temperatura de Curie, a partir de la cual son paramagnéticos.
6.3 Ferritas
También conocidos como ferrimagnéticos. Similares a los ferromagnéticos en su comportamiento frente a un campo magnético, con la diferencia de que su conductividad eléctrica es muy inferior, lo que reduce las pérdidas por efecto Joule. Suelen ser óxidos metálicos como la magnetita.
