Entrar Página Discusión Historial Go to the site toolbox

Movimiento de un péndulo

De Laplace

Revisión a fecha de 21:52 24 ago 2015; Antonio (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado

Tenemos un péndulo simple formado por una lenteja de 0.5 kg que cuelga de una varilla rígida de masa despreciable y 1.20 m de longitud.

  1. Si se separa la lenteja de la vertical un ángulo de 5° y se suelta desde el reposo, ¿con qué rapidez pasa la masa por el punto más bajo? ¿Cuánto tiempo tarda en llegar a esta posición?
  2. ¿Cuánto vale la tensión de la varilla en el momento de soltar la masa? ¿Y en el punto más bajo?
  3. Suponga que se ajusta un reloj suponiendo que se usa el péndulo anterior, pero resulta que en realidad la varilla mide 115 cm. El reloj ¿atrasa o adelanta? ¿Cuánto cada día?

2 Introducción

El péndulo simple se analiza de forma general en el apartado teórico del tema de de dinámica y se vuelve a revisar en el de energía y leyes de conservación. Aquí solo veremos los resultados concretos para este caso.

3 Rapidez y periodo

Cuando la amplitud de las oscilaciones es pequeña, el péndulo sigue aproximadamente un movimiento armónico de ecuación

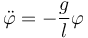
\ddot{\varphi}=-\frac{g}{l}\varphi

Si la partícula parte del reposo con un ángulo de separación 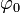\varphi_0, la solución para todo instante es

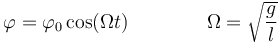
\varphi=\varphi_0\cos(\Omega t) \qquad\qquad\Omega = \sqrt{\frac{g}{l}}

La velocidad angular con la que se mueve la lenteja respecto al punto de anclaje es

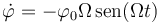
\dot{\varphi}=-\varphi_0\Omega\,\mathrm{sen}(\Omega t)

El punto más bajo corresponde a 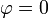\varphi=0 lo cual ocurre en un cierto instante t1 dado por

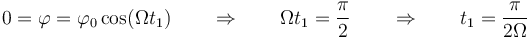
0=\varphi = \varphi_0\cos(\Omega t_1)\qquad \Rightarrow\qquad\Omega t_1 = \frac{\pi}{2} \qquad \Rightarrow\qquad t_1 = \frac{\pi}{2\Omega}

con el valor numérico

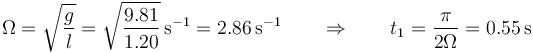
\Omega = \sqrt{\frac{g}{l}}=\sqrt{\frac{9.81}{1.20}}\,\mathrm{s}^{-1}=2.86\,\mathrm{s}^{-1}\qquad\Rightarrow\qquad t_1 = \frac{\pi}{2\Omega}=0.55\,\mathrm{s}

El periodo de oscilación será cuádruple de este tiempo, es decir, 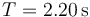T = 2.20\,\mathrm{s}

Para ese instante t1 el seno vale la unidad, por lo que

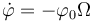
\dot{\varphi}=-\varphi_0\Omega

Larapidez de la partícula en ese instante es igual a

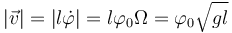
|\vec{v}|=|l\dot{\varphi}|=l\varphi_0\Omega = \varphi_0\sqrt{gl}

siendo su valor numérico

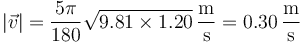
|\vec{v}|=\frac{5\pi}{180}\sqrt{9.81\times 1.20}\,\frac{\mathrm{m}}{\mathrm{s}} = 0.30\,\frac{\mathrm{m}}{\mathrm{s}}

4 Tensión del hilo

Cuando pasa por el punto más bajo, las dos fuerzas que actúan sobre la partícula (el peso y la tensión del hilo) son normales a la trayectoria, y por tanto toda la aceleración es normal, siendo el radio de curvatura igual a la longitud del hilo

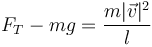
F_T-mg = \frac{m|\vec{v}|^2}{l}

de donde

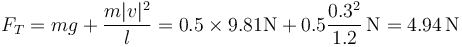
F_T = mg + \frac{m|v|^2}{l}= 0.5\times 9.81\mathrm{N}+0.5\frac{0.3^2}{1.2}\,\mathrm{N} = 4.94\,\mathrm{N}

Alternativamente, podemos sustituir aquí la rapidez del movimiento y queda

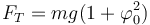
F_T = mg(1 + \varphi_0^2)\,

con valor numérico

F_T = mg\left(1+\left(\frac{5\pi}{180}\right)^2\right) = 1.0076mg = 1.0076\times 0.5\times 9.81\,\mathrm{N}= 4.94\,\mathrm{N}

Vemos que la tensión es mayor en un 0.7% a la que tendría estándo en reposo (4.90 N).

5 Comparación de dos péndulos

El periodo de un péndulo es igual a

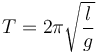
T = 2\pi\sqrt{\frac{l}{g}}

Por tanto, si tenemos dos péndulos de diferente longitud, la proporción entre sus periodos es

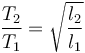
\frac{T_2}{T_1}=\sqrt{\frac{l_2}{l_1}}

si nos dicen que la longitud es de 115 cm en lugar de 120 cm, queda

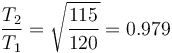
\frac{T_2}{T_1}=\sqrt{\frac{115}{120}}=0.979

Es decir, que el periodo del péndulo más corto es un 2% más breve que el del largo. Esto quiere decir que el reloj adelanta, para hacer las oscilaciones que el largo realiza en 24 horas, el corto emplea solo 23h30min, es decir, adelanta media hora por día.

Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_de_un_p%C3%A9ndulo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace