Péndulos e hilos (GIE)

De Laplace

Contenido

1 Tensión de un hilo
2 Péndulo simple
3 Máquina de Atwood

1 Tensión de un hilo

Uno de los elementos más comunes en problemas de dinámica es la presencia de hilos flexibles conectados a diferentes cuerpos, anclajes fijos o pasando por poleas. Estos hilos, en primera aproximaciones se consideran como ideales:

No tienen masa
Son inextensibles

Al ser inextensibles, garantizan que la distancia entre sus extremos permanece constante.

La propiedad de no tener masa implica que no tienen inercia y que no es necesario aplicarles una fuerza neta para moverlo, sino que simplemente se mueven arrastrados por las masas situadas en sus extremos.

Cuando tiramos de un extremo de un hilo (ideal o real), este experimenta una tensión. Esta es una fuerza debida a la minúscula separación en los átomos del extremo de la cuerda, que a su vez atraen a los átomos situados un poco más allá, y estos tiran de los siguientes, etc. El resultado es que todos los átomos quedan ligeramente separados de sus posiciones de equilibrio y toda el hilo se encuentra en tensión.

En principio, la tensión de un hilo puede ir variando a lo largo de éste. Por ejemplo, imaginemos una cuerda pesada que pende del techo. Los puntos superiores deben soportar una mayor fuerza que los inferiores, y por tanto la tensión será más elevada en los puntos más altos.

Si la cuerda es ideal, sin embargo, la tensión tiene el mismo valor en todos los puntos del hilo. Consideremos un elemento del hilo, de masa $d m$ y longitud $d x$ . De acuerdo con la segunda ley de Newton,

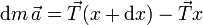
$\mathrm{d}m\,\vec{a}=\vec{T}(x+\mathrm{d}x)-\vec{T}{x}$

ya que el elemento se encuentra sometido a dos tensiones, una por cada extremo, que tiran en sentidos opuestos. Si el hilo es completamente ideal, la masa de elemento es completamente nula y

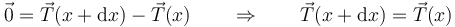
$\vec{0} = \vec{T}(x+\mathrm{d}x)-\vec{T}(x) \qquad\Rightarrow\qquad \vec{T}(x+\mathrm{d}x)= \vec{T}(x)$

Si el hilo se dobla en su camino (por ejemplo, al pasar por una polea también ideal sin masa), la tensión sigue teniendo el mismo módulo en todos los puntos del hilo, aunque su dirección y sentido cambien, por ser siempre tangente al hilo.

2 Péndulo simple

Un ejemplo sencillo de oscilador no lineal es el del péndulo simple. Consideremos una masa $m$ que pende de un punto fijo a través de un hilo ideal, sin masa, y de longitud $l$ . Por acción de la gravedad, la masa oscila en torno al punto más bajo del péndulo.

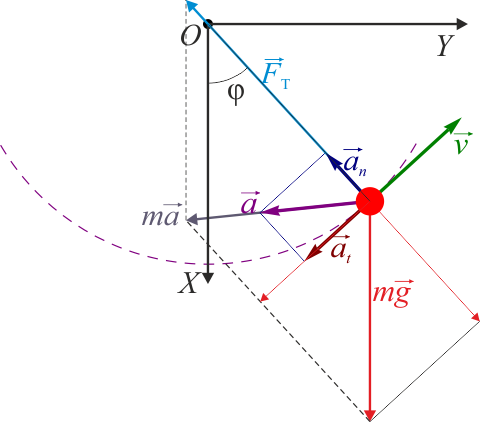
Si usamos coordenadas polares en las que $θ$ es el ángulo con la vertical nos quedan las ecuaciones de movimiento

$m\left(\ddot{\rho}-\rho\dot{\theta}^2\right) = F_\rho\qquad\qquad m(\rho\ddot{\theta}+2\dot{\rho}\dot{\theta})=F_\theta$

Por estar atada a un hilo tenso, la distancia al centro es constante

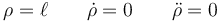
$\rho = \ell\qquad \dot{\rho}=0\qquad \ddot{\rho}=0$

La fuerza radial es la suma de la tensión de la barra, que va hacia adentro, con la componente radial del peso

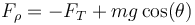
$F_\rho = -F_T + mg\cos(\theta)\,$

mientras que la fuerza acimutal contiene solo la contribución del peso

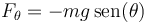
$F_\theta = -mg\,\mathrm{sen}(\theta)$

Esto nos deja con

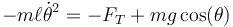
$-m\ell\dot{\theta}^2 = -F_T + mg\cos(\theta)$

y

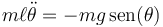
$m \ell \ddot{\theta}=-mg\,\mathrm{sen}(\theta)$

La primera ecuación nos sirve para hallar la tensión una vez que hayamos resuelto la segunda. Esta puede escribirse como

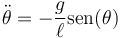
$\ddot{\theta}=-\frac{g}{\ell}\mathrm{sen}(\theta)$

Esta es la ecuación de un oscilador no lineal. Si consideramos que la lenteja del péndulo se separa poco de su posición de equilibrio

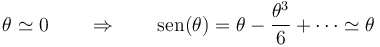
$\theta \simeq 0\qquad\Rightarrow\qquad \mathrm{sen}(\theta)=\theta -\frac{\theta^3}{6}+\cdots \simeq \theta$

y la ecuación del péndulo se reduce a

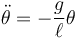
$\ddot{\theta} = -\frac{g}{\ell}\theta$

Esta es la ecuación de un oscilador armónico de frecuencia y periodo

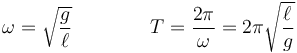
$\omega = \sqrt{\frac{g}{\ell}}\qquad\qquad T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{\ell}{g}}$

Este resultado nos dice que, en primera aproximación, el periodo de un péndulo no depende de la amplitud de las oscilaciones (para grandes amplitudes, esto deja de ser cierto), sino solo de la longitud del péndulo.

Una vez resuelto el problema de hallar $θ(t)$ podemos calcular la tensión del hilo de la ecuación radial

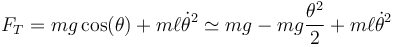
$F_T= mg\cos(\theta) + m \ell\dot{\theta}^2 \simeq mg - mg\frac{\theta^2}{2}+m\ell\dot{\theta}^2$

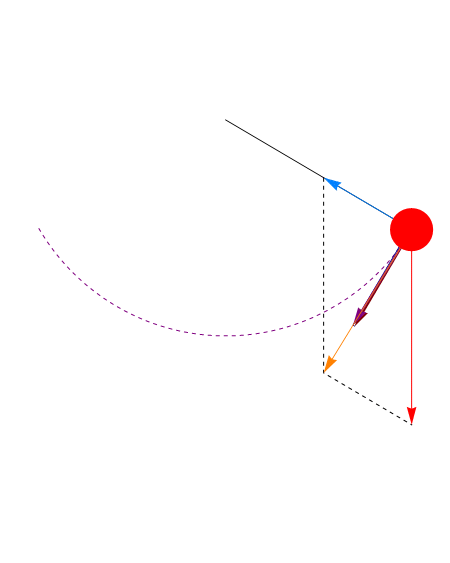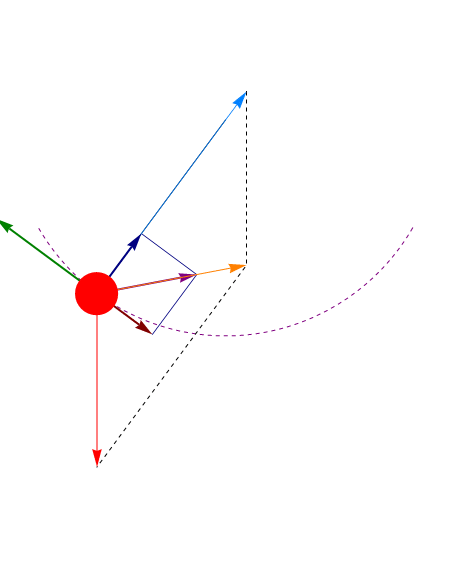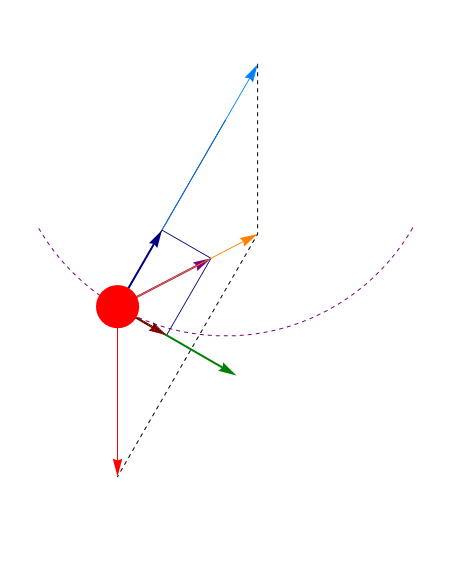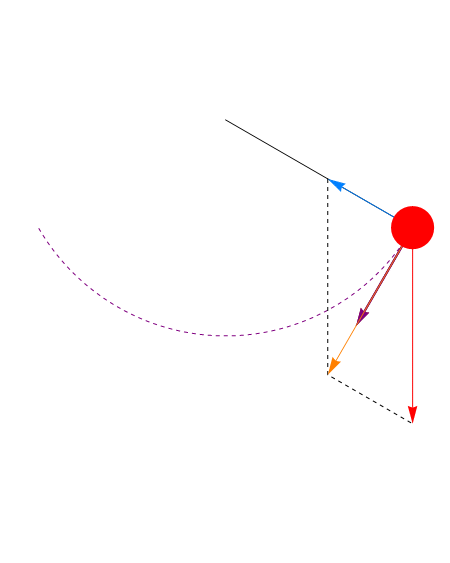
En el punto más bajo ( $θ = 0$ ) esta tensión es mayor que la que habría si el péndulo estuviera en reposo, ya que la fuerza aplicada no es nula, sino que iguala a la masa por la aceleración normal

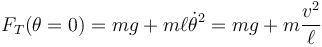
$F_T(\theta=0) = mg + m \ell\dot{\theta}^2 = m g + m\frac{v^2}{\ell}$

3 Máquina de Atwood

Una de las aplicaciones de las tensiones de hilos es el de la máquina de Atwood, formada por dos masas $m 1$ y $m 2$ unidas por un hilo ideal que pasa por una polea también ideal. Cuando se liberan estas masas, la más pesada tira de las más ligera y comienzan a moverse aceleradamente. La cuestión es calcular con qué aceleración lo hacen.

Para la masa $m 1$ , las fuerzas que actúan sobre ella son su peso y la tensión del hilo, de forma que

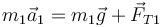
$m_1\vec{a}_1 = m_1\vec{g}+\vec{F}_{T1}$

Puesto que todas las fuerzas son verticales, podemos usar cantidades escalares

$\vec{a}_1 =a \vec{k}\qquad \vec{F}_{T1}=F_T\vec{k}\qquad\vec{g}=-g\vec{k}$

y queda

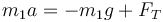
$m_1 a = -m_1g+F_T\,$

Haciendo los mismo para la segunda masa

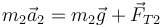
$m_2\vec{a}_2 = m_2\vec{g}+\vec{F}_{T2}$

Por ser la cuerda inextensible, la aceleración con la que se estira por un lado debe ser exactamente igual que con la que se recoge por otro.

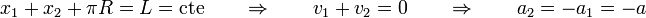
$x_1 + x_2 +\pi R = L=\mathrm{cte}\qquad\Rightarrow\qquad v_1+v_2 = 0\qquad\Rightarrow\qquad a_2=-a_1=-a$

Por otro lado, como el módulo de la tensión del hilo es el mismo a lo largo de todos sus puntos

$\vec{a}_2 = -a\vec{k}\qquad \vec{F}_{T2} = F_T\vec{k}$

lo que nos da la ecuación escalar

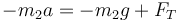
$-m_2a = -m_2g + F_T\,$

Restando las dos ecuaciones obtenemos la aceleración

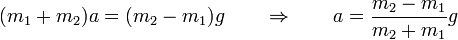
$(m_1+m_2)a = (m_2-m_1)g\qquad\Rightarrow\qquad a = \frac{m_2-m_1}{m_2+m_1}g$

y si queremos la tensión del hilo

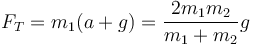
$F_T = m_1(a+g) = \frac{2m_1m_2}{m_1+m_2}g$

La fuerza que debe ejercer el anclaje de la polea la da el que debe compensar las fuerzas que el hilo ejerce sobre ella ahacia abajo. Estas tenmsiones son opuestas a las que se ejercen sobre las masas.

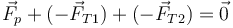
$\vec{F}_p+(-\vec{F}_{T1})+(-\vec{F}_{T2})=\vec{0}$

por lo que

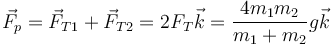
$\vec{F}_p=\vec{F}_{T1}+\vec{F}_{T2} = 2F_T\vec{k}=\frac{4m_1m_2}{m_1+m_2}g\vec{k}$

Vemos que no es simplemente igual al peso de las dos masas, sino que influye el que éstas estén aceleradas.

Péndulos e hilos (GIE)

De Laplace

Contenido

1 Tensión de un hilo

2 Péndulo simple

3 Máquina de Atwood

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES