Cilindro imanado en dirección acimutal

De Laplace

(Diferencias entre revisiones)

Antonio (Discusión | contribuciones)
(Nueva página: Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, [[Campos_vectoriales_e...)
Edición más nueva →

Revisión de 12:56 3 abr 2009

Cuando se tiene un cilindro de un material magnético recorrido por corrientes longitudinales el campo magnético y la imanación van en la dirección acimutal, expresable en cilíndricas o cartesianas como

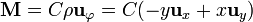
$\mathbf{M}=C\rho\mathbf{u}_\varphi = C(-y\mathbf{u}_x+x\mathbf{u}_y)$

Supongamos un cilindro de radio $R$ y longitud $L$ imanado de esta forma. Las corrientes de magnetización son nulas en el exterior del cilindro, mientras que en el interior puede hallarse su rotacional

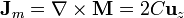
$\mathbf{J}_m = \nabla\times\mathbf{M}=2C\mathbf{u}_z$

Para las corrientes superficiales tenemos

En la base superior 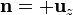$\mathbf{n}=+\mathbf{u}_z$ y

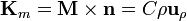
$\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= C\rho\mathbf{u}_\rho\,$

En la base inferior 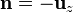$\mathbf{n}=-\mathbf{u}_z$ y

$\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= -C\rho\mathbf{u}_\rho\,$

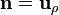
En la cara lateral $\mathbf{n}=\mathbf{u}_\rho$

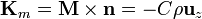
$\mathbf{K}_m = \mathbf{M}\times\mathbf{n}= -C\rho\mathbf{u}_z\,$

Las corrientes de magnetización en este sistema suben por el interior del volumen, van radialmente hacia la superficie exterior por la cara superior, bajan por la cara lateral y vuelven radialmente hacia adentro por la base inferior. El resultado son líneas de corriente cerradas en torno a la imanación.

Cilindro imanado en dirección acimutal

De Laplace

Revisión de 12:56 3 abr 2009

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES