Primera Convocatoria Ordinaria 2020/21 (MR G.I.C.)
De Laplace
(→Barra deslizando sobre apoyo vertical) |
(→Equilibrio de barra con muelle) |
||
| Línea 35: | Línea 35: | ||
==[[ Equilibrio de barra con muelle (Ene. 2021) | Equilibrio de barra con muelle ]]== | ==[[ Equilibrio de barra con muelle (Ene. 2021) | Equilibrio de barra con muelle ]]== | ||
| + | [[Archivo:MRGIC-barraPTV-Enunciado.png|right]] | ||
| + | |||
| + | Una barra de longitud <math>2d</math> está articulada en su punto central en el punto fijo <math>O</math>. El | ||
| + | extremo <math>A</math> se conecta al punto fijo <math>C</math> por un muelle de constante elástica <math>k</math> y longitud | ||
| + | natural nula. Una fuerza <math>\vec{F}=F_0\,\vec{\imath}</math>, con <math>F_0>0</math>, se aplica en el punto <math>B</math>. | ||
| + | No se tiene en cuenta la fuerza de la gravedad. | ||
| + | #Usando el Principio de los Trabajos Virtuales (PTV) (o el de las potencias virtuales, PPV) determina el valor de equilibrio del ángulo <math>\theta</math>. | ||
| + | #Si el ángulo es tal que <math>\,\mathrm{sen}\,{\theta}=3/5</math> y <math>\cos\theta=4/5</math>, determina, usando el Principio de Liberación y el PTV (o el PPV), las componentes de la fuerza de reacción vincular en <math>O</math> (en la base de los ejes de la figura) | ||
última version al 10:24 18 feb 2021
1 Disco articulado en barra con extremo moviéndose en un raíl vertical
Un aro de masa m y radio R (sólido "2") rueda sin deslizar sobre una superficie rugosa
(eje fijo OX1). En el centro del aro se articula una varilla delgada de masa m y longitud
2R (sólido "0"). El otro extremo de la varilla se articula en un pasador que debe moverse en
un raíl fijo vertical. La distancia entre el eje OY1 y el raíl es 4R. La gravedad actúa como se indica
en la figura. Una fuerza 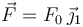 actúa sobre el extremo B de la barra.
actúa sobre el extremo B de la barra.
- Localiza gráficamente los C.I.R. de los tres movimientos relativos del sistema y escribe sus vectores de posición respecto a O.
- Demuestra que existen dos ligaduras de la forma
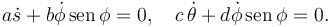 . Encuentra los valores de los coeficientes a,b,c,d.
. Encuentra los valores de los coeficientes a,b,c,d.
- Escribe las reducciones cinemáticas de los movimientos absolutos de los dos sólidos en sus centros de masas respectivos. Deben quedar en función de φ y
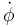 .
.
- Calcula la energía cinética total del sistema.
- Dibuja los diagramas de fuerzas de los dos sólidos.
- Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el movimiento y las reacciones vinculares. No es necesario hacer las derivadas temporales al aplicar los teoremas.
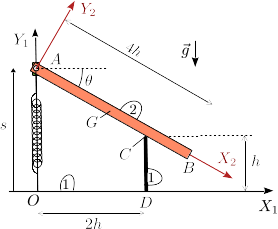
2 Barra deslizando sobre apoyo vertical
Una barra de masa m y longitud 4h (sólido "2") está articulada en un extremo (punto A) en un pasador que puede deslizar sobre el eje fijo OY1. El otro extremo de la barra se apoya en un apoyo vertical, de modo que el punto C de la barra puede deslizar sin rozamiento sobre el apoyo. Un muelle de constante elástica k y longitud natural 2h conecta el extremo A de la barra con el punto O. La gravedad actúa como se indica en la figura.
- Encuentra la reducción cinemática del movimiento {21} expresada en la base del sólido "1" y en función de las coordenadas {s,θ} y sus derivadas temporales. ¿Como es la ligadura cinemática que relaciona estas coordenadas?
- Calcula las siguientes magnitudes cinéticas del sólido "2":
 ,
, 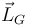 , T, U. Expresa los resultados usando las coordenadas {s,θ} y sus derivadas temporales.
, T, U. Expresa los resultados usando las coordenadas {s,θ} y sus derivadas temporales.
- Supongamos que la función de Lagrange y el vínculo cinemático tienen esta forma ( A, B, C, D y E son constantes dadas)

Aplicando la técnica de los multiplicadores de Lagrange, encuentra las ecuaciones de movimiento.
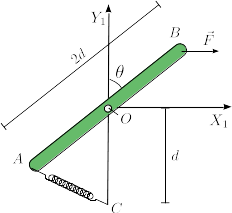
3 Equilibrio de barra con muelle
Una barra de longitud 2d está articulada en su punto central en el punto fijo O. El
extremo A se conecta al punto fijo C por un muelle de constante elástica k y longitud
natural nula. Una fuerza 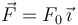 , con F0 > 0, se aplica en el punto B.
No se tiene en cuenta la fuerza de la gravedad.
, con F0 > 0, se aplica en el punto B.
No se tiene en cuenta la fuerza de la gravedad.
- Usando el Principio de los Trabajos Virtuales (PTV) (o el de las potencias virtuales, PPV) determina el valor de equilibrio del ángulo θ.
- Si el ángulo es tal que
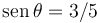 y cosθ = 4 / 5, determina, usando el Principio de Liberación y el PTV (o el PPV), las componentes de la fuerza de reacción vincular en O (en la base de los ejes de la figura)
y cosθ = 4 / 5, determina, usando el Principio de Liberación y el PTV (o el PPV), las componentes de la fuerza de reacción vincular en O (en la base de los ejes de la figura)