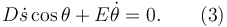De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

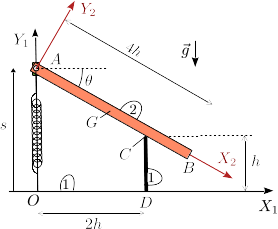
Una barra de masa $m$ y longitud 4h (sólido "2") está articulada en un extremo (punto $A$ ) en un pasador que puede deslizar sobre el eje fijo $O Y 1$ . El otro extremo de la barra se apoya en un apoyo vertical, de modo que el punto $C$ de la barra puede deslizar sin rozamiento sobre el apoyo. Un muelle de constante elástica $k$ y longitud natural $2 h$ conecta el extremo $A$ de la barra con el punto $O$ . La gravedad actúa como se indica en la figura.

Encuentra la reducción cinemática del movimiento {21} expresada en la base del sólido "1" y en función de las coordenadas ${s,θ}$ y sus derivadas temporales. ¿Como es la ligadura cinemática que relaciona estas coordenadas?
Calcula las siguientes magnitudes cinéticas del sólido "2": 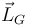$\vec{C}$ , $\vec{L}_G$ , $T$ , $U$ . Expresa los resultados usando las coordenadas ${s,θ}$ y sus derivadas temporales.
Supongamos que la función de Lagrange y el vínculo cinemático tienen esta forma ( $A$ , $B$ , $C$ , $D$ y $E$ son constantes dadas)

$L = A\dot{s}^2 + B\dot{\theta}^2 + C \dot{s}\,\dot{\theta}, \qquad g = D\dot{s}\cos{\theta} + E\dot{\theta}=0.$

Aplicando la técnica de los multiplicadores de Lagrange, encuentra las ecuaciones de movimiento.

2 Solución

2.1 Reducción cinemática

Observando el dibujo vemos que

$\vec{\omega}_{21} = -\dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,A}_{21} = \dot{s}\,\vec{\jmath}_1.$

Al ser un movimiento plano el vector rotación sólo tiene componente en el eje $Z$ .

La barra desliza sobre el apoyo vertical en $C$ . Esto implica que 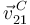$\vec{v}^{\,C}_{21}$ debe ser paralela a la propia barra

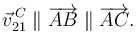
$\vec{v}^{\,C}_{21} \parallel \overrightarrow{AB} \parallel \overrightarrow{AC}.$

Así pues el sistema tiene un grado de libertad. Aplicamos Chasles para encontrar la expresión matemática del vínculo

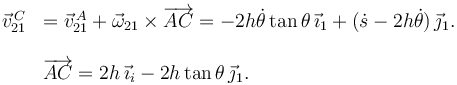
$\begin{array}{ll} \vec{v}^{\,C}_{21} & = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AC} =-2h\dot{\theta}\tan\theta\,\vec{\imath}_1 + (\dot{s}-2h\dot{\theta})\,\vec{\jmath}_1. \\ &\\ & \overrightarrow{AC} = 2h\,\vec{\imath}_i -2h\tan\theta\,\vec{\jmath}_1. \end{array}$

Aplicamos la ligadura en $C$

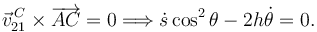
$\vec{v}^{\,C}_{21}\times\overrightarrow{AC} = 0 \Longrightarrow \dot{s}\cos^2\theta - 2h\dot{\theta}=0.$

Otra forma de llegar a esta ligadura es de forma geométrica. Observando el dibujo vemos que

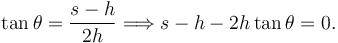
$\tan\theta = \dfrac{s-h}{2h} \Longrightarrow s-h - 2h\tan\theta = 0.$

Derivando respecto al tiempo obtenemos la ligadura cinemática anterior.

2.2 Cinética

Cantidad de movimiento

La velocidad del centro de masas de la barra es

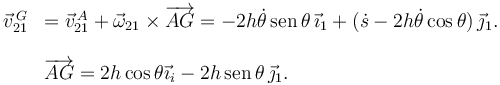
$\begin{array}{ll} \vec{v}^{\,G}_{21} & = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG} =-2h\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + (\dot{s}-2h\dot{\theta}\cos\theta)\,\vec{\jmath}_1. \\ &\\ & \overrightarrow{AG} = 2h\cos\theta\vec{\imath}_i -2h\,\mathrm{sen}\,\theta\,\vec{\jmath}_1. \end{array}$

Y la cantidad de movimiento es

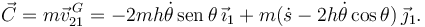
$\vec{C} = m\vec{v}^{\,G}_{21} = -2mh\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + m(\dot{s}-2h\dot{\theta}\cos\theta)\,\vec{\jmath}_1.$

Momento angular en el centro de masas

Como es un movimiento plano y es el centro de masas de la barra podemos usar la expresión

$\vec{L}_G = I_G\vec{\omega}_{21} = -\dfrac{4}{3}mh^2\dot{\theta}\,\vec{k}. \qquad \qquad (I_G = m(4h)^2/12 = 4mh^2/3)$

Energía cinética

La calculamos pasando por el centro de masas. Al ser un movimiento plano

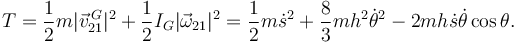
$T = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}I_G|\vec{\omega}_{21}|^2 = \dfrac{1}{2}m\dot{s}^2 + \dfrac{8}{3}mh^2\dot{\theta}^2 -2mh\dot{s}\dot{\theta}\cos\theta.$

Energía potencial

La energía potencial elástica del muelle es

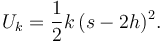
$U_k = \dfrac{1}{2}k\,(s-2h)^2.$

La energía potencial gravitatoria es (tomando como referencia la altura del eje $X 1$ )

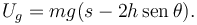
$U_g = mg(s-2h\,\mathrm{sen}\,\theta).$

La energía potencial total es

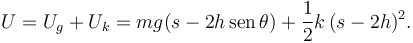
$U = U_g + U_k = mg(s-2h\,\mathrm{sen}\,\theta) + \dfrac{1}{2}k\,(s-2h)^2.$

2.3 Multiplicadores de Lagrange

Siguiendo el enunciado suponemos que la función de Lagrange y el vínculo cinemático son

$L = A\dot{s}^2 + B\dot{\theta}^2 + C \dot{s}\,\dot{\theta}, \qquad g = D\dot{s}\cos{\theta} + E\dot{\theta}=0.$

Como hay un vínculo cinemático hay que introducir un multiplicador de Lagrange. De este modo podemos seguir trabajando con las coordenadas ${s,θ}$ , aunque el sistema tenga sólo un grado de libertad. Las ecuaciones de Lagrange son como sigue

Ecuación para $s$

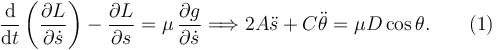
$\dfrac{\mathrm{d}}{\mathrm{d}t} \left(\dfrac{\partial L}{\partial\dot{s}}\right) - \dfrac{\partial L}{\partial s} = \mu\,\dfrac{\partial g}{\partial \dot{s}} \Longrightarrow 2A\ddot{s} + C\ddot{\theta} = \mu D\cos\theta. \qquad (1)$

Ecuación para $θ$

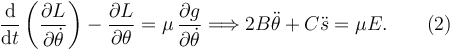
$\dfrac{\mathrm{d}}{\mathrm{d}t} \left(\dfrac{\partial L}{\partial\dot{\theta}}\right) - \dfrac{\partial L}{\partial \theta} = \mu\,\dfrac{\partial g}{\partial \dot{\theta}} \Longrightarrow 2B\ddot{\theta} + C\ddot{s} = \mu E. \qquad (2)$

Ecuación del vínculo

La tercera ecuación es el propio vínculo

$D\dot{s}\cos\theta + E\dot{\theta} = 0. \qquad (3)$

Barra deslizando sobre apoyo vertical (Ene. 2021)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática

2.2 Cinética

2.3 Multiplicadores de Lagrange

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES