Problemas de herramientas matemáticas (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Arco capaz== Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores <math>\overrightarr…') |
(→Arco capaz) |
||
| Línea 6: | Línea 6: | ||
[[Arco capaz (GIOI)|Solución]] | [[Arco capaz (GIOI)|Solución]] | ||
| + | |||
| + | ==Coseno y seno de una diferencia== | ||
| + | A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos. | ||
| + | |||
| + | <center>[[Archivo:diferencia-angulos.png]]</center> | ||
| + | |||
| + | [[Coseno y seno de una diferencia|Solución]] | ||
Revisión de 15:11 7 oct 2019
1 Arco capaz
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores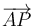 
y
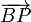son ortogonales.
Inversamente, sean A, B y P tres puntos tales que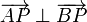 
. Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.
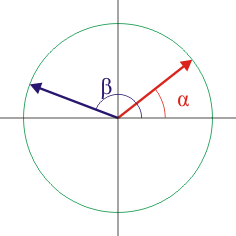
2 Coseno y seno de una diferencia
A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.
