Revisión de 18:23 30 sep 2015

Contenido

1 Problemas del boletín

1 Problemas del boletín

1.1 Giro de un triedro

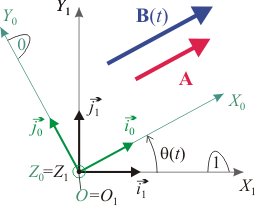
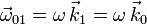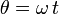Los triedros $O 1 X 1 Y 1 Z 1$ y $O X 0 Y 0 Z 0$ están definidos de modo que sus orígenes y los ejes $O 1 Z 1$ coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme $\vec{\omega}_{01} = \omega\,\vec{k}_1 =\omega\,\vec{k}_0$ , de modo que el ángulo $θ$ indicado en la figura es $\theta = \omega\, t$ .

Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1".
Dado el vector 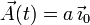$\vec{A}(t) = a\,\vec{\imath}_0$ calcula

$\left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_1 \qquad\qquad \left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_0$

Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1").
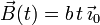
Haz el mismo cálculo para el vector $\vec{B}(t) = b\,t\,\vec{\imath}_0$

1.2 Coche sobre una plataforma circular

Una plataforma circular gira alrededor de un eje perpendicular a ella que pasa por su centro con velocidad angular uniforme $ω$ . Un coche se mueve radialmente desde el centro de la plataforma hacia fuera con velocidad uniforme $v c$ . Encuentra la expresión de la velocidad del coche visto desde la plataforma y desde un observador en reposo absoluto. Describe las trayectorias que describe el coche para cada uno de estos observadores.

Ayuda

$\begin{array}{ccc} \displaystyle\int t\,\,\mathrm{sen}\,(\omega t)\mathrm{d} t = -\dfrac{t}{\omega}\cos(\omega t) + \dfrac{1}{\omega^2}\,\mathrm{sen}\,(\omega t)& \qquad &\displaystyle\int t\,\cos(\omega t)\mathrm{d} t = \dfrac{t}{\omega}\,\mathrm{sen}\,(\omega t) + \dfrac{1}{\omega^2}\cos(\omega t) \end{array}$

1.3 Disco engarzado en otro disco

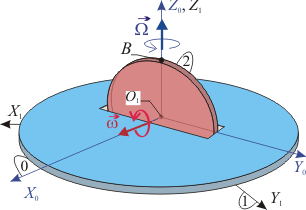
En la figura se muestra un disco de radio $R$ (sólido "2"), que gira con velocidad angular $ω 20 (t) = ω$ , constante, alrededor del eje perpendicular a él, $O 1 X 0$ . Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante $ω 01 (t) = Ω$ , alrededor del eje vertical $O 1 Z 1$ de un sistema de referencia fijo $O 1 X 1 Y 1 Z 1$ (sólido "1"). Determina las magnitudes cinemáticas $\vec{v}^B_{21}$ y $\vec{a}^B_{21}$ en el instante representado en la figura.