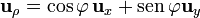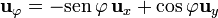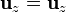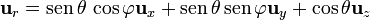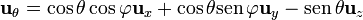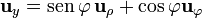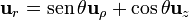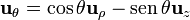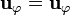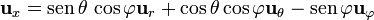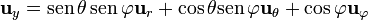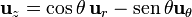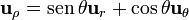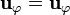Relaciones entre las bases vectoriales
De Laplace
(Diferencias entre revisiones)
(→De cartesianas a cilíndricas) |
|||
| Línea 1: | Línea 1: | ||
| - | ==De la [[Coordenadas cartesianas. Base vectorial|base cartesiana]] a la [[Coordenadas cilíndricas. Base vectorial|base | + | ==De la [[Coordenadas cartesianas. Base vectorial|base cartesiana]] a la [[Coordenadas cilíndricas. Base vectorial|base de cilíndricas]]== |
*<math>\mathbf{u}_\rho = \cos\varphi\,\mathbf{u}_{x} + \mathrm{sen}\,\varphi \mathbf{u}_{y} | *<math>\mathbf{u}_\rho = \cos\varphi\,\mathbf{u}_{x} + \mathrm{sen}\,\varphi \mathbf{u}_{y} | ||
| Línea 9: | Línea 9: | ||
*<math>\mathbf{u}_z=\mathbf{u}_z\,</math> | *<math>\mathbf{u}_z=\mathbf{u}_z\,</math> | ||
| - | ==De [[Coordenadas cartesianas. Base vectorial| | + | ==De la [[Coordenadas cartesianas. Base vectorial|base cartesiana]] a la [[Coordenadas esféricas. Base vectorial|base de esféricas]]== |
*<math>\mathbf{u}_{r}=\mathrm{sen}\,\theta\,\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z} | *<math>\mathbf{u}_{r}=\mathrm{sen}\,\theta\,\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z} | ||
| Línea 19: | Línea 19: | ||
</math> | </math> | ||
| - | ==De [[Coordenadas cilíndricas. Base vectorial|cilíndricas]] a [[Coordenadas cartesianas. Base vectorial| | + | ==De la [[Coordenadas cilíndricas. Base vectorial|base de cilíndricas]] a la [[Coordenadas cartesianas. Base vectorial|base cartesiana]]== |
*<math>\mathbf{u}_x = \cos\varphi\,\mathbf{u}_{\rho} - \mathrm{sen}\,\varphi \mathbf{u}_{\varphi} | *<math>\mathbf{u}_x = \cos\varphi\,\mathbf{u}_{\rho} - \mathrm{sen}\,\varphi \mathbf{u}_{\varphi} | ||
| Línea 29: | Línea 29: | ||
*<math>\mathbf{u}_z=\mathbf{u}_z\,</math> | *<math>\mathbf{u}_z=\mathbf{u}_z\,</math> | ||
| - | ==De [[Coordenadas cilíndricas. Base vectorial|cilíndricas]] a [[Coordenadas esféricas. Base vectorial| | + | ==De la [[Coordenadas cilíndricas. Base vectorial|base de cilíndricas]] a la [[Coordenadas esféricas. Base vectorial|base de esférica]]== |
*<math>\mathbf{u}_{r}= \mathrm{sen}\,\theta\mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z}</math> | *<math>\mathbf{u}_{r}= \mathrm{sen}\,\theta\mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z}</math> | ||
| Línea 37: | Línea 37: | ||
*<math>\mathbf{u}_\varphi = \mathbf{u}_\varphi</math> | *<math>\mathbf{u}_\varphi = \mathbf{u}_\varphi</math> | ||
| - | ==De [[Coordenadas esféricas. Base vectorial|esféricas]] a [[Coordenadas cartesianas. Base vectorial| | + | ==De la [[Coordenadas esféricas. Base vectorial|base de esféricas]] a la [[Coordenadas cartesianas. Base vectorial|base cartesiana]]== |
*<math>\mathbf{u}_{x}=\mathrm{sen}\,\theta\,\cos\varphi\mathbf{u}_{r}+\cos\theta\cos\varphi\mathbf{u}_{\theta}-\mathrm{sen}\,\varphi\mathbf{u}_{\varphi}</math> | *<math>\mathbf{u}_{x}=\mathrm{sen}\,\theta\,\cos\varphi\mathbf{u}_{r}+\cos\theta\cos\varphi\mathbf{u}_{\theta}-\mathrm{sen}\,\varphi\mathbf{u}_{\varphi}</math> | ||
| Línea 45: | Línea 45: | ||
*<math>\mathbf{u}_z = \cos\theta\,\mathbf{u}_{r} - \mathrm{sen}\,\theta \mathbf{u}_{\theta}</math> | *<math>\mathbf{u}_z = \cos\theta\,\mathbf{u}_{r} - \mathrm{sen}\,\theta \mathbf{u}_{\theta}</math> | ||
| - | ==De [[Coordenadas esféricas. Base vectorial|esféricas]] a [[Coordenadas cilíndricas. Base vectorial|cilíndricas]]== | + | ==De la [[Coordenadas esféricas. Base vectorial|base de esféricas]] a la [[Coordenadas cilíndricas. Base vectorial|base de cilíndricas]]== |
*<math>\mathbf{u}_{\rho}=\mathrm{sen}\,\theta\mathbf{u}_{r}+\cos\theta\mathbf{u}_{\theta}</math> | *<math>\mathbf{u}_{\rho}=\mathrm{sen}\,\theta\mathbf{u}_{r}+\cos\theta\mathbf{u}_{\theta}</math> | ||
Revisión de 10:14 22 nov 2007
1 De la base cartesiana a la base de cilíndricas
2 De la base cartesiana a la base de esféricas
3 De la base de cilíndricas a la base cartesiana
4 De la base de cilíndricas a la base de esférica
5 De la base de esféricas a la base cartesiana
6 De la base de esféricas a la base de cilíndricas
A su vez, todas estas expresiones pueden expresarse en los diferentes sistemas de coordenadas, sustituyendo la relación entre los distintos sistemas de coordenadas