Movimiento de un péndulo
De Laplace
(Página creada con '==Enunciado== Tenemos un péndulo simple formado por una lenteja de 0.5 kg que cuelga de una varilla rígida de masa despreciable y 1.20 m de longitud. # Si se se…') |
|||
| Línea 6: | Línea 6: | ||
==Introducción== | ==Introducción== | ||
| + | El péndulo simple se analiza de forma general en el apartado teórico del tema de de [[Péndulos_e_hilos_(GIE)#P.C3.A9ndulo_simple|dinámica]] y se vuelve a revisar en el de [[Rapidez_y_tensión_de_un_péndulo|energía y leyes de conservación]]. Aquí solo veremos los resultados concretos para este caso. | ||
==Rapidez y periodo== | ==Rapidez y periodo== | ||
| + | Cuando la amplitud de las oscilaciones es pequeña, el péndulo sigue aproximadamente un movimiento armónico de ecuación | ||
| + | |||
| + | <center><math>\ddot{\varphi}=-\frac{g}{l}\varphi</math></center> | ||
| + | |||
| + | Si la partícula parte del reposo con un ángulo de separación <math>\varphi_0</math>, la solución para todo instante es | ||
| + | |||
| + | <center><math>\varphi=\varphi_0\cos(\Omega t) \qquad\qquad\Omega = \sqrt{\frac{g}{l}}</math></center> | ||
| + | |||
| + | La velocidad angular con la que se mueve la lenteja respecto al punto de anclaje es | ||
| + | |||
| + | <center><math>\dot{\varphi}=-\varphi_0\Omega\,\mathrm{sen}(\Omega t)</math></center> | ||
| + | |||
| + | El punto más bajo corresponde a <math>\varphi=0</math> lo cual ocurre en un cierto instante <math>t_1</math> dado por | ||
| + | |||
| + | <center><math>0=\varphi = \varphi_0\cos(\Omega t_1)\qquad \Rightarrow\qquad\Omega t_1 = \rac{\pi}{2}</math></center> | ||
| + | |||
| + | y para ese instante el seno vale la unidad, por lo que | ||
| + | |||
| + | <center><math>\dot{\varphi}=-\varphi_0\Omega</math></center> | ||
| + | |||
| + | Larapidez de la partícula en ese instante es igual a | ||
| + | |||
| + | <center><math>|\vec{v}|=|l\dot{\varphi}|=l\varphi_0\Omega = \varphi_0\sqrt{gl}</math></center> | ||
| + | |||
| + | siendo su valor numérico | ||
| + | |||
| + | <center><math>|\vec{v}|=\frac{5\pi}{180}\sqrt{9.81\times 1.20}\,\frac{\mathrm{m}}{\mathrm{s}} = 0.30\,\mathrm{s}</math></center> | ||
| + | |||
| + | El periodo de oscilación será cuádruple de este tiempo, es decir, <math>T = 1.20\,\mathrm{s}</math> | ||
==Tensión del hilo== | ==Tensión del hilo== | ||
==Comparación de dos péndulos== | ==Comparación de dos péndulos== | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 19:55 23 ene 2015
Contenido |
1 Enunciado
Tenemos un péndulo simple formado por una lenteja de 0.5 kg que cuelga de una varilla rígida de masa despreciable y 1.20 m de longitud.
- Si se separa la lenteja de la vertical un ángulo de 5° y se suelta desde el reposo, ¿con qué rapidez pasa la masa por el punto más bajo? ¿Cuánto tiempo tarda en llegar a esta posición?
- ¿Cuánto vale la tensión de la varilla en el momento de soltar la masa? ¿Y en el punto más bajo?
- Suponga que se ajusta un reloj suponiendo que se usa el péndulo anterior, pero resulta que en realidad la varilla mide 115\,cm. El reloj ¿atrasa o adelanta? ¿Cuánto cada día?
2 Introducción
El péndulo simple se analiza de forma general en el apartado teórico del tema de de dinámica y se vuelve a revisar en el de energía y leyes de conservación. Aquí solo veremos los resultados concretos para este caso.
3 Rapidez y periodo
Cuando la amplitud de las oscilaciones es pequeña, el péndulo sigue aproximadamente un movimiento armónico de ecuación
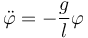
Si la partícula parte del reposo con un ángulo de separación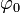 
, la solución para todo instante es
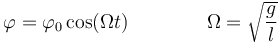
La velocidad angular con la que se mueve la lenteja respecto al punto de anclaje es
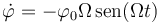
El punto más bajo corresponde a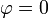 
lo cual ocurre en un cierto instante t1 dado por
y para ese instante el seno vale la unidad, por lo que
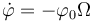
Larapidez de la partícula en ese instante es igual a
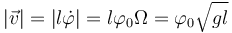
siendo su valor numérico
El periodo de oscilación será cuádruple de este tiempo, es decir, 
