|
|
| Línea 1: |
Línea 1: |
| | [[F1 GIA SPC 2013, Masa subiendo por rampa | Masa subiendo por rampa]] | | [[F1 GIA SPC 2013, Masa subiendo por rampa | Masa subiendo por rampa]] |
| - | | + | [[Imagen:F1_GIA_SPC_2013_masa_rampa.png|center]] |
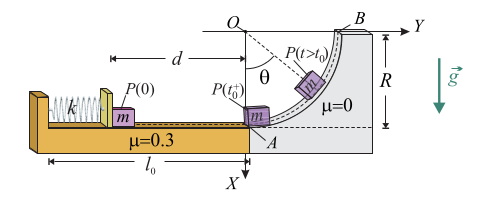
| - | En la figura se muestra el esquema de un sistema mecánico formado por un lanzador de longitud <math>l_0</math>, conectado a una rampa ascendente que consiste en un cuadrante de superficie cilíndrica de radio <math>R</math>. El lanzador está compuesto por un plano horizontal rugoso y, paralelo a ́este, un resorte de longitud natural <math>l_0</math> y constante recuperadora <math>k</math>, con un extremo fijo en el lanzador. El otro extremo impulsa a la partícula <math>P</math> cuando el resorte se halla comprimido. El contacto entre la partícula y el plano del lanzador
| + | |
| - | está caracterizado por un coeficiente de rozamiento dinámico de valor <math>\mu = 0.3</math>. Una vez que la partícula abandona el lanzador y entra en contacto con la superficie de la rampa, el rozamiento puede considerarse
| + | |
| - | despreciable.
| + | |
| - | #Si <math>K_0</math> es el valor de la energía cinética de una partícula de masa <math>m</math>, en el instante <math>t = t_0^+ </math> en que esta entra en la rampa ascendente (punto <math>A</math>) ¿cómo está relacionada la energía cinética de la partícula con su posición en la rampa, dada por el valor del ́angulo <math>\theta</math> indicado en al figura?
| + | |
| - | #¿Qué distancia mínima <math>(d = d_{min} )</math> hay que comprimir el resorte para que una partícula de masa <math>m = k R/g</math> pueda completar el recorrido sobre la rampa, deteniéndose instantáneamente en el punto <math>B</math>?
| + | |
| - | #Considerando que el resorte estaba comprimido la distancia <math>d_{min}</math> para que la partícula de la cuestión anterior pueda alcanzar el extremo <math>B</math>, ¿cuanto valen los módulos de la velocidad y la aceleración instantánea de la partícula en el instante <math>t = t_0^+</math> , cuando acaba de entrar en la rampa (punto <math>A</math>)?
| + | |
| - | #Cuando se procede al lanzamiento de la partícula y ́esta pasa del lanzador plano horizontal en <math>t=t_0^-</math>, a la rampa <math>t=t_0^+ </math>, ¿que le ocurre a la componente de la fuerza de reacción vincular que es perpendicular a las superficies por las que desliza (es decir, la componente normal lisa asociada al vínculo geométrico)
| + | |
| | | | |
| | [[F1 GIA SPC 2013, Satélite girando alrededor de la Tierra | Satélite girando alrededor de la Tierra]] | | [[F1 GIA SPC 2013, Satélite girando alrededor de la Tierra | Satélite girando alrededor de la Tierra]] |
| | | | |
| - | Un satélite meteorológico realiza un movimiento circular uniforme en torno a la Tierra, describiendo ́una órbita circular a una altura de 850 km sobre la superficie. Considerando que la única fuerza significativa que actúa sobre el satélite es la debida al campo gravitatorio terrestre, ¿cuántas vueltas a la Tierra efectúa al cabo del día?
| |
| - | [[Imagen:F1_GIA_SPC_2013_masa_rampa.png|center]]
| |
| | | | |
| | [[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] | | [[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] |
| - |
| |
| - | Un disco de radio <math>\sqrt{2}R </math> y espesor no despreciable (sólido "2") se mueve respecto de un plano fijo <math>\Pi_1\equiv OX_1Y_1 </math> (sólido "1"). En cada instante, un punto del perímetro de la base inferior del disco está en contacto con el plano <math>\Pi_1 </math>, mientras que el diametralmente opuesto, se apoya sobre el eje fijo <math>OZ_1 </math>. En todo momento, las bases del disco forman un ángulo <math>\pi/4 </math> con el plano <math>\Pi_1 </math>. El movimiento del disco es tal que rueda sin deslizar sobre dicho plano, en el punto de contacto <math>A </math>. Además, el centro <math>C </math> de la base
| |
| - | inferior realiza un movimiento circular de radio <math>R </math> en torno al eje <math>OZ_1 </math>, en sentido horario y con velocidad de módulo constante <math>v_0 </math>. Para analizar el movimiento, se sugiere utilizar un sólido ("0") consistente en un sistema de referencia <math>OX_0Y_0Z_0 </math> tal que <math>OZ_0 = OZ_1 </math> en todo instante y que se mueve de manera que el eje <math>CC' </math> del disco (cuya prolongación pasa por <math>O </math>) se encuentra en reposo en el plano <math>OY_0Z_0 </math>.
| |
| - | #Trace los ejes de rotación de los movimientos {01}, {20} y {21} en el instante representado e identifique los tipos de movimiento.
| |
| - | #Encuentre la reducción cinemática y su derivada para el movimiento {21}.
| |
| - | [[Imagen:F1_GIA_SPC_2013_disco_rotando_barra_vertical_enunciado.png|center]]
| |