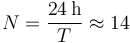F1 GIA SPC 2013, Satélite girando alrededor de la Tierra
De Laplace
1 Enunciado
Un satélite meteorológico realiza un movimiento circular uniforme en torno a la Tierra, describiendo ́una órbita circular a una altura de 850 km sobre la superficie. Considerando que la única fuerza significativa que actúa sobre el satélite es la debida al campo gravitatorio terrestre, ¿cuántas vueltas a la Tierra efectúa al cabo del día?
2 Solución
Si el satélite realiza un movimiento circular uniforme, su aceleración es puramente normal y vale
as = ω2Rs
Donde ω es la velocidad angular y Rs es el radio de la órbita del satélite respecto al centro de la Tierra, es decir
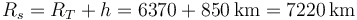
Por otro lado, si la única fuerza que actúa sobre el satélite es la gravedad terrestre, la segunda Ley de Newton nos dice
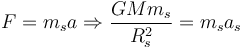
La masa del satélite se va y nos queda que la velocidad angular es
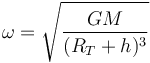
El período de rotación del satélite es
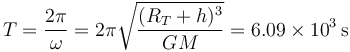
El número de vueltas que da es la duración del día dividido por este valor T