Primera convocatoria 2012/13 (F2GIA)
De Laplace
(→Sistema electrostático formado por cuatro discos conductores) |
|||
| Línea 7: | Línea 7: | ||
# Considere el caso concreto en que el radio de los discos es de <math>36\,\mathrm{mm}</math> y la distancia <math>d=0.4\,\mathrm{mm}</math>. Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico <math>E_\mathrm{rup}^\mathrm{air}=3\,\mathrm{kV}/\mathrm{mm}</math>, determine la diferencia de potencial máxima, <math>V_\mathrm{max}</math>, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor <math>V_\mathrm{max}</math>? | # Considere el caso concreto en que el radio de los discos es de <math>36\,\mathrm{mm}</math> y la distancia <math>d=0.4\,\mathrm{mm}</math>. Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico <math>E_\mathrm{rup}^\mathrm{air}=3\,\mathrm{kV}/\mathrm{mm}</math>, determine la diferencia de potencial máxima, <math>V_\mathrm{max}</math>, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor <math>V_\mathrm{max}</math>? | ||
# Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica <math>\kappa=7</math> y campo de ruptura <math>E_\mathrm{rup}^\mathrm{por}=5.7\,\mathrm{kV}/\mathrm{mm}</math>, ¿cuál será el valor de <math>V_\mathrm{max}</math> y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema? | # Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica <math>\kappa=7</math> y campo de ruptura <math>E_\mathrm{rup}^\mathrm{por}=5.7\,\mathrm{kV}/\mathrm{mm}</math>, ¿cuál será el valor de <math>V_\mathrm{max}</math> y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema? | ||
| + | |||
| + | |||
| + | ==[[Energía_interna,_calor_y_trabajo_en_proceso_cíclico,_F2_GIA_(Jun,_2013)|Energía interna, calor y trabajo en proceso_cíclico]]== | ||
| + | Una cierta cantidad de gas monoatómico ideal contenida en un recipiente hermético realiza el ''proceso cíclico'' representado en el diagrama <math>P-V</math> de la figura y que se describe a continuación: | ||
| + | |||
| + | [[Archivo:proceso_ciclico_0.gif|right]]En el estado inicial de equilibrio “A” ocupa un volumen <math>V_0</math>, a una presión <math>P_0</math>, en equilibrio térmico con un entorno que se encuentra a una temperatura <math>T_0</math>. En primer lugar, el sistema experimenta una compresión isoterma “1”, por el cuál el gas reduce su volumen a la mitad del valor inicial, pero manteniendo constante la temperatura <math>T_0</math>. Una vez alcanzado el estado “B”, el sistema verifica una expansión isóbara “2” (a presión constante) hasta el estado “C”, para recuperar el volumen <math>V_0</math> del estado inicial. Finalmente, en un último proceso isócoro “3” (a volumen constante), se reduce la presión del sistema hasta el valor inicial <math>P_0</math>, alcanzando de nuevo el estado “A”. El proceso cíclico se realiza de manera que pueda considerarse que el gas se encuentra, en todo momento, en equilibrio termodinámico. | ||
| + | |||
| + | # De manera razonada y sin necesidad de realizar cálculos, qué puede decir acerca de las variaciones de energía interna en cada uno de los tres procesos parciales que constituyen el proceso cíclico descrito. | ||
| + | # Determine los valores de presión, volumen y temperatura del sistema en los estados “B” y “C”, en función de los valores iniciales. | ||
| + | # Para cada uno de los procesos parciales, indique de manera razonada el “sentido” en que se verifican las transferencias de calor y trabajo. Indique, asimismo, cómo es la transferencia neta de calor y trabajo en el proceso completo. | ||
| + | # Calcule el rendimiento del ciclo, definido como la relación entre el trabajo neto (en valor absoluto) transferido en el proceso cíclico, y la cantidad de calor absorbido <math>Q_\mathrm{in}</math> (es decir, sólo el que ''entra'' en el sistema). | ||
[[Categoría:Problemas de examen F2 GIA]] | [[Categoría:Problemas de examen F2 GIA]] | ||
Revisión de 00:30 11 sep 2013
1 Sistema electrostático formado por cuatro discos conductores
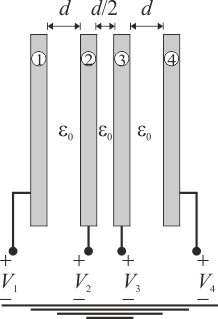
Un sistema de conductores está formado por cuatro discos metálicos idénticos, de sección S, colocados con sus respectivas superficies en planos paralelos y con sus centros en el mismo eje perpendicular a los discos. Las superficies enfrentadas de los dos discos centrales, “2” y “3”, están separadas una distancia d / 2, mientras que sus otras superficies se mantienen a una distancia d de las de los discos “1” y “4”, colocados en los extremos del sistema. El valor de d es lo suficientemente pequeño frente al diámetro y grosor de los discos como para poder considerar que cada par de superficies conductoras enfrentadas se encuentran en influencia total, formando así un condensador plano paralelo relleno de aire.
- Obtenga las expresiones para la carga eléctrica total en cada uno de los discos en función de los parámetros geométricos y de los valores del potencial electrostático en los discos.
- Los discos “1” y “3” se conectan mediante un cable conductor ideal, formando el conductor “A”, e igualmente se hace con “2” y “4” para forma el “B”. Justifique por qué los conductores surgidos de estas asociaciones forman un condensador y calcule su capacidad eléctrica equivalente.
- Considere el caso concreto en que el radio de los discos es de
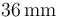 y la distancia
y la distancia 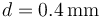 . Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico
. Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico 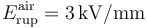 , determine la diferencia de potencial máxima, Vmax, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor Vmax?
, determine la diferencia de potencial máxima, Vmax, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor Vmax?
- Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica κ = 7 y campo de ruptura
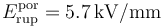 , ¿cuál será el valor de Vmax y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema?
, ¿cuál será el valor de Vmax y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema?
2 Energía interna, calor y trabajo en proceso_cíclico
Una cierta cantidad de gas monoatómico ideal contenida en un recipiente hermético realiza el proceso cíclico representado en el diagrama P − V de la figura y que se describe a continuación:
En el estado inicial de equilibrio “A” ocupa un volumen V0, a una presión P0, en equilibrio térmico con un entorno que se encuentra a una temperatura T0. En primer lugar, el sistema experimenta una compresión isoterma “1”, por el cuál el gas reduce su volumen a la mitad del valor inicial, pero manteniendo constante la temperatura T0. Una vez alcanzado el estado “B”, el sistema verifica una expansión isóbara “2” (a presión constante) hasta el estado “C”, para recuperar el volumen V0 del estado inicial. Finalmente, en un último proceso isócoro “3” (a volumen constante), se reduce la presión del sistema hasta el valor inicial P0, alcanzando de nuevo el estado “A”. El proceso cíclico se realiza de manera que pueda considerarse que el gas se encuentra, en todo momento, en equilibrio termodinámico.- De manera razonada y sin necesidad de realizar cálculos, qué puede decir acerca de las variaciones de energía interna en cada uno de los tres procesos parciales que constituyen el proceso cíclico descrito.
- Determine los valores de presión, volumen y temperatura del sistema en los estados “B” y “C”, en función de los valores iniciales.
- Para cada uno de los procesos parciales, indique de manera razonada el “sentido” en que se verifican las transferencias de calor y trabajo. Indique, asimismo, cómo es la transferencia neta de calor y trabajo en el proceso completo.
- Calcule el rendimiento del ciclo, definido como la relación entre el trabajo neto (en valor absoluto) transferido en el proceso cíclico, y la cantidad de calor absorbido Qin (es decir, sólo el que entra en el sistema).