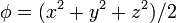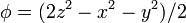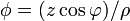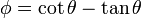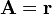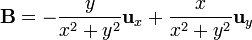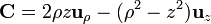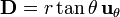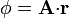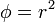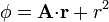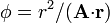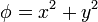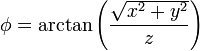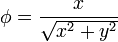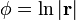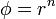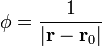Problemas de fundamentos matemáticos
De Laplace
(Diferencias entre revisiones)
| Línea 22: | Línea 22: | ||
# <math>\phi=\mathbf{A}{\cdot}\mathbf{r}+r^2\,</math> | # <math>\phi=\mathbf{A}{\cdot}\mathbf{r}+r^2\,</math> | ||
# <math>\phi= r^2/(\mathbf{A}{\cdot}\mathbf{r})</math> | # <math>\phi= r^2/(\mathbf{A}{\cdot}\mathbf{r})</math> | ||
| - | # <math>\phi = x^2 + y^2</math> | + | # <math>\phi = x^2 + y^2\,</math> |
# <math>\phi = \arctan\left(\displaystyle\frac{\sqrt{x^2+y^2}}{z}\right)</math> | # <math>\phi = \arctan\left(\displaystyle\frac{\sqrt{x^2+y^2}}{z}\right)</math> | ||
# <math>\phi= \frac{x}{\sqrt{x^2+y^2}}</math> | # <math>\phi= \frac{x}{\sqrt{x^2+y^2}}</math> | ||
donde <math>\mathbf{A}</math> es un vector constante y <math>\mathbf{r}</math> es el vector de posición. | donde <math>\mathbf{A}</math> es un vector constante y <math>\mathbf{r}</math> es el vector de posición. | ||
| + | |||
| + | ==[[Cálculo de gradientes]]== | ||
| + | Para los campos escalares | ||
| + | |||
| + | # <math>\phi = (x^2+y^2+z^2)/2\,</math> | ||
| + | # <math>\phi = (2z^2-x^2-y^2)/2\,</math> | ||
| + | |||
| + | calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas. | ||
| + | |||
| + | ==[[Regla de la cadena para gradientes]]== | ||
| + | Si <math>\phi = \phi(u)\,</math>, con <math>u = u(\mathbf{r})</math>, demuestre que | ||
| + | |||
| + | <center><math>\nabla \phi = \frac{\mathrm{d}\phi}{\mathrm{d}u} \nabla u</math></center> | ||
| + | |||
| + | Encuentre <math>\nabla \phi</math> si | ||
| + | |||
| + | # <math>\phi=\ln|\mathbf{r}|\,</math> | ||
| + | # <math>\phi =r^n\,</math> | ||
| + | # <math>\phi=\frac{1}{|\mathbf{r} -\mathbf{r}_0|}</math> | ||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
Revisión de 09:46 23 sep 2008
Contenido |
1 Campos escalares en diferentes sistemas
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2 Campos vectoriales en diferentes sistemas
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:
3 Trazado de superficies equiescalares
Describa las superficies equipotenciales de los siguientes campos escalares
donde  es un vector constante y
es un vector constante y  es el vector de posición.
es el vector de posición.
4 Cálculo de gradientes
Para los campos escalares
calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas.
5 Regla de la cadena para gradientes
Si 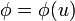 , con
, con 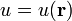 , demuestre que
, demuestre que
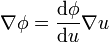
Encuentre 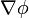 si
si