Cálculos de entropía (GIE)

De Laplace

(Diferencias entre revisiones)

Revisión de 10:01 17 mar 2012

Contenido

1 Transferencia de calor
2 Cambio de fase
3 Calentamiento de una sustancia pura
4 Inmersión en un baño térmico
5 Gas ideal
6 Mezcla de gases
7 Reacciones químicas

1 Transferencia de calor

El caso más simple de producción de entropía se da cuando tenemos calor que pasa de un cuerpo caliente a uno frío. Si tenemos dos focos a temperaturas $T 1$ y $T 2$ y una cierta cantidad de calor $Q$ pasa del 1 al 2, se produce una disminución de entropía en el primero

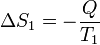
$\Delta S_1 = -\frac{Q}{T_1}$

y un aumento en el segundo

$\Delta S_2 = +\frac{Q}{T_2}$

resultando una variación neta en el universo

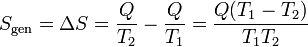
$S_\mathrm{gen}=\Delta S = \frac{Q}{T_2}-\frac{Q}{T_1}= \frac{Q(T_1-T_2)}{T_1T_2}$

Para que este proceso sea posible, debe ser $T 1 > T 2$ , como afirma el enunciado de Clausius.

Normalmente las temperaturas de los focos pueden estar cambiando en el tiempo (por ejemplo, un café que se va enfriando tiene una temperatura que se acerca exponencialmente a su valor final). En ese caso debemos considerar el ritmo al que se produce la entropía

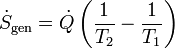
$\dot{S}_\mathrm{gen}=\dot{Q}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)$

midiéndose el ritmo de producción en el SI en (J/K)/s = W/K.

Como modelo de cómo ocurre esta producción de entropía podemos considerar la conducción de calor. Si los dos focos térmicos están separados por una lámina conductora del calor, para la que se verifica la ley de Fourier

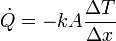
$\dot{Q}=-kA\frac{\Delta T}{\Delta x}$

estando uno de sus lados a una temperatura $T 1$ y el otro a temperatura $T 2$ . Aquí suponemos el sentido del flujo de calor del medio 1 al 2 y $Δ T = T 2 - T 1$ . En este caso el ritmo de producción de entropía

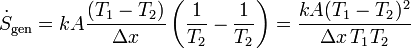
$\dot{S}_\mathrm{gen}= kA\frac{(T_1-T_2)}{\Delta x}\left(\frac{1}{T_2}-\frac{1}{T_2}\right) = \frac{kA(T_1-T_2)^2}{\Delta x\,T_1T_2}$

Por ejemplo, a través de una ventana cuyo exterior está a 15°C y cuyo interior a 22°C, siendo las dimensiones de la ventana 1.60×1.20 m² su espesor 5 mm y su conductividad térmica 0.96 W/m·K, el ritmo de producción de entropía es

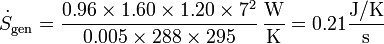
$\dot{S}_\mathrm{gen} = \frac{0.96\times 1.60\times 1.20\times 7^2}{0.005\times 288\times 295}\,\frac{\mathrm{W}}{\mathrm{K}} = 0.21\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}$

2 Cambio de fase

Un cambio de fase es un proceso aproximadamente isotermo, por lo que la variación de la entropía de una sustancia cuando experimenta un cambio de fase es simplemente

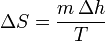
$\Delta S = \frac{m\,\Delta h}{T}$

siendo $Δ h$ la entalpía por unidad de masa del cambio de fase (de fusión o de vaporización, por ejemplo, para el agua).

Así, en el paso de hielo sólido a agua a 1 atm se produce un aumento de entropía por unidad de masa ( $s = S / m$ ):

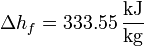
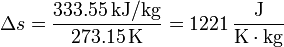
$\Delta h_f = 333.55\,\frac{\mathrm{kJ}}{\mathrm{kg}}$ $\Rightarrow$ $\Delta s = \frac{333.55\,\mathrm{kJ}/\mathrm{kg}}{273.15\,\mathrm{K}}=1221\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{kg}}$

y en el paso de agua a vapor de agua a 1 atm

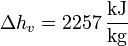
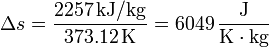
$\Delta h_v=2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}$ $\Rightarrow$ $\Delta s = \frac{2257\,\mathrm{kJ}/\mathrm{kg}}{373.12\,\mathrm{K}}=6049\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{kg}}$

Vemos que es mucho mayor el aumento en la ebullición que en la fusión. Esto está asociado con el gran aumento del desorden al pasar de líquido a gas.

3 Calentamiento de una sustancia pura

Cuando se tiene una sustancia pura, como el agua, que experimenta una variación de su temperatura, siendo la presión inicial y la final la misma, la variación de la entropía de la sustancia es, según la definición

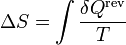
$\Delta S = \int \frac{\delta Q^\mathrm{rev}}{T}$

Como proceso reversible podemos imaginar uno en el que la temperatura de la sustancia va variando gradualmente por igual en todos sus puntos, siendo la presión siempre la misma. En este caso

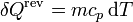
$\delta Q^\mathrm{rev} = mc_p\,\mathrm{d}T$

y la variación de entropía es

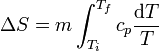
$\Delta S = m \int_{T_i}^{T_f}c_p\frac{\mathrm{d}T}{T}$

El calor específico es, en general, una función de la temperatura y debe ser tenido en cuenta a la hora de integrar. No obstante, si el rango de variación de la temperatura es pequeño, usualmente se puede aproximar $c p$ por una constante, su valor medio, y obtener la expresión

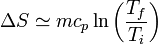
$\Delta S \simeq mc_p\ln\left(\frac{T_f}{T_i}\right)$

Combinado este resultado con el anterior, podemos trazar la gráfica de la entropía por unidad de masa, como función de la temperatura, para el agua desde el estado de hielo al de vapor, tomando como referencia el punto de fusión:

Problemas relacionados:
- Variación de entropía en el paso de hielo a vapor
- Inmersión de un bloque metálico en agua

4 Inmersión en un baño térmico

Un caso frecuente de cálculo de entropía es aquel en que se tiene una sustancia pura, a una temperatura $T 1$ y se sumerge en un baño a temperatura $T 2$ , manteniéndose constante la presión. La sustancia se enfría (o se calienta, según el caso) hasta adaptarse a la temperatura del baño.

La variación de la entropía de la sustancia (si el calor específico se supone constante) es, según el apartado anterior

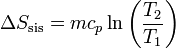
$\Delta S_\mathrm{sis}=mc_p\ln\left(\frac{T_2}{T_1}\right)$

La entropía del baño también cambia, pues absorbe calor a una temperatura constante. La cantidad de calor que se intercambia con el ambiente es

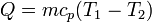
$Q = mc_p(T_1-T_2)\,$

Este calor sale del sistema y entra en el ambiente, por lo que la variación de entropía del baño es

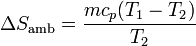
$\Delta S_\mathrm{amb}=\frac{mc_p(T_1-T_2)}{T_2}$

y la variación total de la entropía del universo será

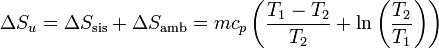
$\Delta S_u = \Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=mc_p\left(\frac{T_1-T_2}{T_2}+\ln\left(\frac{T_2}{T_1}\right)\right)$

Puede probarse de foma sencilla que, tanto si $T 1 > T 2$ como si $T 1 < T 2$ , esta variación es siempre positiva, esto es, el sistema siempre adquiere la temperatura del baño.

Problema relacionado: Comparación de dos variaciones de entropía

5 Gas ideal

Para un gas ideal podemos obtener una expresión válida para una presión y temperatura arbitrarias.

5.1 Expresión en función de T y V

Para un gas ideal puro, podemos calcular el incremento diferencial de entropía a partir de la definición

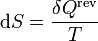
$\mathrm{d}S=\frac{\delta Q^\mathrm{rev}}{T}$

A su vez, el diferencial de calor reversible puede hallarse mediante el primer principio de la termodinámica

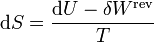
$\mathrm{d}S=\frac{\mathrm{d}U-\delta W^\mathrm{rev}}{T}$

Para un gas ideal sabemos que

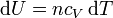
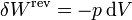
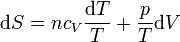
$\mathrm{d}U = nc_V\,\mathrm{d}T$ $\delta W^\mathrm{rev}=-p\,\mathrm{d}V$ $\Rightarrow$ $\mathrm{d}S=nc_V\frac{\mathrm{d}T}{T}+\frac{p}{T}\mathrm{d}V$

Sustituyendo la ecuación de estado del gas ideal $p V = n R T$ queda

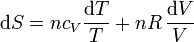
$\mathrm{d}S = nc_V\frac{\mathrm{d}T}{T}+nR\,\frac{\mathrm{d}V}{V}$

Si suponemos que la capacidad calorífica molar es independiente de la temperatura, podemos integrar esta ecuación para hallar el incremento entre dos estados

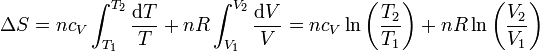
$\Delta S = nc_V\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}+nR\int_{V_1}^{V_2}\frac{\mathrm{d}V}{V}= nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right)$

5.2 Expresión en función de T y p

Si lo que tenemos es el cambio en la presión, en lugar del volumen, podemos hacer un cálculo análogo empleando la entalpía

$\mathrm{d}S=\frac{\delta Q_\mathrm{rev}}{T}=\frac{\mathrm{d}H-V\,\mathrm{d}p}{T}$

La entalpía se relaciona con la temperatura a través de la capacidad calorífica a presión constante

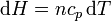
$\mathrm{d}H = nc_p\,\mathrm{d}T$

lo que lleva a la expresión para el incremento de entropía

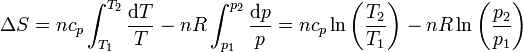
$\Delta S = nc_p\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}-nR\int_{p_1}^{p_2}\frac{\mathrm{d}p}{p}= nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)$

También se puede llegar a este resultado sustituyendo en la expresión de la entropía como función de T y V, el volumen como función de p y T, mediante la ecuación de los gases ideales. Tenemos que

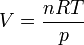
$V = \frac{nRT}{p}$

Sustituyendo en la expresión del apartado anterior

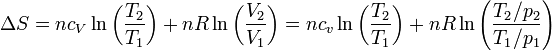
$\Delta S = nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right) = nc_v\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{T_2/p_2}{T_1/p_1}\right)$

Desarrollando el logaritmo

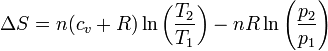
$\Delta S = n(c_v+R)\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)$

y aplicando la ley de Mayer

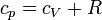
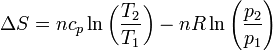
$c_p = c_V + R\,$ $\Rightarrow$ $\Delta S = nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)$

Como en el apartado anterior, este resultado se ha obtenido suponiendo que la capacidad calorífica no depende de la temperatura. Para variaciones grandes de ésta, es un efecto que se debe tener en cuenta y el resultado es más complicado.

Si uno de los dos estados es el estándar la entropía en cualesquiera otras condiciones será

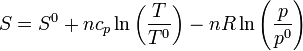
$S = S^0 + nc_p\ln\left(\frac{T}{T^0}\right)-nR\ln\left(\frac{p}{p^0}\right)$

5.3 En función de p y V

En la expresión anterior podemos sustituir la temperatura y obtener

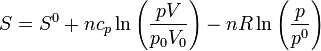
$S = S^0 + nc_p\ln\left(\frac{pV}{p_0V_0}\right)-nR\ln\left(\frac{p}{p^0}\right)$

y, aplicando las propiedades de los logaritmos

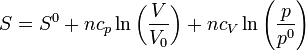
$S = S^0 + nc_p\ln\left(\frac{V}{V_0}\right)+nc_V\ln\left(\frac{p}{p^0}\right)$

Despejando, dividiendo por $n c V$ y hallando la exponencial:

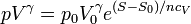
$pV^\gamma = p_0V_0^\gamma e^{(S-S_0)/nc_V}$

con $γ = c p / c V$ . Un proceso adiabático reversible es siempre isentrópico por lo que $p V γ$ es una constante en esta clase de procesos, como establece la ley de Poisson. Ahora además sabemos cuánto vale dicha constante.

6 Mezcla de gases

Supongamos que tenemos $n k$ moles de N gases, todos a la misma temperatura $T 0$ y presión $p 0$ , separados por tabiques. Si se retiran los tabiques y los gases se mezclan, se producirá un aumento de entropía, por tratarse de un proceso irreversible.

Si suponemos que los gases son ideales e inertes (esto es, que no reaccionan ni se ven afectados por el hecho de mezclarse), la entropía será la suma de las entropías individuales, como corresponde a una propiedad extensiva

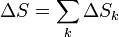
$\Delta S = \sum_k \Delta S_k\,$

A su vez, los incrementos de la entropía para cada gas serán

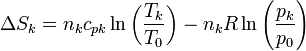
$\Delta S_k = n_k c_{pk}\ln\left(\frac{T_k}{T_0}\right)-n_kR\ln\left(\frac{p_{k}}{p_{0}}\right)$

Al mezclarse los gases la temperatura de cada gas es la misma antes y después de la mezcla. En cuanto a la presión, la presión final de la mezcla es la misma que la de cada gas al principio. Sin embargo, la presión final de cada gas no es la misma, sino que se reduce a la presión parcial

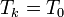
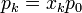
$T_k = T_0\,$ $p_k = x_kp_0\,$

ya que, por ser inertes, la variación de la entropía se calcula como si el resto de los gases no estuviera presente. Por tanto, para cada gas, es como si pasara de ocupar un espacio pequeño a uno más grande. Aquí $x k$ es la fracción molar

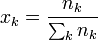
$x_k = \frac{n_k}{\sum_k n_k}$

Por tanto, la variación de la entropía para cada gas es

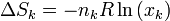
$\Delta S_k = -n_kR\ln\left(x_k\right)$

y la variación total

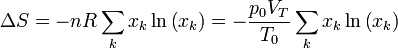
$\Delta S = -n R \sum_kx_k\ln\left(x_k\right)=-\frac{p_0V_T}{T_0}\sum_k x_k\ln\left(x_k\right)$

Esta variación es positiva, como corresponde a un proceso irreversible.

Supongamos, por ejemplo que la mezcla es de oxígeno y nitrógeno, ambos en la misma cantidad

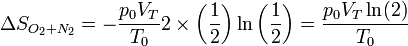
$\Delta S_{O_2+N_2} = -\frac{p_0V_T}{T_0}2\times\left(\frac{1}{2}\right)\ln\left(\frac{1}{2}\right)=\frac{p_0V_T\ln(2)}{T_0}$

El resultado anterior es independiente de qué gases sean los que se mezclan, pero, ¿qué ocurre si mezclamos oxígeno con más oxígeno? La fórmula seguiría siendo la misma. Sin embargo, si se tienen dos volúmenes del mismo gas a la misma presión y temperatura y se elimina la separación entre ellos, la situación antes de la mezcla y después, es exactamente la misma y por tanto el aumento de entropía es nulo. Hay aquí una discontinuidad que parece depender de que uno sepa qué está mezclando. Esta es la conocida como paradoja de Gibbs y su solución no es trivial.

Problema relacionado: Entropía de una mezcla de gases

7 Reacciones químicas

Cuando se analiza una reacción química lo que se suele hacer es

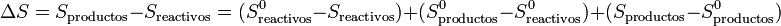
$\Delta S = S_\mathrm{productos}-S_\mathrm{reactivos}= (S^0_\mathrm{reactivos}-S_\mathrm{reactivos})+(S_\mathrm{productos}^0-S_\mathrm{reactivos}^0)+(S_\mathrm{productos}-S_\mathrm{productos}^0)$

siendo $S 0$ las entropías medidas y tabuladas en el estado estándar (normalmente a 100 kPa y 298 K). La segunda diferencia representa la variación de la entropía en la reacción en el estado estándar

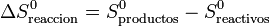
$\Delta S^0_\mathrm{reaccion}=S_\mathrm{productos}^0-S_\mathrm{reactivos}^0$

Lo que quiere decir esta descomposición en tres sumas es que, para estudiar una reacción a una cierta presión y temperatura, aprovechamos el que la entropía es una función de estado. En lugar de calcular la diferencia directamente a dicha $p$ y $T$ , lo que hacemos es imaginarnos que llevamos los reactivos, sin reaccionar, al estado estándar. Luego analizamos la reacción en el estado estándar, aprovechando los valores tabulados. Por último llevamos los productos a las condiciones originales.

@@ Línea 52: / Línea 52: @@
 Cuando se tiene una sustancia pura, como el agua, que experimenta una variación de su temperatura, siendo la presión inicial y la final la misma, la variación de la entropía de la sustancia es, según la definición
-<center><math>\Delta S = \int \frac{\delta Q_R}{T}</math></center>
+<center><math>\Delta S = \int \frac{\delta Q^\mathrm{rev}}{T}</math></center>
 Como proceso reversible podemos imaginar uno en el que la temperatura de la sustancia va variando gradualmente por igual en todos sus puntos, siendo la presión siempre la misma. En este caso
-<center><math>\delta Q_R = mc_p\,\mathrm{d}T</math></center>
+<center><math>\delta Q^\mathrm{rev} = mc_p\,\mathrm{d}T</math></center>
 y la variación de entropía es
@@ Línea 103: / Línea 103: @@
 Para un gas ideal puro, podemos calcular el incremento diferencial de entropía a partir de la definición
-<center><math>\mathrm{d}S=\frac{\delta Q_R}{T}</math></center>
+<center><math>\mathrm{d}S=\frac{\delta Q^\mathrm{rev}}{T}</math></center>
 A su vez, el diferencial de calor reversible puede hallarse mediante el primer principio de la termodinámica
-<center><math>\mathrm{d}S=\frac{\mathrm{d}U-\delta W_R}{T}</math></center>
+<center><math>\mathrm{d}S=\frac{\mathrm{d}U-\delta W^\mathrm{rev}}{T}</math></center>
 Para un gas ideal sabemos que
-<center><math>\mathrm{d}U = nc_V\,\mathrm{d}T</math>{{qquad}}{{qquad}}<math>\delta W_R=-p\,\mathrm{d}V</math>{{tose}}<math>\mathrm{d}S=nc_V\frac{\mathrm{d}T}{T}+\frac{p}{T}\mathrm{d}V</math></center>
+<center><math>\mathrm{d}U = nc_V\,\mathrm{d}T</math>{{qquad}}{{qquad}}<math>\delta W^\mathrm{rev}=-p\,\mathrm{d}V</math>{{tose}}<math>\mathrm{d}S=nc_V\frac{\mathrm{d}T}{T}+\frac{p}{T}\mathrm{d}V</math></center>
 Sustituyendo la ecuación de estado del gas ideal <math>pV=nRT</math> queda

Cálculos de entropía (GIE)

De Laplace

Revisión de 10:01 17 mar 2012

Contenido

1 Transferencia de calor

2 Cambio de fase

3 Calentamiento de una sustancia pura

4 Inmersión en un baño térmico

5 Gas ideal

5.1 Expresión en función de T y V

5.2 Expresión en función de T y p

5.3 En función de p y V

6 Mezcla de gases

7 Reacciones químicas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES