Problemas de materiales dieléctricos
De Laplace
| Línea 24: | Línea 24: | ||
# Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste? | # Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste? | ||
# Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica? | # Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica? | ||
| + | # Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como | ||
| + | |||
| + | <center><math>\mathbf{P} = \mathbf{P}_0 +\varepsilon\chi_e\mathbf{E}</math></center> | ||
| + | |||
| + | ===Esfera polarizada radialmente=== | ||
| + | Se tiene una esfera de radio <math>R</math>, centrada en el origen, compuesta de un material con una polarización radial | ||
| + | |||
| + | <center><math>\mathbf{P}=P_0\mathbf{u}_{r}</math></center> | ||
| + | |||
| + | # Calcule la distribución de cargas equivalente a esta polarización. | ||
| + | # Determine los campos <math>\mathbf{D}</math> y <math>\mathbf{E}</math> en todo el espacio. | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 17:50 20 jun 2008
Contenido |
1 Permitividad de un gas noble
El estudio de las propiedades dieléctricas de los gases puede servir para medir el tamaño de los átomos.
Para ello, suponga que se modela un átomo de número atómico Z como compuesto de una carga puntual Ze (el núcleo) y una nube esférica uniforme, con volumen τ (los electrones). Si a un átomo de este tipo se le aplica un campo externo uniforme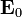 
, ¿cuánto vale el momento dipolar inducido en el átomo por la separación de los centros de carga?
Para un gas monoatómico (un gas noble) con una densidad de N átomos por unidad de volumen, ¿cuánto valdrá la susceptibilidad y la permitividad?
Experimentalmente se comprueba que el helio en condiciones normales tiene una permitividad relativa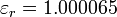 
, mientras que para el neón 
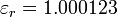, y para el argón 
. Según esto, ¿cuál es el tamaño de un átomo de cada uno de estos gases nobles?
2 Esfera polarizada uniformemente
Se tiene una esfera dieléctrica de radio R polarizada uniformemente con 
.
- Halle, por integración directa el potencial eléctrico en todos los puntos del espacio.
- ¿Cuáles son los valores de
, 
y 
dentro y fuera de la esfera?
- ¿Cuánto valen las densidades de carga equivalentes a la polarización?
3 Medio polarizado entre dos placas
Entre dos placas metálicas planas y paralelas, de sección S y separadas una distancia a, se encuentra un dieléctrico que presenta polarización remanente, de forma que en él
siendo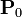 
un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
- Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste?
- Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica?
- Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como
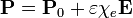
4 Esfera polarizada radialmente
Se tiene una esfera de radio R, centrada en el origen, compuesta de un material con una polarización radial
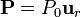
- Calcule la distribución de cargas equivalente a esta polarización.
- Determine los campos y en todo el espacio.
