Ecuaciones de Maxwell y teorema de Poynting
De Laplace
(Diferencias entre revisiones)
(→Problemas) |
(→Problemas) |
||
| Línea 11: | Línea 11: | ||
# El espacio entre dos placas circulares perfectamente conductoras, planas y paralelas, se encuentra lleno de un material óhmico, de permitividad <math>\varepsilon</math>, conductividad <math>\sigma</math>, y permeabilidad magnética <math>\mu_0</math>. El radio de las placas es <math>b</math>, y la distancia entre ellas es <math>a</math> ($a\ll b$). La placa superior está permanentemente a tierra, mientras que el centro de la inferior se encuentra a una tensión <math>V(t)</math>. ([[Teorema de Poynting para un condensador|Más]]) | # El espacio entre dos placas circulares perfectamente conductoras, planas y paralelas, se encuentra lleno de un material óhmico, de permitividad <math>\varepsilon</math>, conductividad <math>\sigma</math>, y permeabilidad magnética <math>\mu_0</math>. El radio de las placas es <math>b</math>, y la distancia entre ellas es <math>a</math> ($a\ll b$). La placa superior está permanentemente a tierra, mientras que el centro de la inferior se encuentra a una tensión <math>V(t)</math>. ([[Teorema de Poynting para un condensador|Más]]) | ||
# Un cable coaxial ideal está formado por un cilindro interior, de radio <math>a</math>, perfectamente conductor, y una superficie cilíndrica exterior, de radio <math>b</math>, también perfectamente conductora. Los cilindros se extienden indefinidamente a lo largo de su eje... ([[Teorema de Poynting en un cable coaxial|más]]) | # Un cable coaxial ideal está formado por un cilindro interior, de radio <math>a</math>, perfectamente conductor, y una superficie cilíndrica exterior, de radio <math>b</math>, también perfectamente conductora. Los cilindros se extienden indefinidamente a lo largo de su eje... ([[Teorema de Poynting en un cable coaxial|más]]) | ||
| - | # Los campos eléctrico y magnético en el interior de un tubo metálico, de sección cuadrada (que se extiende entre <math>-a<x<a</math> y <math>-a<y<a</math>, e indefinidamente a lo largo del eje $z$) vienen dado por las expresiones... ([[Cálculo de fuentes del campo electromagnético|más]]) | + | # Los campos eléctrico y magnético en el interior de un tubo metálico, de sección cuadrada (que se extiende entre <math>-a<x<a</math> y <math>-a<y<a</math>, e indefinidamente a lo largo del eje $z$) vienen dado por las expresiones... ([[Cálculo de fuentes del campo electromagnético|más]]) |
| + | |||
[[Categoría:Ecuaciones de Maxwell]] | [[Categoría:Ecuaciones de Maxwell]] | ||
[[Categoría:Campos Electromagnéticos]] | [[Categoría:Campos Electromagnéticos]] | ||
Revisión de 10:36 23 may 2008
Contenido |
1 Introducción
2 Ecuaciones de Maxwell
3 La fuerza de Lorentz
4 Energía en un campo electromagnético. Teorema de Poynting
5 Expresión de las ecuaciones de Maxwell en función de los potenciales
6 Problemas
Artículo principal: Problemas de Ecuaciones de Maxwell
- Se tiene un condensador formado por dos placas circulares planas y paralelas, de radio b y separadas una distancia a (
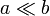); entre ellas hay vacío. Entre los centros de las placas se establece una tensión V0cosωt... (más)
- Una nube esférica de carga (compuesta de una distribución de cargas puntuales flotando en el vacío) se encuentra en expansión, creciendo el radio de la esfera como R(t) = R0 + vt. La carga total de la nube, Q0, se encuentra distribuida en todo momento de forma uniforme en el volumen de la esfera.... (más)
- El espacio entre dos placas circulares perfectamente conductoras, planas y paralelas, se encuentra lleno de un material óhmico, de permitividad
, conductividad σ, y permeabilidad magnética μ0. El radio de las placas es b, y la distancia entre ellas es a ($a\ll b$). La placa superior está permanentemente a tierra, mientras que el centro de la inferior se encuentra a una tensión V(t). (Más)
- Un cable coaxial ideal está formado por un cilindro interior, de radio a, perfectamente conductor, y una superficie cilíndrica exterior, de radio b, también perfectamente conductora. Los cilindros se extienden indefinidamente a lo largo de su eje... (más)
- Los campos eléctrico y magnético en el interior de un tubo metálico, de sección cuadrada (que se extiende entre − a < x < a y − a < y < a, e indefinidamente a lo largo del eje $z$) vienen dado por las expresiones... (más)
