Segunda Prueba de Control 2013/14 (F1 G.I.A.)
De Laplace
| Línea 5: | Línea 5: | ||
[[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] | [[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] | ||
| - | |||
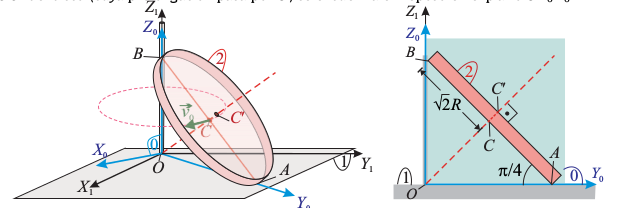
Un disco de radio <math>\sqrt{2}R </math> y espesor no despreciable (sólido "2") se mueve respecto de un plano fijo <math>\Pi_1\equiv OX_1Y_1 </math> (sólido "1"). En cada instante, un punto del perímetro de la base inferior del disco está en contacto con el plano <math>\Pi_1 </math>, mientras que el diametralmente opuesto, se apoya sobre el eje fijo <math>OZ_1 </math>. En todo momento, las bases del disco forman un ángulo <math>\pi/4 </math> con el plano <math>\Pi_1 </math>. El movimiento del disco es tal que rueda sin deslizar sobre dicho plano, en el punto de contacto <math>A </math>. Además, el centro <math>C </math> de la base | Un disco de radio <math>\sqrt{2}R </math> y espesor no despreciable (sólido "2") se mueve respecto de un plano fijo <math>\Pi_1\equiv OX_1Y_1 </math> (sólido "1"). En cada instante, un punto del perímetro de la base inferior del disco está en contacto con el plano <math>\Pi_1 </math>, mientras que el diametralmente opuesto, se apoya sobre el eje fijo <math>OZ_1 </math>. En todo momento, las bases del disco forman un ángulo <math>\pi/4 </math> con el plano <math>\Pi_1 </math>. El movimiento del disco es tal que rueda sin deslizar sobre dicho plano, en el punto de contacto <math>A </math>. Además, el centro <math>C </math> de la base | ||
inferior realiza un movimiento circular de radio <math>R </math> en torno al eje <math>OZ_1 </math>, en sentido horario y con velocidad de módulo constante <math>v_0 </math>. Para analizar el movimiento, se sugiere utilizar un sólido ("0") consistente en un sistema de referencia <math>OX_0Y_0Z_0 </math> tal que <math>OZ_0 = OZ_1 </math> en todo instante y que se mueve de manera que el eje <math>CC' </math> del disco (cuya prolongación pasa por <math>O </math>) se encuentra en reposo en el plano <math>OY_0Z_0 </math>. | inferior realiza un movimiento circular de radio <math>R </math> en torno al eje <math>OZ_1 </math>, en sentido horario y con velocidad de módulo constante <math>v_0 </math>. Para analizar el movimiento, se sugiere utilizar un sólido ("0") consistente en un sistema de referencia <math>OX_0Y_0Z_0 </math> tal que <math>OZ_0 = OZ_1 </math> en todo instante y que se mueve de manera que el eje <math>CC' </math> del disco (cuya prolongación pasa por <math>O </math>) se encuentra en reposo en el plano <math>OY_0Z_0 </math>. | ||
#Trace los ejes de rotación de los movimientos {01}, {20} y {21} en el instante representado e identifique los tipos de movimiento. | #Trace los ejes de rotación de los movimientos {01}, {20} y {21} en el instante representado e identifique los tipos de movimiento. | ||
#Encuentre la reducción cinemática y su derivada para el movimiento {21}. | #Encuentre la reducción cinemática y su derivada para el movimiento {21}. | ||
| + | [[Imagen:F1_GIA_SPC_2013_disco_rotando_barra_vertical_enunciado.png|center]] | ||
Revisión de 19:49 7 ene 2015
Satélite girando alrededor de la Tierra
Disco rotando alrededor de barra vertical
Un disco de radio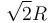 
y espesor no despreciable (sólido "2") se mueve respecto de un plano fijo 
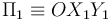(sólido "1"). En cada instante, un punto del perímetro de la base inferior del disco está en contacto con el plano Π1, mientras que el diametralmente opuesto, se apoya sobre el eje fijo OZ1. En todo momento, las bases del disco forman un ángulo π / 4 con el plano Π1. El movimiento del disco es tal que rueda sin deslizar sobre dicho plano, en el punto de contacto A. Además, el centro C de la base
inferior realiza un movimiento circular de radio R en torno al eje OZ1, en sentido horario y con velocidad de módulo constante v0. Para analizar el movimiento, se sugiere utilizar un sólido ("0") consistente en un sistema de referencia OX0Y0Z0 tal que OZ0 = OZ1 en todo instante y que se mueve de manera que el eje CC' del disco (cuya prolongación pasa por O) se encuentra en reposo en el plano OY0Z0.
- Trace los ejes de rotación de los movimientos {01}, {20} y {21} en el instante representado e identifique los tipos de movimiento.
- Encuentre la reducción cinemática y su derivada para el movimiento {21}.
