Calor y calorimetría

De Laplace

(Diferencias entre revisiones)

Revisión de 20:18 1 abr 2014

Contenido

1 Definición
2 Concepto de calor
3 Unidades y signos
4 Flujo de calor
5 Calor por unidad de masa
6 Calor e incremento de temperatura
- 6.1 Capacidad calorífica y calor específico
- 6.2 Capacidad calorífica molar
7 Calor y cambios de fase
8 Calor y equilibrio térmico
9 Baños térmicos
10 Paredes y procesos adiabáticos
11 Transferencia de calor
12 Dependencia del camino

1 Definición

Sección 2-3 de Çengel & Boles

Una posible definición de calor en termodinámica es la siguiente:

“El calor es la transferencia de energía a través de la frontera de un sistema debida a una diferencia de temperaturas”

De esta definición, cabe destacar varios aspectos que se detallan en las secciones siguientes y en otros artículos:

El calor, como el trabajo, es una transferencia de energía, un paso de energía de un sitio a otro, no algo que se tiene o se almacena. La frase “hace mucho calor” no es correcta en termodinámica.
El calor, como el trabajo, habla de lo que pasa en la frontera del sistema, no en su interior. Se debe a la interacción del sistema con su entorno.
El calor, a diferencia del trabajo, está asociado a la diferencia de temperatura, que es una medida de la agitación de los átomos y moléculas. Por tanto, se debe a la transferencia de energía a través de fenómenos microscópicos (el trabajo se refiere a los macroscópicos).

2 Concepto de calor

A diferencia del trabajo, el calor carece de analogía en mecánica, sino que es un concepto nuevo.

La experiencia nos dice que si colocamos un sistema en un cierto ambiente, el sistema evoluciona. Si colocamos un bloque de hielo al sol, sabemos que se funde. Si ponemos un termómetro de mercurio en la axila de una persona febril, el mercurio se dilata, y si es uno digital, se produce una corriente eléctrica en su interior.

Todos estos cambios se producen sin que haya trabajo asociado, simplemente por contacto. Deducimos entonces que “algo” ha pasado del entorno al sistema y a ese algo lo denominamos “calor”.

Los efectos del calor son varios:

Cambio en la temperatura del sistema
Cambio de fase del sistema
Realización de trabajo

la realización de trabajo como consecuencia de la transferencia de calor se explica al estudiar el primer principio de la termodinámica y el funcionamiento de las máquinas térmicas. En este artículo describiremos los dos primeros efectos.

3 Unidades y signos

El calor es una transferencia de energía y se mide en las mismas unidades que ésta. En el SI, la unidad del calor es el julio (J).

Por razones históricas, se usa también la caloría (cal), definida hoy día como

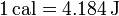
$1\,\mathrm{cal} = 4.184\,\mathrm{J}$

Sin embargo, debido a la existencia de diferentes definiciones de caloría, es preferible no usarla en absoluto. También se usa en medicina, biología y dietética la “caloría grande” (Cal), que en realidad es una kilocaloría ( = 4184 J).

En máquinas térmicas y refrigeradores se usa una unidad británica, la BTU, equivalente a 1055.056 J.

Como criterio para asignar signos al calor se sigue el principio de que:

Si el calor entra en el sistema se considera positivo.
Si el calor sale del sistema, es negativo.

Alternativamente, si presuponemos un sentido en el que está fluyendo el calor (calor que entra desde un foco a alta temperatura, o es desechado al ambiente frío), podemos definir

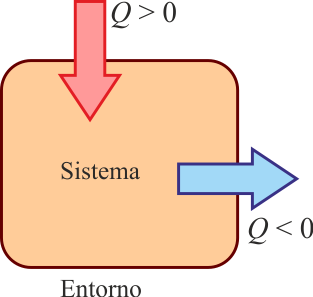
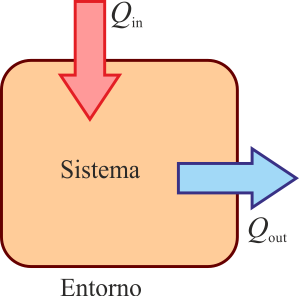
$Q in$ para el calor que entra en el sistema
$Q out$ para el calor que sale del sistema

siendo el calor neto intercambiado

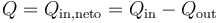
$Q=Q_\mathrm{in,neto}=Q_\mathrm{in}-Q_\mathrm{out}\,$

Tanto $Q in$ como $Q out$ pueden resultar negativos. Ello significa que el calor va en el sentido contrario al que habíamos supuesto.

4 Flujo de calor

En muchas ocasiones, no se está tan interesado en cuánto vale el calor total absorbido, sino cuánto calor entra en el sistema en la unidad de tiempo. Por ello se define el flujo de calor como

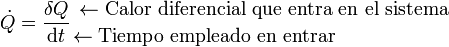
$\dot{Q}=\frac{\delta Q}{\mathrm{d}t}{{\leftarrow \mbox{Calor diferencial que entra en el sistema}}\atop {\leftarrow \mbox{Tiempo empleado en entrar}\qquad\qquad\qquad\,}}$

(¡Ojo al punto sobre la Q!). Se mide en el SI, como la potencia, en vatios ( $W$ ).

El criterio de signos para el flujo de calor es el mismo que para el calor. Si está entrando calor en el sistema el flujo es positivo; si sale de él, es negativo.

Del mismo modo, podemos definir un flujo de calor hacia dentro o hacia afuera del sistema

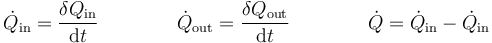
$\dot{Q}_\mathrm{in}=\frac{\delta Q_\mathrm{in}}{\mathrm{d}t}\qquad\qquad\dot{Q}_\mathrm{out}=\frac{\delta Q_\mathrm{out}}{\mathrm{d}t}\qquad\qquad\dot{Q}=\dot{Q}_\mathrm{in}-\dot{Q}_\mathrm{in}$

5 Calor por unidad de masa

El calor que entra en un sistema es una propiedad extensiva. En el caso de una sustancia pura o una mezcla de gases, el efecto del calor depende de la cantidad de materia que haya. Si lo que interesa es la cantidad de calor que entra o sale relativa a la masa, conviene usar el calor por unidad de masa

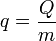
$q = \frac{Q}{m}$

El calor por unidad de masa se mide en el SI en J/kg.

6 Calor e incremento de temperatura

(Sección 4-3 de Çengel & Boles, "Calores específicos")

El primer efecto observable de la transferencia de calor a un sistema es el incremento de su temperatura. Hay que destacar que no siempre que entra calor en un sistema se produce un aumento de temperatura, depende de si también hay cambios de fase o se está realizando trabajo.

Suponiendo que la temperatura sí varía, si la cantidad de calor transferida es pequeña, la variación de temperatura es proporcional a ella, lo que se expresa matemáticamente

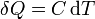
$\delta Q = C\,\mathrm{d}T$

siendo $C$ una propiedad del sistema denominada capacidad calorífica. De la definición se tiene que la capacidad calorífica se mide en el SI en J/K.

El calor diferencial es una diferencial inexacta (por eso expresa con el símbolo “δ”), lo que quiere decir que depende del proceso. Una misma cantidad de calor transferida a un sistema puede producir diferentes incrementos de temperatura, dependiendo de cómo se realice.

Dos casos particulares son importantes. Cuando se transfiere de manera cuasiestática calor a un sistema gaseoso

si ocurre en un recipiente rígido, tenemos que el volumen es constante y

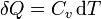
$\delta Q = C_v\,\mathrm{d}T$

siendo

C v

la capacidad calorífica a volumen constante.

Si el calor se comunica en un sistema abierto a la atmósfera, o con paredes que pueden moverse libremente, entonces la presión del sistema permanece constante (en un proceso cuasiestático, el sistema estará siempre en un estado de equilibrio mecánico con el exterior) y

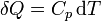
$\delta Q = C_p\,\mathrm{d}T$

siendo

C p

la capacidad calorífica a presión constante.

Cuando se estudia el efecto del calor en el calentamiento de un sólido o un líquido se presupone que ocurre en un sistema abierto y que por tanto, aunque no se indique se trata de una capacidad calorífica a presión constante.

Las capacidades caloríficas dependen de la temperatura, ya que no cuesta lo mismo elevar la temperatura de agua de 10°C a 11°C (4.193 kJ/kg) que lo que cuesta pasar de 95°C a 96°C (4.213 kJ/kg). Por ello, si queremos realizar un aumento grande de temperatura, es necesario sumar los calores diferenciales.

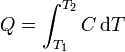
$Q = \int_{T_1}^{T_2} C\,\mathrm{d}T$

Si, como ocurre a menudo, la capacidad calorífica es aproximadamente constante en un rango de temperaturas, puede extraerse de la integral y escribirse

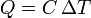
$Q = C\,\Delta T$

Cuando la capacidad calorífica es constante, podemos representar gráficamente la relación entre calor absorbido y aumento de temperatura mediante una línea recta. Despejando tenemos

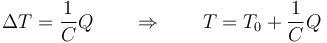
$\Delta T = \frac{1}{C}Q\qquad\Rightarrow\qquad T = T_0+\frac{1}{C}Q$

El que la capacidad vaya en el denominador quiere decir que cuanto mayor es la capacidad calorífgica, menor es la variación de temperatura para un valor dado del calor.

Cuando la capacidad calorífica no es constante, en lugar de una recta tendremos una curva.

6.1 Capacidad calorífica y calor específico

La Capacidad calorífica es una propiedad del sistema en su conjunto y depende de las propiedades de todas las partes del sistema. Además, como se ha indicado, no tiene el mismo valor para un proceso a presión constante que para uno a volumen constante.

La unidad de la capacidad calorífica es la de una energía dividida por una temperatura, en el SI se mide en J/K (aunque aun existen tablas donde aparece en cal/°C).

En el caso de una sustancia pura (agua, o un gas ideal, o incluso una mezcla de gases como el aire), la capacidad calorífica es una propiedad extensiva, proporcional a la cantidad de sustancia.

A partir de ella se define una propiedad específica: la capacidad calorífica por unidad de masa, más conocida como calor específico

$c = \frac{C}{m}$

En términos del calor específico, la cantidad de calor necesaria para producir un aumento diferencial de temperatura y uno finito

$\delta Q = mc\,\mathrm{d}T\qquad\qquad Q = \int_{T_1}^{T_2}mc\,\mathrm{d}T\simeq mc\,\Delta T$

El calor específico tiene unidades en el SI de J/(kg·K). Su valor, como el de $C$ es dependiente de la temperatura, y tiene un valor diferente según sea un proceso a volumen constante ( $c v$ ) o a presión constante ( $c p$ ). Para sólidos y líquidos se suele tabular su valor a presión constante a la presión atmosférica y a una temperatura dada.

Así, su valor para algunas sustancias habituales es

Sustancia	$c p$ (kJ/kg·K)	Sustancia	$c p$ (kJ/kg·K)	Sustancia	$c p$ (kJ/kg·K)
Aire seco	1.012	Agua (20°C)	4.18	Cemento ligero	0.96
Cobre	0.385	Etanol (40°C)	0.65	Hielo (0°C)	2.09
Hierro (20°C)	0.46	Madera	2-3	Vapor de agua (100°C)	2.08

En la red pueden encontrase más valores para sólidos, líquidos y gases.

En el caso del agua su valor comienza por 4.204 kJ/(kg·K) a 0°C, baja hasta 4.178 a 35°C y vuelve a aumentar hasta 4.219 a 100°C. A temperatura ambiente, un valor de 4.18, con solo dos cifras decimales, suele ser más que suficiente.

Así para calentar 1kg de agua desde 0°C a 100°C, usando el valor anterior se necesitan

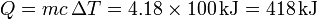
$Q = mc\,\Delta T = 4.18\times 100\,\mathrm{kJ} = 418\,\mathrm{kJ}$

Un valor más exacto, usando la tabla de la referencia anterior y considerando incrementos de 5°C en 5°C nos da un calor de 440 kJ. El error, aunque apreciable, es de solo el 5%. Este error se reduce aun más si consideramos incrementos menores de temperatura.

6.2 Capacidad calorífica molar

(Çengel & Boles: sección 4-4)

En el caso de un gas, en lugar de la capacidad específica por unidad de masa se suele usar la capacidad calorífica molar, denotada también con c minúscula

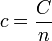
$c = \frac{C}{n}$

La capacidad calorífica molar se mide en J/(K·mol). Por ello, son sus unidades (y las expresiones en que aparece) las que permiten distinguirla del calor específico.

Como la capacidad calorífica y el calor específico, la capacidad calorífica molar se mide en dos variedades: a volumen constante ( $c v$ ) y a presión constante ( $c p$ ). Así, en procesos cuasiestáticos el calor necesario para producir un aumento diferencial de temperatura es

$\delta Q = nc_v\,\mathrm{d}T\qquad (V\ \mathrm{cte})\qquad\qquad \delta Q = nc_p\,\mathrm{d}T\qquad (p\ \mathrm{cte})$

Las unidades de $c p$ y $c v$ son las mismas que las de $R$ la constante de los gases ideales. Por ello, interesa saber no sólo cuanto valen en sentido absoluto, sino también relativamente a $R$ . Cuando se hace esto para una serie de gases habituales se obtiene la siguiente tabla

Gas	$c v$ J/(K·mol)	$c p$ J/(K·mol)	$c v / R$	$c p / R$	$γ = c p / c v$
He	12.5	20.8	1.50	2.50	1.67
Ne	12.5	20.8	1.50	2.50	1.67
Ar	12.5	20.8	1.50	2.50	1.67
H₂	20.18	28.82	2.42	3.47	1.43
N₂	20.8	29.12	2.50	3.50	1.40
O₂	21.1	29.38	2.54	3.54	1.39
CO₂	28.46	36.94	3.42	4.44	1.30
Metano (CH₄)	27.3	35.7	3.28	4.29	1.31
Vapor de agua	28.03	37.47	3.37	4.50	1.34

De esta tabla podemos obtener algunas conclusiones:

Para casi todos estos gases se cumple

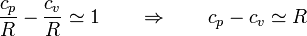
$\frac{c_p}{R}-\frac{c_v}{R}\simeq 1\qquad\Rightarrow\qquad c_p-c_v\simeq R$

esta propiedad se conoce como ley de Mayer.

Para los gases nobles (monoatómicos) se verifica casi exactamente

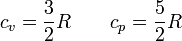
$c_v=\frac{3}{2}R\qquad c_p = \frac{5}{2}R$

Para los gases diatómicos (N₂, H₂, O₂) se cumple, pero con menor aproximación

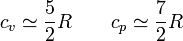
$c_v\simeq\frac{5}{2}R\qquad c_p \simeq \frac{7}{2}R$

Para los gases de más átomos (agua o CO₂, por ejemplo) no existe una fórmula sencilla para los valores de $c p$ y $c v$ .

En el caso del aire, al tratarse de una mezcla de gases y no de una sustancia pura, hay que tener cuidado al definir el concepto molar. Puede medirse experimentalmente el valor de los calores específicos (por unidad de masa) y luego considerar el gas como una sustancia con peso molecular el medio de sus componentes

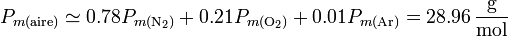
$P_{m\mathrm{(aire)}} \simeq 0.78P_{m\mathrm{(N_2)}}+0.21P_{m\mathrm{(O_2)}}+0.01P_{m\mathrm{(Ar)}} = 28.96\,\frac{\mathrm{g}}{\mathrm{mol}}$

Con esta precisión queda

Gas	$c v$ J/(K·mol)	$c p$ J/(K·mol)	$c v / R$	$c p / R$	$γ = c p / c v$
Aire	20.8	29.2	2.501	3.52	1.41

Vemos que, a estos efectos, el aire puede ser considerado como un gas diatómico.

La última columna de la tabla es la proporción entre capacidades caloríficas

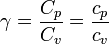
$\gamma = \frac{C_p}{C_v} = \frac{c_p}{c_v}$

Teniendo en cuenta que aproximadamente

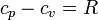
$c_p-c_v = R\,$

las dos capacidades caloríficas molares pueden escribirse en la forma

$c_v = \frac{R}{\gamma-1}\qquad\qquad c_p = \frac{\gamma R}{\gamma-1}$

Según estos datos, si tenemos inicialmente 0.1 m³ de aire a 300K y 100 kPa y queremos calentarlo hasta 600K manteniendo constante su volumen debemos introducir un calor

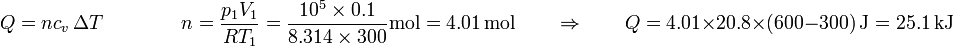
$Q = nc_v\,\Delta T\qquad\qquad n = \frac{p_1V_1}{RT_1}= \frac{10^5\times 0.1}{8.314\times 300}\mathrm{mol} = 4.01\,\mathrm{mol}\qquad\Rightarrow\qquad Q = 4.01\times 20.8\times(600-300)\,\mathrm{J}=25.1\,\mathrm{kJ}$

mientras que si lo que mantenemos constante es la presión

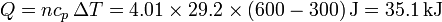
$Q = nc_p\,\Delta T = 4.01\times 29.2\times(600-300)\,\mathrm{J}=35.1\,\mathrm{kJ}$

En general se necesita más calor para realizar un calentamiento a presión constante que uno a volumen constante.

7 Calor y cambios de fase

Cuando se tiene un bloque de hielo a una temperatura de, por ejemplo, -10°C y se le comunica gradualmente calor, se aprecia que su temperatura va aumentando. Sin embargo, al llegar a la temperatura de 0°C, se detiene el incremento de temperatura. Durante un rato, aunque se añade calor, la temperatura del sistema permanece constante. En su lugar, lo que está ocurriendo es que el hielo a 0°C se va fundiendo transformándose en agua líquida, también a 0°C.

Una vez que todo el hielo se ha transformado en agua, se reanuda el aumento de temperatura, ahora con la capacidad calorífica del agua. Continúa el ascenso hasta que se llega a los 100°C, momento en que de nuevo se detiene el aumento, mientras el agua se transforma de manera turbulenta en vapor de agua, también a 100°C. Sólo cuando todo el agua se ha convertido en vapor de agua continúa el ascenso de temperatura, ahora con la capacidad calorífica del vapor de agua.

A la inversa ocurre si comenzamos con vapor y vamos extrayendo calor gradualmente. La temperatura va descendiendo, pero el descenso se interrumpe mientras el vapor se licúa y mientras el agua se congela.

Concluimos entonces que un segundo efecto del calor es el cambio de fase. A la temperatura del punto de fusión o de ebullición, el sistema absorbe o cede una cantidad de calor que es proporcional a la masa de sustancia que cambia de fase

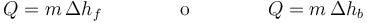
$Q = m\,\Delta h_f\qquad\qquad \mbox{o}\qquad\qquad Q = m\,\Delta h_b$

donde $Δ h f$ es la entalpía de fusíón y $Δ h b$ la entalpía de vaporización (o ebullición). Estas entalpía también se llaman “calores latentes”, aunque este nombre se desaconseja.

Hay que destacar que el valor de estas entalpías y la temperatura a la que se produce el cambio de fase son funciones de la presión. Cuando se dice “el agua se congela a 0°C” se entiende que es “a 101325 Pa de presión”, aunque no se diga. Lo mismo ocurre con la ebullición, que solo a esa presión se produce a 100°C (o siendo extremadamente precisos a 99.97°C). Si colocámos agua en un recipiente con un émbolo sobre el que situamos pesas de forma que la presión sea de 500 kPa, entonces la ebullición se produce a 151.8°C. También el valor de la entalpía de fusión y de ebullición es dependiente de la presión existente.

Asimismo, para los valores que aparecen en las tablas, se presupone que la ebullición se produce a presión constante, no a volumen constante, es decir, que al transformarse el líquido en vapor, éste se expande.

Así, por ejemplo, para el caso del agua tenemos

$\Delta h_f = 334\,\frac{\mathrm{kJ}}{\mathrm{kg}}\qquad\qquad \Delta h_b = 2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}$

Si deseamos hallar el calor necesario para llevar una masa de 1 kg de hielo desde -10°C al estado de vapor de agua a 315°C a la presión atmosférica, habrá que considerar tres valores para los incrementos de temperatura y dos para los cambios de fase, resultando una tabla como la siguiente

Paso	$Q$ (kJ)	Fracción del calor total (%)
Hielo a 0°C	21.2	0.7
Fusión	334	10.9%
Agua a 100°C	418	13.7%
Ebullición	2257	73.7%
Vapor a 115°C	31.4	1.0%
Total	3061.4	100

Vemos que la mayor parte del calor es necesario para pasar de la fase líquida a la gaseosa. En este cambio de fase es necesario romper los enlaces entre las moléculas de agua, lo cual requiere mucha más energía que un simple aumento de la agitación térmica.

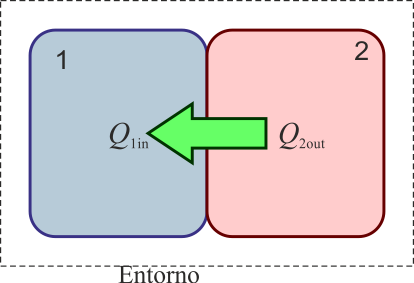
8 Calor y equilibrio térmico

Cuando se ponen en contacto dos sistemas (“1” y “2”) a diferente temperatura (por ejemplo, $T 2 > T 1$ ) se produce, de acuerdo con el segundo principio de la termodinámica, un flujo de calor desde el de más temperatura al de menos hasta que ambas temperaturas se igualan.

Si consideramos un sistema formado por las dos partes en contacto (sistema conjunto que no estará en equilibrio, por no estar todo él a la misma temperatura), entonces si el sistema está aislado térmicamente del exterior (por paredes adiabáticas)

$Q = 0\,$

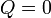
Por ser una propiedad extensiva el calor total es la suma de lo que va a cada parte

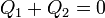
$Q_1 + Q_2 = 0\,$

que nos dice que todo el calor que sale de uno de los subsistemas va a parar al otro, sin desaparecer por el camino

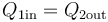
$Q_{1\mathrm{in}}=Q_{2\mathrm{out}}\,$

El resultado es una temperatura intermedia entre las iniciales de ambas partes. La temperatura final puede coincidir con el punto de fusión o el de ebullición si en uno de los sistemas ocurre un cambio de fase parcial. Si no ocurre, la temperatura final es una media ponderada de las dos iniciales

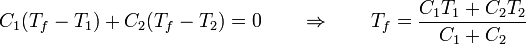
$C_1(T_f-T_1) +C_2(T_f-T_2) = 0\qquad\Rightarrow\qquad T_f = \frac{C_1 T_1+C_2T_2}{C_1+C_2}$

Gráficamente, sería lo siguiente: Tenemos inicialmente dos subsistemas a temperaturas diferentes, el calor que entra en el 1 sale del 2. Esto se ve como una recta creciente, para la temperatura del medio 1 y una decreciente para la del medio 2. Inicialmente cada parte tiene una temperatura distinta. El equilibrio se alcanza cuando las rectas se cortan. El valor del calor en ese punto es el que sale de una parte y entra en la otra.

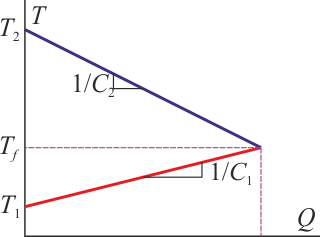
Si sí hay cambio de fase, es preciso analizar si el calor que sale de uno de los sistemas es suficiente para producir un cambio de fase de toda la sustancia o de solo una parte de ella. Por ejemplo, si ponemos en contacto 1 kg de hielo a 0°C con 1 kg de agua a 10°C, del agua solo salen 41.8 kJ, cuando se necesitan 334 kJ para fundir todo el hielo. Por ello, solo se funden 41.8/334 = 0.125 kg y el resultado final son 875 g de hielo y 1125 g de agua, ambos a 0°C.

En el caso particular de que se pongan en contacto dos cantidades de la misma sustancia (por ejemplo, que se vierta agua caliente en un baño de agua fría), la temperatura final se puede poner en función de las masas respectivas (suponiendo calores específicos independientes de la temperatura)

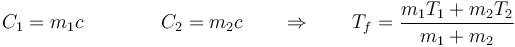
$C_1 = m_1c\qquad\qquad C_2 = m_2c\qquad\Rightarrow\qquad T_f = \frac{m_1T_1+m_2T_2}{m_1+m_2}$

9 Baños térmicos

Si se ponen en contacto dos subsistemas de capacidades caloríficas $C 0$ y $C 1$ , y no hay trasferencias de calor adicionales, según hemos visto la temperatura final del sistema es

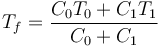
$T_f = \frac{C_0 T_0+C_1T_1}{C_0+C_1}$

Supongamos ahora que una de las dos capacidades es mucho mayor que la otra, 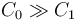$C_0\gg C_1$ . Por ejemplo, si sumergimos un vaso de agua caliente en una piscina fría. En ese caso

$T_f \simeq \frac{C_0T_0}{C_0}=T_0$

es decir, la temperatura final es aproximadamente la del de capacidad mayor. En el ejemplo del vaso de agua en la piscina, la temperatura final es la de la piscina que no se ve prácticamente afectada por la del vaso, mientras que el agua del vaso cambia hasta igualarse a la de la piscina.

Idealmente, si la capacidad de un sistema $S 0$ es 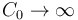$C_0\to\infty$ , su temperatura $T 0$ permanece constante sea cual sea la temperatura de otro sistema que ponemos en contacto con él. La temperatura del otro sistema, en cambio, cambia hasta igualarse a $T 0$ . Se dice entonces que $S 0$ es un baño térmico, foco o reservorio de calor.

Cuando se dice que el ambiente o entorno de un sistema se encuentra a una temperatura $T 0$ se presupone que este ambiente es un baño térmico de capacidad infinita. Por ello, su temperatura no se ve modificada por lo que le pase al sistema.

El que la temperatura del baño térmico no cambie no quiere decir que no entre o salga calor en él. Al contrario, lo que ocurre es que en un baño térmico puede entrar o salir todo el calor que sea necesario sin que se vea afectado. Por ello se denomina también “reservorio de calor”. Así, por ejemplo, al poner un sistema de capacidad $C 1$ en contacto con un baño de capacidad $C 0$ la temperatura final es

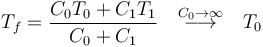
$T_f = \frac{C_0T_0+C_1T_1}{C_0+C_1} \quad \stackrel{C_0\to\infty}{\longrightarrow}\quad T_0$

y el calor que entra en el sistema

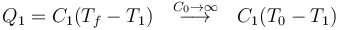
$Q_1 = C_1(T_f-T_1) \quad \stackrel{C_0\to\infty}{\longrightarrow}\quad C_1(T_0-T_1)\,$

y en el baño

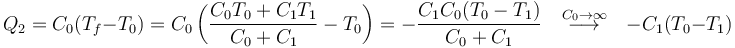
$Q_2 = C_0(T_f-T_0) = C_0\left(\frac{C_0T_0+C_1T_1}{C_0+C_1}-T_0\right)=-\frac{C_1C_0(T_0-T_1)}{C_0+C_1} \quad \stackrel{C_0\to\infty}{\longrightarrow}\quad -C_1(T_0-T_1)$

Vemos que efectivamente es el baño el que proporciona el calor, aunque no cambie su temperatura.

Lo mismo ocurre si el calor que entra en el sistema se emplea en un cambio de fase o para producir trabajo. En todos los casos el calor sale de un baño o reservorio, que no se ve afectado (idealmente).

10 Paredes y procesos adiabáticos

Cuando un sistema no experimenta cambios pese a ponerse en contacto con otros a diferente temperatura, porque sus paredes lo impiden, se dice que está aislado térmicamente y que las paredes son adiabáticas. A través de una frontera adiabática

$Q=0\,$

No existen las paredes perfectamente adiabáticas, como veremos al considerar la transmisión de calor, pero se pueden conseguir buenas aproximaciones. Una muy común es el vaso Dewar, que constituye la base de los termos de café. Se trata de dos frascos, uno contenido dentro de los cuales existe aire (si es posible a baja presión, haciendo el vacío parcialmente). Es el mismo esquema de las ventanas y paredes con cámara de aire. Para reducir aun más el posible flujo de calor, las superficies interiores pueden estar metalizadas.

Es costumbre, por el principio de los vasos Dewar, indicar las paredes adiabáticas en las ilustraciones mediante una línea doble, frente a las paredes diatermas, que se representan por una línea sencilla. Así, en las ilustraciones de la figura, el caso de arriba representaría dos cámaras de gas que no están aisladas entre sí ni con el exterior; en el caso intermedio está aisladas del exterior, pero no entre sí; en el caso inferior el aislamiento térmico de cada gas es total.

En un sistema aislado del exterior por paredes adiabáticas no puede haber calor entrando o saliendo del sistema y por tanto todos los procesos que ocurren en él se denomina adiabáticos.

Más en general un sistema experimenta un proceso adiabático cuando no intercambia calor con el ambiente, independientemente de si las paredes son aislantes o no. Así por ejemplo, en una compresión abrupta de un gas, éste no tiene tiempo para intercambiar calor con el entorno y la compresión se puede suponer adiabática. La compresión en los cilindros de un motor de explosión son un ejemplo típico, pero también lo son las ondas de sonido.

Los procesos adiabáticos pueden, como cualquier otro proceso, ser cuasiestáticos o no serlo.

Conviene tener clara la diferencia entre proceso isotermo y proceso adiabático:

Un proceso isotermo es aquél en que la temperatura permanece constante.
Un proceso adiabático es aquél en que no se intercambia calor entre el entorno y el sistema.

Podría pensarse que, si no se intercambia calor, la temperatura necesariamente permanece constante, pero no es así. Un proceso de cambio de fase producido por calor que entre desde el exterior es isotermo, pero no adiabático. La expansión de un gas en un recipiente aislado térmicamente del exterior es adiabático, pero no isotermo (al expandirse el gas se enfría).

11 Transferencia de calor

(Apéndice del tema 2 de Çengel & Bole, “Temas de especial interés”)

En los apartados anteriores se ha hablado del calor como de una transferencia de energía no asociada a variaciones en variables macroscópicas, pero no se ha dicho nada de cómo se transmite esa energía. Esto es, en el caso del trabajo uno “ve” cómo se realiza el trabajo (en el caso mecánico) o al menos posee un modelo del proceso (en el caso eléctrico), pero ¿cómo se transfiere el calor? ¿Cómo pasa esa energía de un cuerpo a otro?

Al estar asociado a variables microscópicas, cualquier descripción de la transferencia de calor debe basarse en el estudio de las colisiones e interacciones entre las moléculas de las diferentes sustancias, así como de la radiación que emiten (estando la radiación infrarroja usualmente asociada a la temperatura del cuerpo).

Independientemente de que se elabore un modelo microscópico más o menos detallado de las sustancias, sí pueden describirse las formas en que el calor se transmite de un cuerpo a otro. Estos mecanismo son:

Conducción
Convección
Radiación

Estos mecanismos no son incompatibles entre sí y de hecho es habitual que se den simultáneamente.

11.1 Conducción

La transmisión de calor por conducción se da cuando se ponen en contacto dos materiales a diferente temperatura.

La agitación térmica es mayor en el de temperatura más elevada, por lo que cuando se produce un choque de una de las moléculas de la superficie del más caliente con una de las moléculas superficiales del más frío, el que se movía más rápido pierde algo de su energía y el más lento la gana. El resultado es que la temperatura del más caliente disminuye y la del más frío aumenta. Se produce un flujo de energía a través de la superficie de contacto, que identificamos como calor.

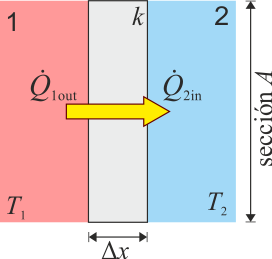
En su modelo más sencillo, suponemos que tenemos una lámina de un cierto material (por ejemplo, el vidrio de una ventana) a uno de cuyos lados se encuentra un sistema a una temperatura $T 2$ (por ejemplo, la calle a 15°C) y al otro uno a temperatura $T 2$ (la habitación, a 22°C). Se produce entonces un flujo de calor 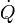$\dot{Q}$ (¡ojo al punto!) desde el sistema a mayor temperatura al de menor. ¿De qué depende este flujo de calor?

De la diferencia de temperaturas $Δ T = T 2 - T 1$ , cuánto mayor sea ésta, más grande es el flujo de calor.
Del espesor del material intermedio, $Δ x$ . Cuanto más grueso sea, menos calor fluye.
Del área $A$ del material. Por una ventana grande fluye más calor que por un ventanuco.
De la naturaleza del material intermedio. No fluye el mismo calor a través de una lámina metálica que a través de una de aislante de fibra de vidrio.

Todas estas propiedades se resumen en la siguiente fórmula, conocida como ley de Fourier:

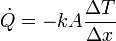
$\dot{Q} = -kA\frac{\Delta T}{\Delta x}$

donde 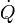$\dot{Q}$ es el flujo de calor considerando que va del medio 1 al 2, es decir, sería

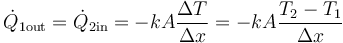
$\dot{Q}_{1\mathrm{out}}= \dot{Q}_{2\mathrm{in}}=-kA\frac{\Delta T}{\Delta x}=-kA\frac{T_2-T_1}{\Delta x}$

Si $T 1 > T 2$ entonces $Δ T > 0$ y el signo es positivo, como corresponde. Si $T 2 > T 1$ resulta un valor negativo, lo que implica que en ese caso el calor va del medio 2 al 1, como cabe esperar. Jugando con los signos, podemos escribir esta relación de forma simétrica apara los dos medios:

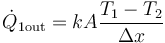
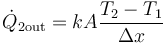
$\dot{Q}_{1\mathrm{out}}= kA\frac{T_1-T_2}{\Delta x}$ $\dot{Q}_{2\mathrm{out}}= kA\frac{T_2-T_1}{\Delta x}$

es decir, el calor que escapa de un sistema es proporcional a la diferencia entre la temperatura de ese sistema y la de lo que le rodea.

La constante $k$ es una propiedad de cada material denominada conductividad térmica. Se mide en el SI en W/(K·m). Valores aproximados para algunos materiales conocidos son

Material	$k$ (W/(K·m))	Material	$k$ (W/(K·m))	Material	$k$ (W/(K·m))
Aire seco	0.024	Agua	0.58	Cobre	385.0
Lana	0.04	Ladrillo	∼0.6	Hierro	80
Microfibra	0.033	Madera	∼0.15	Vidrio	0.96

Vemos que los metales son excelentes conductores del calor, mientras que los tejidos y el aire son aislantes térmicos.

Es la conductividad térmica y no la temperatura la que provoca que al pisar el suelo al levantarnos nos parezca frío, mientras que una zapatilla nos parece caliente. El suelo y la zapatilla están a la misma temperatura, pero mientras el calor se escapa de nuestros pies por el suelo, queda bloqueado por la zapatilla. Por la misma razón sería incorrecto hablar del calor que dan las mantas. Una manta actúa como un aislante térmico para que no se escape el calor humano, pero no producen calor por sí mismas.

11.1.1 Distribución de temperaturas

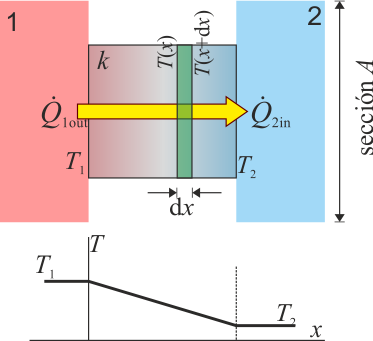
Consideremos el caso de una barra metálica, uno de cuyos extremos está en contacto con una fuente de calor, mientras que el otro se encuentra sumergido en agua con hielo. Sabemos que se producirá un flujo de calor a través del metal desde la fuente de calor hasta el sumidero, pero podemos decir más: la temperatura de la barra metálica no será la misma en todos los puntos (no estará, por tanto, en equilibrio térmico), sino que varía gradualmente desde su valor mínimo al máximo.

Si consideramos un corte de la barra de espesor diferencial $d x$ , el flujo de calor que lo atraviesa cumplirá la ley de Fourier, pero para una diferencia de temperaturas muy pequeña (la que hay entre $x$ y $x + d x$ ), con lo que obtenemos una relación con la derivada de la temperatura respecto a la posición

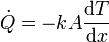
$\dot{Q}=-kA\frac{\mathrm{d}T}{\mathrm{d}x}$

Esta se conoce también como ley de Fourier y nos permite determinar, con las condiciones adecuadas, cuál es la distribución de temperaturas dentro de un sistema en presencia de flujos de calor.

En el caso de una capa de material situada entre dos focos a diferente temperatura, el resultado es que la temperatura varía linealmente con la posición.

11.1.2 Resistencia térmica

En el caso anterior de una lámina entre dos sistemas a diferente temperatura, existe una relación de proporcionalidad entre flujo de calor y temperatura que se puede escribir

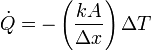
$\dot{Q}=-\left(\frac{kA}{\Delta x}\right)\Delta T$

La cantidad entre paréntesis no depende de la diferencia de temperaturas sino solo de las propiedades físicas y las dimensiones del material. A la inversa de este factor se lo denomina resistencia térmica de la lámina

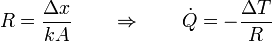
$R = \frac{\Delta x}{kA}\qquad\Rightarrow\qquad \dot{Q}=-\frac{\Delta T}{R}$

La resistencia térmica (que se mide en K/W) es una medida de la oposición al paso de calor. Cuanto mayor es el espesor de la lámina, menor su conductividad térmica o su área, menor es el flujo de calor. Un recubrimiento que tenga una resistencia térmica muy alta será un buen aislante térmico (una pared adiabática), mientras que si es muy baja (un envase metálico, por ejemplo) constituirá una pared diaterma.

Resistencias en paralelo: Consideremos el caso de una habitación. Parte de su frontera será ladrillo, parte vidrio, parte madera… El flujo de calor que entra en la habitación será la suma del que atraviesa cada uno de los materiales

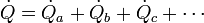
$\dot{Q}=\dot{Q}_a+\dot{Q}_b+\dot{Q}_c+\cdots$

Si todo el interior está a la misma temperatura

T int

y todo el exterior a una sola temperatura exterior

T ext

, entonces la diferencia de temperaturas a los lados de cada material es la misma para todos ellos

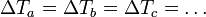
$\Delta T_a = \Delta T_b = \Delta T_c=\dots\,$

Por tanto nos queda

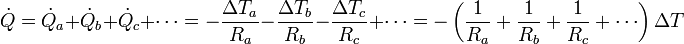
$\dot{Q}=\dot{Q}_a+\dot{Q}_b+\dot{Q}_c+\cdots=-\frac{\Delta T_a}{R_a}-\frac{\Delta T_b}{R_b}-\frac{\Delta T_c}{R_c}+\cdots=-\left(\frac{1}{R_a}+\frac{1}{R_b}+\frac{1}{R_c}+\cdots\right)\Delta T$

Si consideramos la resistencia del conjunto de la frontera verifica

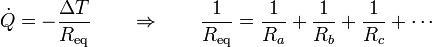
$\dot{Q}=-\frac{\Delta T}{R_\mathrm{eq}}\qquad\Rightarrow\qquad \frac{1}{R_\mathrm{eq}}=\frac{1}{R_a}+\frac{1}{R_b}+\frac{1}{R_c}+\cdots$

Por tanto, cuando tenemos resistencias térmicas en paralelo, la inversa de la resistencia equivalente es igual a la suma de las respectivas inversas.

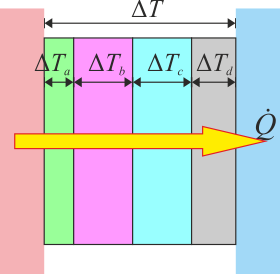
Resistencias en serie: Consideremos ahora varias capas puestas a continuación una de la otra, como pueden ser una sábana, dos mantas y un edredón. En este caso, no se cumple que el flujo de calor sea la suma de los flujos individuales, sino por el contrario, que el mismo calor que atraviesa la sábana, atraviesa las mantas y el edredón

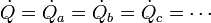
$\dot{Q}=\dot{Q}_a=\dot{Q}_b=\dot{Q}_c=\cdots$

La diferencia de temperaturas en cambio, será la suma de las sucesivas diferencias de temperatura

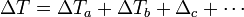
$\Delta T = \Delta T_a+\Delta T_b+\Delta_c +\cdots\,$

esto nos da la relación

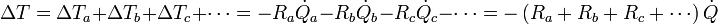
$\Delta T = \Delta T_a+\Delta T_b+\Delta T_c +\cdots = -R_a\dot{Q}_a-R_b\dot{Q}_b-R_c\dot{Q}_c-\cdots = -\left(R_a+R_b+R_c+\cdots\right)\dot{Q}$

según la cual la resistencia térmica equivalente a varias capas puestas en serie es la suma de las resistencias respectivas

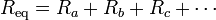
$R_\mathrm{eq}=R_a+R_b+R_c+\cdots\,$

El efecto entonces de colocar diversas capas sobre la piel no es reducir la diferencia de temperaturas con el exterior, que permanece constante, sino disminuir el flujo de calor. El calor que escapa del cuerpo debe ser repuesto por el organismo a partir de su metabolismo. Si este flujo es excesivo, el cuerpo no es capaz de compensarlo y sobreviene la hipotermia.

11.2 Convección

A la vista de las conductividades térmicas de la tabla anterior, es claro que el aire es más aislante que los tejidos, con lo cual surge la pregunta, ¿por qué nos vestimos? ¿por qué es necesario taparse con una manta en invierno, si el aire es más aislante que la lana?

La razón es que en un sistema fluido, como un gas o un líquido, la conducción no es el único mecanismo de transmisión de calor. Además de este, está presente la convección, que es la transferencia de energía arrastrada por el propio movimiento del fluido.

Consideremos el caso de una habitación, en la cual se encuentra un radiador, que calienta el aire a su alrededor. Si tuviéramos que esperar que el calor llegara por conducción al otro lado de la habitación, probablemente podríamos morir congelados. Lo que ocurre en realidad es que, al ser el aire caliente menos denso que el frío, asciende hacia el techo de la habitación, creando una depresión que es llenada por aire frío, el cual es calentado a su vez, continuando el proceso. Se establece así una circulación de corriente en forma de rollo. El efecto neto es la transmisión de calor desde el radiador hasta el otro extremo de la habitación. A este fenómeno se lo denomina “convección” y al movimiento del aire (o del fluido en general) se lo denomina “corriente de convección”.

Las corrientes de convección son responsables de fenómenos como la brisa, que durante el día va desde el mar hacia la tierra y durante la noche a la inversa.

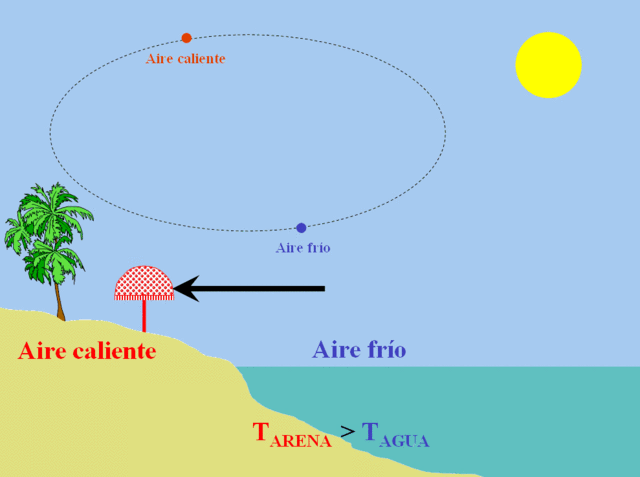
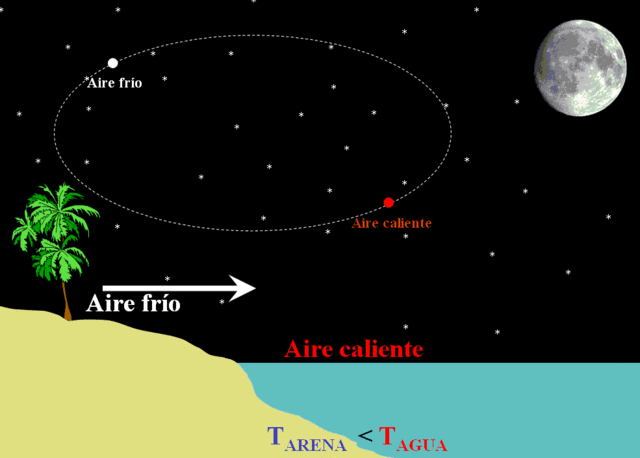
También son las causantes de la deriva de los continentes, arrastrados por las corrientes de convección del manto.

No es posible escribir una ecuación sencilla para la cantidad de calor transportada por convección, ya que depende de la solución del problema de dinámica de fluidos que implica el estudio de las corrientes de convección.

Cuando las corrientes de convección se producen espontáneamente, por la acción de la gravedad, la convección se denomina libre (o natural). Si es causada por algún agente externo, como un ventilador, se llama “convección forzada”.

La razón entonces de las mantas en invierno es tanto funcionar como aislante térmico como impedir que el aire en las proximidades del cuerpo humano escape. Sin ningún tipo de abrigo, el aire caliente próximo al cuerpo asciende por convección y es sustituido por aire frío, refrigerando el organismo.

Inversamente, el efecto de un ventilador en verano es forzar la convección y refrescar el cuerpo sustituyendo el aire caliente y húmedo que lo rodea por aire más fresco y seco (en este caso también es muy importante el efecto de la evaporación ya que, como se ha dicho, el cambio de fase requiere una gran cantidad de calor, que se extrae del organismo).

11.3 Radiación

El tercer mecanismo de transmisión de calor es la radiación. Todo cuerpo, por estar a una cierta temperatura, emite ondas electromagnéticas, pudiendo también absorberlas. La emisión de estas ondas por un cuerpo y su absorción por otro implica una transmisión de energía que identificamos como calor.

La longitud de onda y la potencia relativa de la radiación emitida depende de la temperatura del cuerpo, según la llamada ley del cuerpo negro. Para las temperaturas habituales a nuestro alrededor, la mayor parte de esta radiación está en la banda de infrarrojos. Por ello, las cámaras de visión nocturna y los termogramas se basan en la detección de radiación infrarroja, de forma que se asocia un calor a cada longitud de onda y por tanto a cada temperatura.

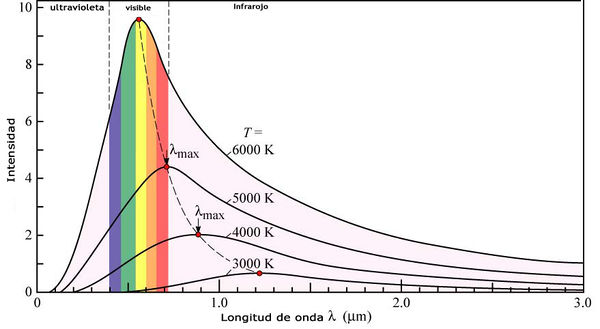
Para cuerpos a altas temperaturas, la radiación térmica emitida entra en el espectro visible y por ello tenemos “hierro al rojo vivo”. Una mayor temperatura supone emisión centrada en el naranja (como en el Sol) o incluso en colores de longitudes de onda más corta. De esta forma, a partir del color de una estrella se conoce su temperatura exterior.

La potencia emitida por un cuerpo en forma de radiación depende su temperatura según la llamada ley de Stefan-Boltzmann. Para un cuerpo negro ideal

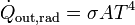
$\dot{Q}_\mathrm{out,rad} = \sigma A T^4$

donde $A$ es el área del cuerpo y

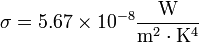
$\sigma = 5.67\times 10^{-8}\frac{\mathrm{W}}{\mathrm{m}^2\cdot\mathrm{K}^4}$

es una constante universal conocida como constante de Stefan-Boltzmann. En un cuerpo real, la radiación emitida nunca alcanza este valor, por lo que se escribe

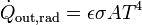
$\dot{Q}_\mathrm{out,rad} = \epsilon\sigma A T^4$

siendo $ε$ una cantidad entre 0 y 1 denominada emisividad del cuerpo. El que la potencia radiada vaya como la cuarta potencia de la temperatura absoluta quiere decir que a bajas temperaturas el calor emitido o absorbido por radiación puede ser despreciable, pero a altas temperaturas puede ser el factor dominante.

La emisión por radiación no puede ser impedida nunca de manera completa, ya que el simple hecho de tener una temperatura provoca emisión de radiación. Por ello es imposible construir unas paredes totalmente adiabáticas. Sí puede ser reducida con ayuda de paredes reflectantes que devuelvan parte de la radiación emitida (por ello, las paredes de la cámara de los termos o vasos Dewar están metalizadas).

Si consideramos un cuerpo a temperatura $T 1$ rodeado de un ambiente a temperatura $T 0$ , el calor que entra en el cuerpo por radiación será

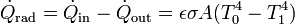
$\dot{Q}_\mathrm{rad}=\dot{Q}_\mathrm{in}-\dot{Q}_\mathrm{out}=\epsilon \sigma A(T_0^4-T_1^4)$

Si la temperatura del entorno es superior a la del cuerpo se produce absorción neta de calor por radiación, mientras que si el cuerpo está a mayor temperatura que el ambiente es a la inversa, como cabe esperar.

Las pérdidas de energía por radiación son responsables del “relente”: el fenómeno de que en una noche despejada un objeto situado en la calle (un coche aparcado, por ejemplo) puede estar más frío que el aire circundante. La razón de este desequilibrio térmico se debe a que en este caso el “entorno” es el vacío interplanetario, que se encuentra a una temperatura de 2.7K. Por ello, la radiación que emite el vehículo hacia el espacio es mucho mayor que la que puede recibir de él y se produce un enfriamiento continuado. Si desapareciera el Sol, este efecto congelaría la Tierra entera rápidamente.

$\quad$

El relente no se produce en una noche cubierta, ya que en ese caso la radiación emitida por el coche se refleja en las nubes, que funcionan como entorno. Aunque las nubes también se enfrían, la capa de aire entre ellas y el suelo mantiene una temperatura mucho más alta que en el caso de una noche despejada.

12 Dependencia del camino

El calor, como el trabajo, es una cantidad que depende del proceso y no solo de los estados inicial y final.

A modo de ejemplo, consideremos el mismo ejemplo que se ve en el caso del trabajo: un gas que ocupa inicialmente un volumen $V A$ a una presión $p A$ y temperatura $T A$ . Este gas se comprime cuasiestáticamente hasta que su volumen vale $V B = V A / 2$ a una presión $p B = 2 p A$ . ¿Cuanto calor entra en el gas?

Estas son algunas de las posibilidades:

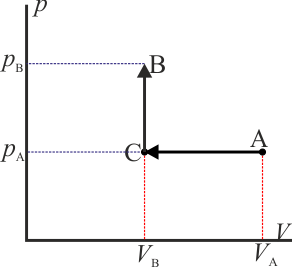
Proceso isóbaro seguido de proceso isócoro: Podemos comprimir el gas a presión constante, bajando su temperatura, hasta que su volumen es la mitad del inicial. A partir de ahí lo volvemos a calentar a volumen constante hasta que la presión se eleva al doble. Gráficamente corresponde a una recta horizontal seguida de un segmento vertical, siendo C el vértice intermedio. El calor que entra es suma de dos contribuciones:

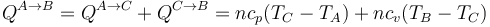
$Q^{A\to B}= Q^{A\to C}+Q^{C\to B}= nc_p(T_C-T_A)+nc_v(T_B-T_C)\,$

Para poner este resultado en términos de la presión y el volumen hacemos uso de la relación de las capacidades específicas molares con la constante universal de los gases ideales

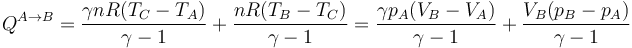
$Q^{A\to B}=\frac{\gamma nR(T_C-T_A)}{\gamma-1}+\frac{nR(T_B-T_C)}{\gamma-1}=\frac{\gamma p_A(V_B-V_A)}{\gamma-1}+\frac{V_B(p_B-p_A)}{\gamma-1}$

que para este estado final concreto da

$Q^{A\to B}=\frac{\gamma p_A(V_A/2-V_A)}{\gamma-1}+\frac{(V_A/2)(2p_A-p_A)}{\gamma-1}=\frac{p_AV_A}{2}$

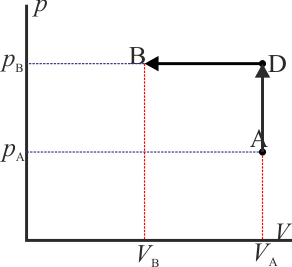
Proceso isócoro seguido de proceso isóbaro: Alternativamente, podemos empezar calentando el gas hasta que su presión sea el doble de la inicial (estado D) y luego enfriarlo hasta que se volumen se reduzca a la mitad. Gráficamente es un segmento vertical seguido de uno horizontal, siendo D el estado intermedio. El calor es ahora

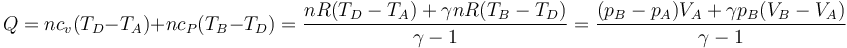
$Q=nc_v(T_D-T_A)+nc_P(T_B-T_D)=\frac{nR(T_D-T_A)+\gamma n R(T_B-T_D)}{\gamma-1}=\frac{(p_B-p_A)V_A+\gamma p_B(V_B-V_A)}{\gamma-1}$

que para este estado final vale

$Q=\frac{(2p_A-p_A)V_A+\gamma (2p_A)(V_A/2-V_A)}{\gamma-1}=p_AV_A$

@@ Línea 415: / Línea 415: @@
 <center><math>C_1(T_f-T_1) +C_2(T_f-T_2) = 0\qquad\Rightarrow\qquad T_f = \frac{C_1 T_1+C_2T_2}{C_1+C_2}</math></center>
+Gráficamente, sería lo siguiente: Tenemos inicialmente dos subsistemas a temperaturas diferentes, el calor que entra en el 1 sale del 2. Esto se ve como una recta creciente, para la temperatura del medio 1 y una decreciente para la del medio 2. Inicialmente cada parte tiene una temperatura distinta. El equilibrio se alcanza cuando las rectas se cortan. El valor del calor en ese punto es el que sale de una parte y entra en la otra.
+<center>[[Archivo:capacidad-calorifica-02.png]]</center>
 Si sí hay cambio de fase, es preciso analizar si el calor que sale de uno de los sistemas es suficiente para producir un cambio de fase de toda la sustancia o de solo una parte de ella. Por ejemplo, si ponemos en contacto 1&thinsp;kg de hielo a 0&deg;C con 1&thinsp;kg de agua a 10&deg;C, del agua solo salen 41.8&thinsp;kJ, cuando se necesitan 334&thinsp;kJ para fundir todo el hielo. Por ello, solo se funden 41.8/334 = 0.125&thinsp;kg y el resultado final son 875&thinsp;g de hielo y 1125&thinsp;g de agua, ambos a 0&deg;C.