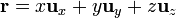Coordenadas cartesianas. Base vectorial
De Laplace
(→Vectores de la base) |
|||
| Línea 3: | Línea 3: | ||
<center><math>\mathbf{u}_x = \mathbf{i}\qquad \mathbf{u}_y = \mathbf{j}\qquad \mathbf{u}_z = \mathbf{k}</math></center> | <center><math>\mathbf{u}_x = \mathbf{i}\qquad \mathbf{u}_y = \mathbf{j}\qquad \mathbf{u}_z = \mathbf{k}</math></center> | ||
| + | |||
| + | ==Base ortonormal dextrógira== | ||
| + | |||
| + | Los vectores de la base cartesiana forman una [[base ortonormal dextrógira]] si se ordenan en la forma tradicional <math>\left{\mathbf{u}_x,\mathbf{u}_y,\mathbf{u}_z\right}</math>. Los productos escalares vienen dados por las siguientes tablas de multiplicar | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! · | ||
| + | ! <math>\mathbf{u}_x</math> | ||
| + | ! <math>\mathbf{u}_y</math> | ||
| + | ! <math>\mathbf{u}_z</math> | ||
| + | |- | ||
| + | | row 1, cell 1 | ||
| + | | row 1, cell 2 | ||
| + | | row 1, cell 3 | ||
| + | |- | ||
| + | | row 2, cell 1 | ||
| + | | row 2, cell 2 | ||
| + | | row 2, cell 3 | ||
| + | |} | ||
==Factores de escala== | ==Factores de escala== | ||
Revisión de 19:11 21 nov 2007
Contenido |
1 Vectores de la base
Para el sistema cartesiano la construcción es inmediata. En cada punto del espacio las líneas coordenadas son rectas paralelas a los ejes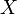 
, 
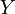y 
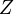. Por tanto, los vectores de la base cartesiana son nuestros viejos conocidos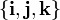 
2 Base ortonormal dextrógira
Los vectores de la base cartesiana forman una base ortonormal dextrógira si se ordenan en la forma tradicional No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \left{\mathbf{u}_x,\mathbf{u}_y,\mathbf{u}_z\right} . Los productos escalares vienen dados por las siguientes tablas de multiplicar
| · | 
| 
| 
|
|---|---|---|---|
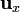
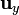
| row 1, cell 1 | row 1, cell 2 | row 1, cell 3 | |
| row 2, cell 1 | row 2, cell 2 | row 2, cell 3 |
3 Factores de escala
Los factores de escala en este sistema también son sencillos. Puesto que las coordenadas representan distancias a los planos coordenados, si nos desplazamos una cantidad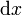 
a lo largo de la línea coordenada 
, la distancia que recorremos es... ¡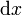!. Lo mismo con 
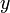y con
. Por tanto, los factores de escala para las tres coordenadas valen
Las coordenadas cartesianas poseen una propiedad que las hace diferentes del resto de sistemas de coordenadas:
4 Vector de posición
El vector de posición en la base cartesiana y en componentes cartesianas se escribe
