Problemas de herramientas matemáticas (GIE)
De Laplace
(→Ejemplo de velocidad en función de la posición) |
(→Trabajo en una semicircunferencia) |
||
| Línea 141: | Línea 141: | ||
cuando la partícula pasa de <math>\vec{r}_A=R\vec{k}</math> a <math>\vec{r}_B=-R\vec{k}</math> moviéndose sobre una semicircunferencia vertical de radio <math>R</math> con centro el origen de coordenadas. | cuando la partícula pasa de <math>\vec{r}_A=R\vec{k}</math> a <math>\vec{r}_B=-R\vec{k}</math> moviéndose sobre una semicircunferencia vertical de radio <math>R</math> con centro el origen de coordenadas. | ||
| + | ==[[Variación de la presión atmosférica]]== | ||
| + | La presión atmosférica en un punto se debe al peso por unidad de superficie de la columna de aire situada sobre él. En un modelo de la atmósfera, se supone que la densidad del aire disminuye con la altura como | ||
| + | |||
| + | <center><math>\rho(z) = \rho_0\mathrm{e}^{-\alpha z}</math></center> | ||
| + | |||
| + | extendiéndose la altura hasta el infinito. | ||
| + | |||
| + | # Determine el peso del aire situado por encima de un cuadrado de lado <math>L</math> situado a una altura <math>z_0</math> sobre el nivel del mar. A partir de aquí halle como varía la presión atmosférica con la altura. | ||
| + | # Sabiendo que al nivel del mar la presión es de 101325 Pa y la densidad del aire es de 1.225 kg/m³, calcule el valor de la constante <math>\alpha</math>. | ||
| + | # Usando esta fórmula halle el valor de la presión atmosférica en La Paz, situada a 3650 m de altitud. | ||
| + | # Halle el valor aproximado de la masa de aire de la atmósfera. | ||
| + | |||
| + | En todos los pasos, razone los cálculos y justifique las aproximaciones que se hagan. | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)|0]] | [[Categoría:Problemas de herramientas matemáticas (GIE)|0]] | ||
[[Categoría:Herramientas matemáticas (GIE)]] | [[Categoría:Herramientas matemáticas (GIE)]] | ||
Revisión de 10:20 22 oct 2011
1 Arco capaz
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores 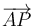 y
y
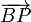 son ortogonales.
son ortogonales.
Inversamente, sean A, B y P tres puntos tales que 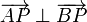 . Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.
. Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.
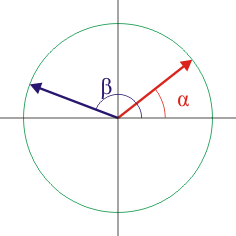
2 Coseno y seno de una diferencia
A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.
3 Construcción de una base
Dados los vectores

Construya una base ortonormal dextrógira 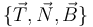 , tal que
, tal que
- El primer vector,
 , vaya en la dirección y sentido de
, vaya en la dirección y sentido de 
- El segundo,
 , esté contenido en el plano definido por
, esté contenido en el plano definido por  y
y  y apunte hacia el mismo semiplano (respecto de
y apunte hacia el mismo semiplano (respecto de  ) que el vector
) que el vector  .
.
- El tercero,
 , sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
, sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
4 Ejemplo de operaciones con dos vectores
Dados los vectores

- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
 como suma de dos vectores, uno paralelo a
como suma de dos vectores, uno paralelo a  y otro ortogonal a él.
y otro ortogonal a él.
5 Formulas vectoriales potencialmente incorrectas
De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de cálculo de dimensiones, R es una distancia y  el vector de posición; t es el tiempo:
el vector de posición; t es el tiempo:
- (a)
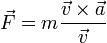
- (b)
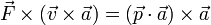
- (c)
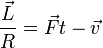
- (d)
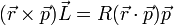
- (e)
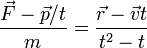
- (f)
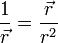
- (g)
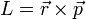
- (h)
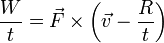
6 Determinación de un vector a partir de sus proyecciones
Se tiene un vector conocido, no nulo,  y uno que se desea determinar,
y uno que se desea determinar, 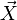 . Se dan como datos su producto escalar y su
producto vectorial por
. Se dan como datos su producto escalar y su
producto vectorial por 

Determine el valor de 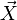 . ¿Es suficiente una sola de las dos ecuaciones para hallar
. ¿Es suficiente una sola de las dos ecuaciones para hallar 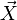 ?
?
7 Cálculo de las componentes de un vector
De una fuerza 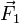 se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?
se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?
Si a esta fuerza se le suma otra 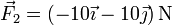 , ¿qué ángulo forma la resultante con los ejes coordenados?
, ¿qué ángulo forma la resultante con los ejes coordenados?
8 Cálculo numérico de la derivada del seno
Se trata de calcular la derivada de 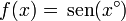 para
para 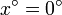 .
.
- Exprese el cociente Δf / Δx, cuando
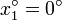 y
y 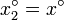 .
.
- Calcule numéricamente el cociente anterior para
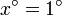 ,
, 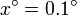 ,
, 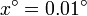 ,… hasta
,… hasta 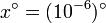 . ¿A cuanto tiende el límite?
. ¿A cuanto tiende el límite?
- Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de
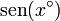 en
en 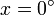 ?
?
9 Aproximación numérica de la velocidad y la aceleración
La posición de una partícula en distintos instantes de tiempo es, aproximadamente
| t (s) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x (m) | 0.00 | -0.04 | -0.06 | -0.06 | -0.04 | 0.00 | 0.06 | 0.14 | 0.24 | 0.36 | 0.50 |
- ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre
 y
y  .
.
- Calcule aproximadamente la aceleración en el mismo intervalo.
10 Ejemplo de velocidad en función de la posición
La velocidad de una partícula sigue la ley
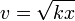
siendo x la distancia recorrida desde el instante inicial.
Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?
11 Cálculo de la masa de una esfera
La densidad de masa de una esfera de radio R viene dada por la ley

Sabiendo que el área de una superficie esférica de radio r vale 4πr2, calcule el volumen y la masa de la esfera de radio R. ¿Cuánto vale su densidad media?
12 Ejemplo de integración numérica
Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica
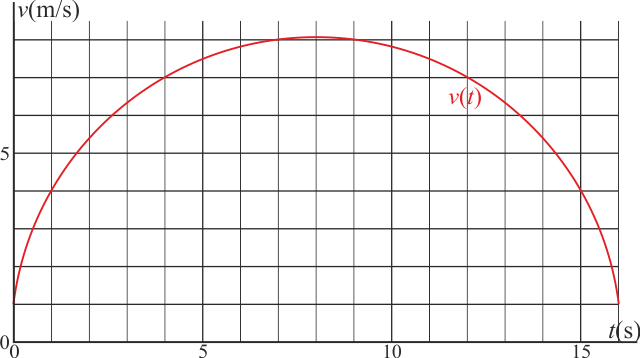
La partícula parte de s = 0.
- Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en
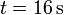 .
.
- Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es

- ¿Cuál es el error relativo cometido en el apartado anterior?
13 Trabajo en una semicircunferencia
Una partícula se encuentra sometida a su peso 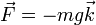 . Halle el trabajo realizado por esta fuerza
. Halle el trabajo realizado por esta fuerza
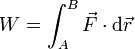
cuando la partícula pasa de  a
a 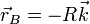 moviéndose sobre una semicircunferencia vertical de radio R con centro el origen de coordenadas.
moviéndose sobre una semicircunferencia vertical de radio R con centro el origen de coordenadas.
14 Variación de la presión atmosférica
La presión atmosférica en un punto se debe al peso por unidad de superficie de la columna de aire situada sobre él. En un modelo de la atmósfera, se supone que la densidad del aire disminuye con la altura como
extendiéndose la altura hasta el infinito.
- Determine el peso del aire situado por encima de un cuadrado de lado L situado a una altura z0 sobre el nivel del mar. A partir de aquí halle como varía la presión atmosférica con la altura.
- Sabiendo que al nivel del mar la presión es de 101325 Pa y la densidad del aire es de 1.225 kg/m³, calcule el valor de la constante α.
- Usando esta fórmula halle el valor de la presión atmosférica en La Paz, situada a 3650 m de altitud.
- Halle el valor aproximado de la masa de aire de la atmósfera.
En todos los pasos, razone los cálculos y justifique las aproximaciones que se hagan.





