Coordenadas cartesianas. Base vectorial
De Laplace
(Diferencias entre revisiones)
(→Base vectorial cartesiana) |
(→Factores de escala) |
||
| Línea 5: | Línea 5: | ||
==Factores de escala== | ==Factores de escala== | ||
| + | |||
| + | Los factores de escala en este sistema también son sencillos. Puesto que las coordenadas representan distancias a los planos coordenados, si nos desplazamos una cantidad <math>\mathrm{d}x\,</math> a lo largo de la línea coordenada <math>x\,</math>, la distancia que recorremos es... ¡<math>\mathrm{d}x\,</math>!. Lo mismo con <math>y\,</math> y con | ||
| + | <math>z\,</math>. Por tanto, los factores de escala para las tres coordenadas valen | ||
| + | |||
| + | <center><math>h_x = 1\qquad h_y = 1\qquad h_z = 1</math></center> | ||
| + | |||
| + | Las coordenadas cartesianas poseen una propiedad que las hace diferentes del resto de sistemas de coordenadas: | ||
| + | |||
| + | \textbf{la base cartesiana es independiente de la posición}. | ||
==Vector de posición== | ==Vector de posición== | ||
Revisión de 17:32 20 nov 2007
Contenido |
1 Vectores de la base
Para el sistema cartesiano la construcción es inmediata. En cada punto del espacio las líneas coordenadas son rectas paralelas a los ejes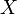 
, 
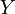y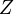 
. Por tanto, los vectores de la base cartesiana son nuestros viejos conocidos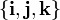 
2 Factores de escala
Los factores de escala en este sistema también son sencillos. Puesto que las coordenadas representan distancias a los planos coordenados, si nos desplazamos una cantidad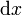 
a lo largo de la línea coordenada 
, la distancia que recorremos es... ¡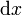!. Lo mismo con 
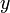y con
. Por tanto, los factores de escala para las tres coordenadas valen
Las coordenadas cartesianas poseen una propiedad que las hace diferentes del resto de sistemas de coordenadas:
\textbf{la base cartesiana es independiente de la posición}.
