Entrar Página Discusión Historial Go to the site toolbox

Entropía de una mezcla de gases

De Laplace

(Diferencias entre revisiones)
(→Entropía de un gas ideal)
(→Entropía de un gas ideal)
 
(11 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
Un recipiente de 2.00&thinsp;l tiene una barrera que lo divide por la mitad. Una mitad contiene H<sub>2</sub> y la otra O<sub>2</sub>. Ambos gases se encuentran a temperatura ambiente y presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?
+
Un recipiente de 2.00&thinsp;l tiene una barrera que lo divide por la mitad. Una mitad contiene H<sub>2</sub> y la otra O<sub>2</sub>. Ambos gases se encuentran a una temperatura de 25&deg;C y a la presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?
-
==Entropía de un gas ideal==
+
==Entropía de un solo gas==
-
===Expresión en función de T y V===
+
La variación de la [[Entropía#Gas_ideal|entropía de un gas ideal]] en función de la temperatura y el volumen es
-
Para un gas ideal puro, podemos calcular el incremento diferencial de entropía a partir de la definición
+
-
<center><math>\mathrm{d}S=\frac{\mathrm{d}Q_\mathrm{rev}}{T}</math></center>
+
<center><math>\Delta S = nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right)</math></center>
-
A su vez, el diferencial de calor reversible puede hallarse mediante el primer principio de la termodinámica
+
y, en función de la temperatura y la presión
-
<center><math>\mathrm{d}S=\frac{\mathrm{d}U-\mathrm{d}W}{T}</math></center>
+
<center><math>\Delta S = nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)</math></center>
-
Para un gas ideal sabemos que
+
Si tenemos un conjunto de moles de un gas que se expande de un volumen V a un volumen 2V, siendo la temperatura final la misma que la inicial, la variación en la entropía del gas es
-
<center><math>\mathrm{d}U = nc_V\,\mathrm{d}T</math>{{qquad}}{{qquad}}<math>\mathrm{d}W=-p\,\mathrm{d}V</math>{{tose}}<math>\mathrm{d}S=nc_V\frac{\mathrm{d}T}{T}+\frac{p}{T}\mathrm{d}V</math></center>
+
<center><math>\Delta S = nc_V\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}+nR\ln\left(\frac{2V}{V}\right) = nR\,\ln(2)</math></center>
-
Sustituyendo la ecuación de estado del gas ideal
+
Si usamos como variables la temperatura y la presión (que tienen la ventaja de ser ambas variables intensivas), lo que vemos es que la presión se reduce a la mitad
-
<center><math>\mathrm{d}S = nc_V\frac{\mathrm{d}T}{T}+nR\,\frac{\mathrm{d}V}{V}</math></center>
+
<center><math>\Delta S = nc_p\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}-nR\ln\left(\frac{p/2}{p}\right) = nR\,\ln(2)</math></center>
-
Si suponemos que la capacidad calorífica molar es independiente de la temperatura, podemos integrar esta ecuación para hallar el incremento entre dos estados
+
que naturalmente coincide con el resultado anterior.
-
<center><math>\Delta S = nc_V\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}+nR\int_{V_1}^{V_2}\frac{\mathrm{d}V}{V}= nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right)</math></center>
+
==Entropía de una mezcla==
 +
La entropía es una propiedad extensiva. Para una sustancia pura esto quiere decir que es proporcional a la cantidad de sustancia, esto es, es proporcional a la masa. Para una mezcla de gases ideales, se comportará como lo hace la masa de la mezcla.
-
===Expresión en función de T y p===
+
Si tenemos N sustancias, con <math>n_i</math> moles de cada una, con una masa molar <math>m_i</math>, la masa total será
-
Si lo que tenemos es el cambio en la presión, en lugar del volumen, podemos hacer un cálculo análogo empleando la entalpía
+
-
<center><math>\mathrm{d}S=\frac{\mathrm{d}Q_\mathrm{rev}}{T}=\frac{\mathrm{d}H-V\,\mathrm{d}p\mathrm{d}W}{T}</math></center>
+
<center><math>m = \sum_{i=1}^N n_im_i</math></center>
-
La entalpía se relaciona con la temperatura a través de la capacidad calorífica a presión constante
+
así que la entropía de la mezcla será
-
<center><math>\mathrm{d}H = nc_p\,\mathrm{d}T</math></center>
+
<center><math>S = \sum_{i=1}^N n_is_i</math></center>
-
lo que lleva a la expresión para el incremento de entropía
+
siendo <math>s_i</math> la entropía por mol de la sustancia <math>i</math>. Una forma análoga tendremos para el incremento de la entropía.
-
<center><math>\Delta S = nc_p\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}-nR\int_{p_1}^{p_2}\frac{\mathrm{d}p}{p}= nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)</math></center>
+
<center><math>\Delta S = \sum_{i=1}^N n_i\,\Delta s_i</math></center>
-
También se puede llegar a este resultado sustituyendo la ecuación de los gases ideales en la expresión en función de T y V.
+
El incremento de la entropía molar para cada sustancia será
-
===Expansión adiabática===
+
<center><math>\Delta s_i = \frac{\Delta S_i}{n_i}= c_{pi}\ln\left(\frac{T_i}{T_{i0}}\right)-R\ln\left(\frac{p_{i}}{p_{i0}}\right)</math></center>
-
Si tenemos un conjunto de moles de un gas que se expande de un volumen V a un volumen 2V, siendo la temperatura final la misma que la inicial, la variación en la entropía del gas es
+
-
<center><math>\Delta S =  nc_V\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}+nR\ln\left(\frac{2V}{V}\right) = nR\,\ln(2)</math></center>
+
donde las <math>p_i</math> son las presiones ''parciales'' de los gases de la mezcla, es decir,
-
Si usamos como variables la temperatura y la presión (que tienen la ventaja de ser ambas variables intensivas), lo que vemos es que la presión se reduce a la mitad
+
<center><math>p_i = x_i p\,</math>{{qquad}}{{qquad}}<math>x_i = \frac{n_i}{\sum_i n_i}</math></center>
-
<center><math>\Delta S =  nc_p\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}-nR\ln\left(\frac{p/2}{p}\right) = nR\,\ln(2)</math></center>
+
con lo que el incremento de la entropía total es
-
que naturalmente coincide con el resultado anterior.
+
<center><math>\Delta S = \sum_{i=1}^N\left(n_ic_{p_i}\ln\left(\frac{T_i}{T_{i0}}\right)-n_iR\ln\left(\frac{p_{i}}{p_{i0}}\right)\right)</math></center>
-
==Entropía de una mezcla==
+
==Incremento de entropía==
 +
En nuestro caso, la temperatura inicial es la misma que la final para los dos gases.
 +
<center><math>T_{i}=T_{i0}\,</math>{{tose}}<math>\ln\left(\frac{T_i}{T_{i0}}\right)=0</math></center>
 +
Lo mismo ocurre con la presión ''total'' ('''no''' con la parcial), ya que inicialmente ambos se encontraban a la misma y al romper la membrana se redistribuyen las moléculas, pero el número de moles total y el volumen total sigue siendo el mismo.
-
==Incremento de entropía==
+
<center><math>p_{i0}=p\,</math></center>
 +
 
 +
Las presiones parciales sí se ven reducidas pues cada gas pasa a ocupar el volumen total, con el mismo número de moles. las presiones parciales serán
 +
 
 +
<center><math>p_i = x_i p = x_i p_{i0}\,</math></center>
 +
 
 +
Todo esto deja el aumento de entropía en
 +
 
 +
<center><math>\Delta S = \sum_i n_ic_{pi}\overbrace{\ln\left(\frac{T_i}{T_{i0}}\right)}^{=0}-\sum_i n_i R \ln\left(\frac{p_i}{p_{i0}}\right) = -\sum_i n_i R \ln\left(x_i\right)</math></center>
 +
 
 +
Aplicando la ley de los gases ideales
 +
 
 +
<center><math>\Delta S = -\sum_i\frac{p_iV}{T}\ln(x_i) = -\frac{pV}{T}\left(x_{O_2}\ln(x_{O_2})+x_{H_2}\ln(x_{H_2})\right)</math></center>
 +
 
 +
En nuestro caso, las fracciones molares de los dos gases son la misma: un 50%, ya que a igualdad de presión, volumen y temperaturas iniciales les corresponde el mismo número de moles (nótese que no necesitamos calcular cuántos son estos moles).
 +
 
 +
<center><math>x_{O_2}=x_{H_2} = \frac{1}{2}</math>{{tose}}<math>\Delta S = -\frac{1\,\mathrm{atm}\cdot 2\,\mathrm{l}}{298\,\mathrm{K}}(2\times(0.5\ln(0.5))\cdot\frac{101.325\,\mathrm{J}}{1\,\mathrm{atm}\cdot\mathrm{l}} = 0.471\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 
 +
Vemos que la entropía del universo aumenta, ya que la del sistema lo hace y la del ambiente no se ve afectada (no hay intercambio de calor con el exterior). Por ello, este proceso de mezcla es espontáneo e irreversible.
[[Categoría:Problemas del segundo principio de la termodinámica]]
[[Categoría:Problemas del segundo principio de la termodinámica]]

última version al 11:18 17 may 2009

Contenido

1 Enunciado

Un recipiente de 2.00 l tiene una barrera que lo divide por la mitad. Una mitad contiene H2 y la otra O2. Ambos gases se encuentran a una temperatura de 25°C y a la presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?

2 Entropía de un solo gas

La variación de la entropía de un gas ideal en función de la temperatura y el volumen es

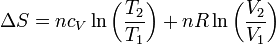
\Delta S = nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right)

y, en función de la temperatura y la presión

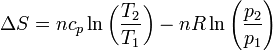
\Delta S = nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)

Si tenemos un conjunto de moles de un gas que se expande de un volumen V a un volumen 2V, siendo la temperatura final la misma que la inicial, la variación en la entropía del gas es

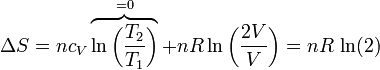
\Delta S = nc_V\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}+nR\ln\left(\frac{2V}{V}\right) = nR\,\ln(2)

Si usamos como variables la temperatura y la presión (que tienen la ventaja de ser ambas variables intensivas), lo que vemos es que la presión se reduce a la mitad

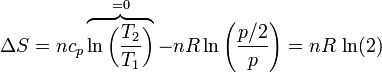
\Delta S = nc_p\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}-nR\ln\left(\frac{p/2}{p}\right) = nR\,\ln(2)

que naturalmente coincide con el resultado anterior.

3 Entropía de una mezcla

La entropía es una propiedad extensiva. Para una sustancia pura esto quiere decir que es proporcional a la cantidad de sustancia, esto es, es proporcional a la masa. Para una mezcla de gases ideales, se comportará como lo hace la masa de la mezcla.

Si tenemos N sustancias, con ni moles de cada una, con una masa molar mi, la masa total será

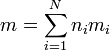
m = \sum_{i=1}^N n_im_i

así que la entropía de la mezcla será

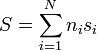
S = \sum_{i=1}^N n_is_i

siendo si la entropía por mol de la sustancia i. Una forma análoga tendremos para el incremento de la entropía.

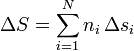
\Delta S = \sum_{i=1}^N n_i\,\Delta s_i

El incremento de la entropía molar para cada sustancia será

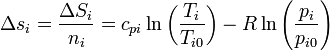
\Delta s_i = \frac{\Delta S_i}{n_i}= c_{pi}\ln\left(\frac{T_i}{T_{i0}}\right)-R\ln\left(\frac{p_{i}}{p_{i0}}\right)

donde las pi son las presiones parciales de los gases de la mezcla, es decir,

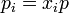
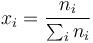
p_i = x_i p\,        x_i = \frac{n_i}{\sum_i n_i}

con lo que el incremento de la entropía total es

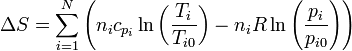
\Delta S = \sum_{i=1}^N\left(n_ic_{p_i}\ln\left(\frac{T_i}{T_{i0}}\right)-n_iR\ln\left(\frac{p_{i}}{p_{i0}}\right)\right)

4 Incremento de entropía

En nuestro caso, la temperatura inicial es la misma que la final para los dos gases.

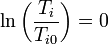
T_{i}=T_{i0}\,   \Rightarrow   \ln\left(\frac{T_i}{T_{i0}}\right)=0

Lo mismo ocurre con la presión total (no con la parcial), ya que inicialmente ambos se encontraban a la misma y al romper la membrana se redistribuyen las moléculas, pero el número de moles total y el volumen total sigue siendo el mismo.

p_{i0}=p\,

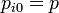
Las presiones parciales sí se ven reducidas pues cada gas pasa a ocupar el volumen total, con el mismo número de moles. las presiones parciales serán

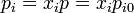
p_i = x_i p = x_i p_{i0}\,

Todo esto deja el aumento de entropía en

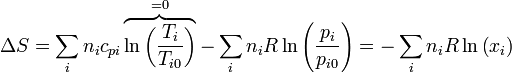
\Delta S = \sum_i n_ic_{pi}\overbrace{\ln\left(\frac{T_i}{T_{i0}}\right)}^{=0}-\sum_i n_i R \ln\left(\frac{p_i}{p_{i0}}\right) = -\sum_i n_i R \ln\left(x_i\right)

Aplicando la ley de los gases ideales

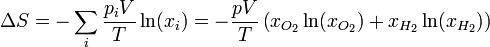
\Delta S = -\sum_i\frac{p_iV}{T}\ln(x_i) = -\frac{pV}{T}\left(x_{O_2}\ln(x_{O_2})+x_{H_2}\ln(x_{H_2})\right)

En nuestro caso, las fracciones molares de los dos gases son la misma: un 50%, ya que a igualdad de presión, volumen y temperaturas iniciales les corresponde el mismo número de moles (nótese que no necesitamos calcular cuántos son estos moles).

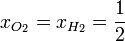
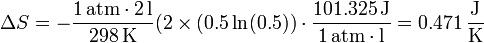
x_{O_2}=x_{H_2} = \frac{1}{2}   \Rightarrow   \Delta S = -\frac{1\,\mathrm{atm}\cdot 2\,\mathrm{l}}{298\,\mathrm{K}}(2\times(0.5\ln(0.5))\cdot\frac{101.325\,\mathrm{J}}{1\,\mathrm{atm}\cdot\mathrm{l}} = 0.471\,\frac{\mathrm{J}}{\mathrm{K}}

Vemos que la entropía del universo aumenta, ya que la del sistema lo hace y la del ambiente no se ve afectada (no hay intercambio de calor con el exterior). Por ello, este proceso de mezcla es espontáneo e irreversible.

Obtenido de "http://tesla.us.es/wiki/index.php/Entrop%C3%ADa_de_una_mezcla_de_gases"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:18, 17 may 2009. - Esta página ha sido visitada 45.197 veces. - Aviso legal - Acerca de Laplace