Problemas del primer principio de la termodinámica
De Laplace
(→Mezcla de agua y hielo) |
|||
| (18 ediciones intermedias no se muestran.) | |||
| Línea 8: | Línea 8: | ||
== [[ Mezcla de agua y hielo ]]== | == [[ Mezcla de agua y hielo ]]== | ||
| + | Dentro de un recipiente adiabático se sumerge un bloque de 100 g de hielo a 0.0 °C en 1.0 litros de agua a 20 °C. Determine si se funde todo el hielo y la temperatura final del sistema. ¿Qué ocurre si en lugar de 100 g se tiene 1.0 kg de hielo? | ||
| - | == [[ Mezcla de agua y vapor ]]== | + | ¿Cuánta entropía se produce en cada caso? |
| + | |||
| + | == [[Mezcla de agua y vapor ]]== | ||
| + | En un calorímetro que contiene 200 g de hielo a -8.00<sup>o</sup>C se introducen 50.0 g de vapor de agua a 100<sup>o</sup>C. El equivalente en agua del calorímetro es 20.0 g. Determina el estado final de la mezcla. | ||
| + | |||
| + | Datos: calor específico del hielo: 0.500 cal/g<sup>o</sup>C; entalpía de fusión del hielo: 80.0cal/g; entalpía de vaporización del agua: 537 cal/g | ||
| + | |||
| + | [[Mezcla de agua y vapor|'''Solución''']] | ||
| + | |||
| + | [[Categoría:Problemas del primer principio de la termodinámica]] | ||
== [[ Mezcla de agua y hielo con bloque metálico ]]== | == [[ Mezcla de agua y hielo con bloque metálico ]]== | ||
| + | Un calorímetro contiene 500 g de agua y 300 g de hielo, todo ello a una temperatura de 0°C. Se coge un bloque metálico de 1000 g de un horno cuya temperatura es de 240°C y se deja caer rápidamente dentro del calorímetro, resultando que se produce exactamente la fusión de todo el hielo. ¿Cuál sería la temperatura final del sistema si la masa de hierro fuese el doble? Desprecia las pérdidas caloríficas del calorímetro y su capacidad calorífica. | ||
| + | |||
| + | [[Mezcla de agua y hielo con bloque metálico|'''Solución''' ]] | ||
== [[ Aleación de dos metales ]]== | == [[ Aleación de dos metales ]]== | ||
| - | == [[ Transformación de energía potencial gravitatoria en calor ]]== | + | ==[[Transformación de energía potencial gravitatoria en calor]]== |
| - | Un bloque de hielo a | + | Un bloque de hielo a 0°C se deja caer libremente desde una altura de 80 m. En el momento del choque, un 20% de la energía del bloque se transforma en calor absorbible por su masa. ¿Que parte del hielo se funde a causa de esta absorción? |
| - | un 20% de la energía del bloque se transforma en calor absorbible por su masa. ¿Que parte del hielo se funde a causa de esta absorción? | + | |
| - | [[Solución]] | + | [[Transformación de energía potencial gravitatoria en calor|'''Solución''']] |
| - | == [[ Conducción térmica en dos barras en contacto ]]== | + | ==[[Conducción térmica en dos barras en contacto]]== |
| + | Una barra de oro está en contacto térmico con otra de plata de la misma longitud y área. Uno de los extremos de esta barra compuesta se mantiene a una temperatura de 80°C, mientras que el extremo opuesto está a 30°C. Cuando la transferencia de energía alcance un estado estacionario, ¿cuál será la temperatura en la unión? | ||
| - | + | Datos: conductividad térmica del oro: <math>314\mathrm{W/m\cdot ^oC}</math>; conductividad térmica de la plata: <math>427\mathrm{W/m\cdot ^oC}</math> | |
| - | + | ||
| - | Datos: conductividad térmica del oro: <math>314\mathrm{W/m\cdot ^oC}</math>; | + | |
| - | conductividad térmica de la plata: <math>427\mathrm{W/m\cdot ^oC}</math> | + | |
[[Conducción térmica en dos barras en contacto|'''Solución''']] | [[Conducción térmica en dos barras en contacto|'''Solución''']] | ||
| - | + | == [[Crecimiento de una capa de hielo]]== | |
| - | Un estanque de | + | Un estanque de agua a 0°C está cubierto por una capa de hielo de 4.00°cm de espesor. Si la temperatura del aire permanece constante a |
| - | agua a | + | -10.0°C, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm? |
| - | + | ||
| - | está cubierto | + | |
| - | por una capa | + | |
| - | de hielo de | + | |
| - | 4.00 cm de | + | |
| - | espesor. Si la temperatura del aire | + | |
| - | permanece constante a | + | |
| - | -10.0 | + | |
| - | tardará el espesor de la capa de hielo en | + | |
| - | alcanzar los 8.00 cm? | + | |
[[Crecimiento de una capa de hielo|'''Solución''']] | [[Crecimiento de una capa de hielo|'''Solución''']] | ||
| - | + | == [[ Potencia radiada por el Sol ]]== | |
| + | |||
La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a <math>6.96\times10^8\,\mathrm{m}</math>. | La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a <math>6.96\times10^8\,\mathrm{m}</math>. | ||
Calcule la energía total radiada por el Sol cada segundo si la emisividad es <math>e=0.965</math>. Calcule la potencia que llega a la superficie | Calcule la energía total radiada por el Sol cada segundo si la emisividad es <math>e=0.965</math>. Calcule la potencia que llega a la superficie | ||
| Línea 54: | Línea 55: | ||
[[Potencia radiada por el Sol|'''Solución''']] | [[Potencia radiada por el Sol|'''Solución''']] | ||
| + | |||
| + | [[Categoría:Problemas del primer principio de la termodinámica|0]] | ||
| + | [[Categoría:Primer principio de la termodinámica]] | ||
última version al 11:08 22 feb 2014
1 Trabajo en diferentes procesos
2 Calorímetro de flujo
3 Temperatura de una llama
4 Temperatura de un vaso metálico
5 Mezcla de agua y hielo
Dentro de un recipiente adiabático se sumerge un bloque de 100 g de hielo a 0.0 °C en 1.0 litros de agua a 20 °C. Determine si se funde todo el hielo y la temperatura final del sistema. ¿Qué ocurre si en lugar de 100 g se tiene 1.0 kg de hielo?
¿Cuánta entropía se produce en cada caso?
6 Mezcla de agua y vapor
En un calorímetro que contiene 200 g de hielo a -8.00oC se introducen 50.0 g de vapor de agua a 100oC. El equivalente en agua del calorímetro es 20.0 g. Determina el estado final de la mezcla.
Datos: calor específico del hielo: 0.500 cal/goC; entalpía de fusión del hielo: 80.0cal/g; entalpía de vaporización del agua: 537 cal/g
7 Mezcla de agua y hielo con bloque metálico
Un calorímetro contiene 500 g de agua y 300 g de hielo, todo ello a una temperatura de 0°C. Se coge un bloque metálico de 1000 g de un horno cuya temperatura es de 240°C y se deja caer rápidamente dentro del calorímetro, resultando que se produce exactamente la fusión de todo el hielo. ¿Cuál sería la temperatura final del sistema si la masa de hierro fuese el doble? Desprecia las pérdidas caloríficas del calorímetro y su capacidad calorífica.
8 Aleación de dos metales
9 Transformación de energía potencial gravitatoria en calor
Un bloque de hielo a 0°C se deja caer libremente desde una altura de 80 m. En el momento del choque, un 20% de la energía del bloque se transforma en calor absorbible por su masa. ¿Que parte del hielo se funde a causa de esta absorción?
10 Conducción térmica en dos barras en contacto
Una barra de oro está en contacto térmico con otra de plata de la misma longitud y área. Uno de los extremos de esta barra compuesta se mantiene a una temperatura de 80°C, mientras que el extremo opuesto está a 30°C. Cuando la transferencia de energía alcance un estado estacionario, ¿cuál será la temperatura en la unión?
Datos: conductividad térmica del oro: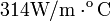 
; conductividad térmica de la plata: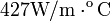 
11 Crecimiento de una capa de hielo
Un estanque de agua a 0°C está cubierto por una capa de hielo de 4.00°cm de espesor. Si la temperatura del aire permanece constante a -10.0°C, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm?
12 Potencia radiada por el Sol
La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a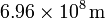 
.
Calcule la energía total radiada por el Sol cada segundo si la emisividad es e = 0.965. Calcule la potencia que llega a la superficie
de la Tierra, si el radio de esta es 
, y la distancia media Tierra-Sol es
.
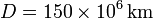