Cómo se hace una integral
De Laplace
(Diferencias entre revisiones)
(→Idea general) |
(→Idea general) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Idea general== | ==Idea general== | ||
| - | A la hora de enfrentarse a una integral (de camino, superficie o volumen, escalar o vectorial) | + | A la hora de enfrentarse a una integral (de camino, superficie o volumen, escalar o vectorial) lo esencial es tener clara la secuencia de pasos para calcularla y no intentar hacerlo todo de una vez. Una estrategia más o menos detallada sería: |
| - | * | + | *Escribir la expresión vectorial de la integral (posiblemente a partir de una idea de que hay que sumar una serie de contribuciones). |
| - | + | *Elegir un sistema de coordenadas adecuado (para esto, las [[Elección de ejes. Simetría|simetrías]] y las [[Líneas y superficies coordenadas|líneas y superficies]] implicadas son esenciales). | |
| - | * | + | *Desarrollar ''al pie de la letra'' lo que indica la expresión de la integral, respectando qué es un escalar y qué es un vector, qué es un producto escalar o de otro tipo, incluyendo los vectores de las bases necesarios,... |
| - | + | *Distinguir qué variables son de integración y cuáles funcionan como parámetros constantes. Por ejemplo en la integral | |
| - | == | + | <center><math>F(x) = \int_a^b (x'-x)^2 dx' = \frac{(b-x)^3-(a-x)^3}{3}</math></center> |
| - | + | :<math>x'\,</math> es la variable de integración y '''no''' aparece en el resultado final, mientras que <math>x\,</math> es un parámetro que, a la hora de integrar, actúa como una constante y sí aparece en el resultado final. | |
| + | |||
| + | *Tener cuidado con cuáles de los términos que aparecen en el integrando dependen de las variables de integración, ya que no siempre se indica explícitamente la dependencia. En particular, recuérdese que, en general: | ||
| + | |||
| + | {{dependen}} | ||
| + | |||
| + | :razón por la cual, en general será preferible el uso de la base cartesiana, ya que | ||
| + | |||
| + | {{basecartesiana}} | ||
| + | |||
| + | |||
| + | *Una vez reducida la integral inicial a una o varias (si es un vector o una integral múltiple) integrales más sencillas, calcular éstas (si es posible, lo cual no ocurre siempre, ni mucho menos). | ||
| + | |||
| + | Para ilustrar estas ideas, varios ejemplos: | ||
| + | |||
| + | * [[Integrales de camino. Ejemplos]] | ||
| + | |||
| + | * [[Integrales de superficie. Ejemplos]] | ||
==Enlaces== | ==Enlaces== | ||
| - | * '''Siguiente:''' | + | * '''Siguiente:''' |
* '''Anterior:''' [[Coordenadas esféricas. Diferenciales]] | * '''Anterior:''' [[Coordenadas esféricas. Diferenciales]] | ||
[[Categoría:Diferenciales|50]] | [[Categoría:Diferenciales|50]] | ||
última version al 11:36 24 nov 2007
1 Idea general
A la hora de enfrentarse a una integral (de camino, superficie o volumen, escalar o vectorial) lo esencial es tener clara la secuencia de pasos para calcularla y no intentar hacerlo todo de una vez. Una estrategia más o menos detallada sería:
- Escribir la expresión vectorial de la integral (posiblemente a partir de una idea de que hay que sumar una serie de contribuciones).
- Elegir un sistema de coordenadas adecuado (para esto, las simetrías y las líneas y superficies implicadas son esenciales).
- Desarrollar al pie de la letra lo que indica la expresión de la integral, respectando qué es un escalar y qué es un vector, qué es un producto escalar o de otro tipo, incluyendo los vectores de las bases necesarios,...
- Distinguir qué variables son de integración y cuáles funcionan como parámetros constantes. Por ejemplo en la integral
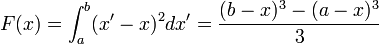
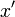es la variable de integración y no aparece en el resultado final, mientras que 
es un parámetro que, a la hora de integrar, actúa como una constante y sí aparece en el resultado final.
- Tener cuidado con cuáles de los términos que aparecen en el integrando dependen de las variables de integración, ya que no siempre se indica explícitamente la dependencia. En particular, recuérdese que, en general:
Los vectores de la base dependen de la posición
- razón por la cual, en general será preferible el uso de la base cartesiana, ya que
La base cartesiana es la única independiente de la posición
- Una vez reducida la integral inicial a una o varias (si es un vector o una integral múltiple) integrales más sencillas, calcular éstas (si es posible, lo cual no ocurre siempre, ni mucho menos).
Para ilustrar estas ideas, varios ejemplos:
2 Enlaces
- Siguiente:
- Anterior: Coordenadas esféricas. Diferenciales
