Integrales de superficie. Ejemplos

De Laplace

Contenido

1 Enunciado
2 Primera integral
3 Segunda integral
4 Enlaces

1 Enunciado

Imaginemos que se nos pide calcular las dos integrales siguientes

$\oint \mathbf{A}\cdot\mathrm{d}\mathbf{S}\qquad\qquad \oint\mathbf{A}\,\mathrm{d}S$

donde

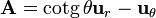
$\mathbf{A} =\mathrm{cotg}\,\theta\mathbf{u}_{r}-\mathbf{u}_{\theta}$

y la superficie de integración es una esfera de radio $R$ con centro el origen de coordenadas.

Si no estamos atentos, podemos preguntarnos, ¿no son acaso la misma integral? ¿Qué diferencia hay entre ellas?

Con un poco de atención podemos ver que

En la primera integral 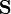$\mathbf{S}$ aparece en negrita, mientras que en la segunda aparece en cursiva, $S$ , lo cual quiere decir que en el primer caso se trata de un vector mientras que en el segundo se trata de un escalar.

Para reforzar lo anterior, podemos ver que en la integral de la izquierda hay un puntito, que indica que se trata de un producto escalar, el cual no sería aplicable si se tratara de escalares

Por tanto, en la primera integral el resultado es un número, mientras que en la segunda se trata de un vector.

Veamos cada integral por separado:

2 Primera integral

2.1 Enunciado

En el primer caso, se trata de hallar

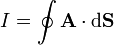
$I = \oint \mathbf{A}\cdot\mathrm{d}\mathbf{S}$

donde

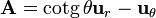
$\mathbf{A} =\mathrm{cotg}\,\theta\mathbf{u}_{r}-\mathbf{u}_{\theta}$

y la superficie de integración es una esfera de radio $R$ con centro el origen de coordenadas.

El resultado de esta integral es un número. Resulta de sumar todos los productos escalares 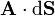$\mathbf{A}\cdot\mathrm{d}\mathbf{S}$ .

2.2 Elección de coordenadas

Puesto que la superficie de integración es una esfera, es natural emplear coordenadas esféricas. En éstas, la superficie de integración es

$r = R\qquad \theta\in [0,\pi]\qquad\varphi \in [0,2\pi)$

y el diferencial de superficie correspondiente

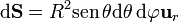
$\mathrm{d}\mathbf{S} = R^2 \mathrm{sen}\,\theta\mathrm{d}\theta\,\mathrm{d}\varphi\mathbf{u}_r$

La función vectorial a integrar ya está en coordenadas esféricas, así que no hay que tocarla.

El producto escalar vale

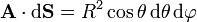
$\mathbf{A}\cdot\mathrm{d}\mathbf{S} = R^2\cos\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi$

2.3 Cálculo de la integral

Sustituyendo lo anterior

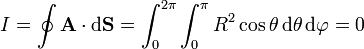
$I = \oint \mathbf{A}\cdot\mathrm{d}\mathbf{S}=\int_0^{2\pi}\int_0^\pi R^2\cos\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi = 0$

ya que la integral del coseno entre 0 y π es nula.

3 Segunda integral

3.1 Enunciado

En el segundo caso, se trata de hallar

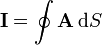
$\mathbf{I} = \oint \mathbf{A}\,\mathrm{d}S$

donde

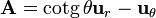
$\mathbf{A} =\mathrm{cotg}\,\theta\mathbf{u}_{r}-\mathbf{u}_{\theta}$

y la superficie de integración es una esfera de radio $R$ con centro el origen de coordenadas.

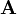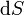Como dijimos antes, el resultado de esta integral es un vector. Resulta de sumar todos los productos de los vectores $\mathbf{A}\,$ por los escalares $\mathrm{d}S\,$ .

3.2 Elección de coordenadas

Como en el ejemplo anterior, lo natural es emplear coordenadas esféricas. En éstas, la superficie de integración es

$r = R\qquad \theta\in [0,\pi]\qquad\varphi \in [0,2\pi)$

y el diferencial de superficie escalar correspondiente

$\mathrm{d}S = R^2 \mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi$

El diferencial escalar consiste solamente en el área de un elemento de superficie. Por tanto, no incorpora el vector 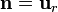$\mathbf{n}=\mathbf{u}_r$ .

La función vectorial a integrar ya está en coordenadas esféricas, así que no hay que tocarla.

El producto 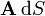$\mathbf{A}\,\mathrm{d}S$ vale

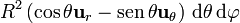
$R^2\left(\cos\theta\mathbf{u}_{r}-\mathrm{sen} \,\theta\mathbf{u}_{\theta}\right)\,\mathrm{d}\theta\,\mathrm{d}\varphi$

3.3 Cálculo de la integral

Sustituyendo lo anterior

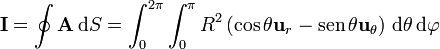
$\mathbf{I} = \oint \mathbf{A}\,\mathrm{d}S=\int_0^{2\pi}\int_0^\pi R^2\left(\cos\theta\mathbf{u}_{r}-\mathrm{sen} \,\theta\mathbf{u}_{\theta}\right)\,\mathrm{d}\theta\,\mathrm{d}\varphi$

Ahora la tentación es considerar que esto es igual a

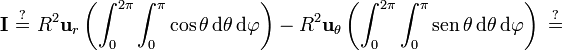
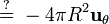
$\mathbf{I}\ \stackrel{?}{=}\ R^2\mathbf{u}_r\left(\int_0^{2\pi}\int_0^\pi \cos\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\right)-R^2\mathbf{u}_\theta\left( \int_0^{2\pi}\int_0^\pi \mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\right)\ \stackrel{?}{=}$ $\stackrel{?}{=}\ -4\pi R^2\mathbf{u}_\theta$

pero esto es falso, ya que no tiene en cuenta que

Los vectores de la base dependen de la posición

y por tanto deben ser tenidos en cuenta a la hora de integrar. Empleando las relaciones entre las bases vectoriales queda

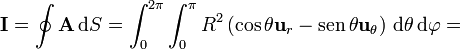
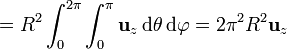
$\mathbf{I} = \oint \mathbf{A}\,\mathrm{d}S=\int_0^{2\pi}\int_0^\pi R^2\left(\cos\theta\mathbf{u}_{r}-\mathrm{sen} \,\theta\mathbf{u}_{\theta}\right)\,\mathrm{d}\theta\,\mathrm{d}\varphi =$ $= R^2\int_0^{2\pi}\int_0^\pi \mathbf{u}_z\,\mathrm{d}\theta\,\mathrm{d}\varphi = 2\pi^2R^2\mathbf{u}_z$

Una forma de ver que el resultado anterior era incorrecto es observando que el vector 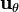$\mathbf{u}_\theta$ sólo tiene sentido cuando se aplica a un punto en concreto, pero no cuando se habla de la esfera como un todo. Si 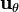$\mathbf{u}_\theta$ tiene una dirección diferente en cada punto, ¿hacia donde apunta cuando lo aplicamos a la suma sobre una esfera? Por ello, es importante pasar a la base cartesiana ya que

La base cartesiana es la única independiente de la posición

4 Enlaces

Siguiente: Campos escalares y vectoriales

Integrales de superficie. Ejemplos

De Laplace

Contenido

1 Enunciado

2 Primera integral

2.1 Enunciado

2.2 Elección de coordenadas

2.3 Cálculo de la integral

3 Segunda integral

3.1 Enunciado

3.2 Elección de coordenadas

3.3 Cálculo de la integral

4 Enlaces

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES