Problemas de cinética (CMR)
De Laplace
(→Tres masas en un triángulo) |
(→Cinética de un cono) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 34: | Línea 34: | ||
[[Sistema de dos masas unidas por una varilla (CMR)|'''Solución''']] | [[Sistema de dos masas unidas por una varilla (CMR)|'''Solución''']] | ||
| + | |||
| + | ==Cinética de un cono== | ||
| + | Se tiene un cono homogéneo, de radio de la base R, altura H y masa m distribuida uniformemente. | ||
| + | # Localice la posición del centro de masas del cono empleando un sistema de ejes en el que el cono tiene su vértice en el origen de coordenadas y el eje del cono es el OZ. | ||
| + | # Calcule los momentos de inercia respecto al eje del cono, OZ, y los ejes ortogonales OY y OX | ||
| + | # Halle el momento de inercia respecto a dos ejes, paralelos a OX y OY por el centro de masas. | ||
| + | # Supongamos que el cono se hace girar con velocidad angular constante Ω alrededor de una generatriz, que se toma como eje <math>OZ_2</math>. | ||
| + | ## ¿Cuánto vale su momento cinético respecto al vértice del cono, O? | ||
| + | ## ¿Cuánto vale su energía cinética? | ||
| + | ## Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen? | ||
| + | <center>[[Archivo:cono-solido-ejes.png|200px]]</center> | ||
| + | |||
| + | [[Cinética de un cono (CMR)|'''Solucion''']] | ||
última version al 10:07 12 ene 2021
Contenido |
1 Tres masas en un triángulo
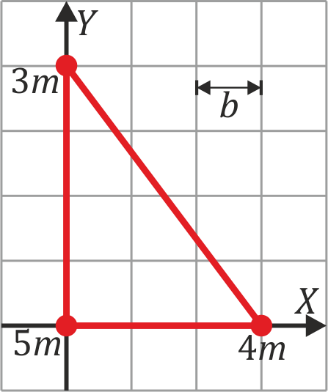
Un sólido rígido está formado por tres masas: una 5m, situada en O(0,0,0), una 4m, en A(3b,0,0) y una 3m, en B(0,4b,0).
- ¿En qué posición se encuentra el centro de masas del sistema?
- ¿Cuánto vale el tensor de inercia de este sólido respecto a unos ejes paralelos a OX, OY y OZ, por el centro de masas?
- Si el sólido está girando en torno a un eje que pasa por el CM y con velocidad angular
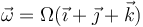 , calcule cuánto valen
, calcule cuánto valen
- su momento cinético respecto a G.
- su momento cinético respecto a O.
- su energía cinética.
2 Momento de inercia de sólidos esféricos
Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.
A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R1 y exterior R2 respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?
3 Tensor de inercia de esfera hueca
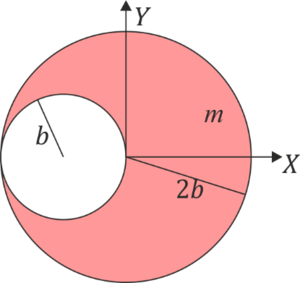
Sea un sólido en forma de esfera maciza de radio 2b en la que se ha hecho una cavidad también esférica de radio b. La masa total del sólido es m. Determine el tensor de inercia de este sólido respecto al sistema de referencia de la figura.
4 Sistema de dos masas unidas por una varilla
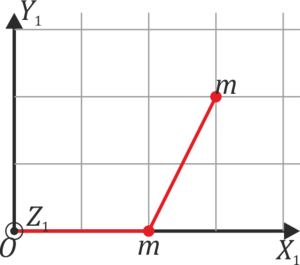
Un sólido está formado por dos masas iguales,m1 = m2 = m, unidas por una varilla sin masa. En un instante dado, las dos partículas se hallan en 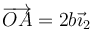 y
y 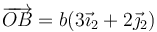 , respectivamente, siendo el sistema OX2Y2Z2 uno ligado al sólido (OX1Y1Z1 sería un sistema fijo).
, respectivamente, siendo el sistema OX2Y2Z2 uno ligado al sólido (OX1Y1Z1 sería un sistema fijo).
- ¿Cuál es la posición del CM del sistema?
- ¿Cuánto vale su tensor de inercia respecto al triedro OX2Y2Z2?
- Determine los ejes principales de inercia y los momentos principales de inercia de este sólido.
- Si la varilla gira con velocidad angular constante
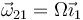 alrededor del eje OX1 = OX2, ¿cuánto vale su momento cinético respecto a O? ¿Y su energía cinética?
alrededor del eje OX1 = OX2, ¿cuánto vale su momento cinético respecto a O? ¿Y su energía cinética?
- Para el movimiento anterior, ¿qué fuerza y que momento hay que aplicar en O para mantener el sistema en movimiento?
5 Cinética de un cono
Se tiene un cono homogéneo, de radio de la base R, altura H y masa m distribuida uniformemente.
- Localice la posición del centro de masas del cono empleando un sistema de ejes en el que el cono tiene su vértice en el origen de coordenadas y el eje del cono es el OZ.
- Calcule los momentos de inercia respecto al eje del cono, OZ, y los ejes ortogonales OY y OX
- Halle el momento de inercia respecto a dos ejes, paralelos a OX y OY por el centro de masas.
- Supongamos que el cono se hace girar con velocidad angular constante Ω alrededor de una generatriz, que se toma como eje OZ2.
- ¿Cuánto vale su momento cinético respecto al vértice del cono, O?
- ¿Cuánto vale su energía cinética?
- Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen?






