Sistema de dos masas unidas por una varilla (CMR)

De Laplace

Contenido

1 Enunciado
2 Centro de masas
3 Tensor de inercia
4 Ejes y momentos principales
5 Momento y energía cinética
- 5.1 Momento cinético
- 5.2 Energía cinética
6 Fuerza y par
- 6.1 Fuerza
- 6.2 Momento de las fuerzas

1 Enunciado

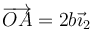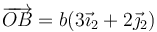Un sólido está formado por dos masas iguales, $m 1 = m 2 = m$ , unidas por una varilla sin masa. En un instante dado, las dos partículas se hallan en $\overrightarrow{OA}=2b\vec{\imath}_2$ y $\overrightarrow{OB}=b(3\vec{\imath}_2+2\vec{\jmath}_2 )$ , respectivamente, siendo el sistema $O X 2 Y 2 Z 2$ uno ligado al sólido ( $O X 1 Y 1 Z 1$ sería un sistema fijo).

¿Cuál es la posición del CM del sistema?
¿Cuánto vale su tensor de inercia respecto al triedro $O X 2 Y 2 Z 2$ ?
Determine los ejes principales de inercia y los momentos principales de inercia de este sólido.
Si la varilla gira con velocidad angular constante 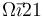$\Omega\vec{\imath}21$ alrededor del eje $O X 1 = O X 2$ , ¿cuánto vale su momento cinético respecto a O? ¿Y su energía cinética?
Para el movimiento anterior, ¿qué fuerza y que momento hay que aplicar en O para mantener el sistema en movimiento?

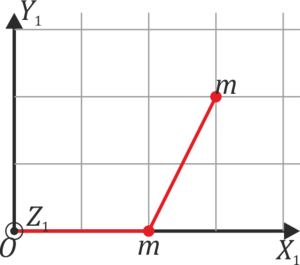
2 Centro de masas

Al ser las dos masas iguales, el centro de masas se halla en el punto medio

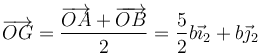
$\overrightarrow{OG}=\frac{\overrightarrow{OA}+\overrightarrow{OB}}{2}=\frac{5}{2}b\vec{\imath}_2+b\vec{\jmath}_2$

3 Tensor de inercia

Para un sistema de masas puntuales, basta con sumar las contribuciones de cada una a los diferentes momentos y productos de inercia.

3.1 Respecto al eje OX

La masa 1 se halla sobre el propio eje y la 2 a una distancia 2b, por tanto

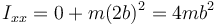
$I_{xx}=0+m(2b)^2=4mb^2\,$

3.2 Respecto al eje OY

La masa 1 está a 2b y la 2 a 3b

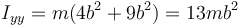
$I_{yy}=m(4b^2+9b^2)=13mb^2\,$

3.3 Respecto al eje OZ

Se trata de una figura plana en el plano $O X 1 Y 1$ por lo que

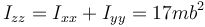
$I_{zz}=I_{xx}+I_{yy}=17mb^2\,$

3.4 Productos de inercia

Por ser una figura plana en $O X 1 Y 1$

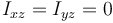
$I_{xz}=I_{yz}=0\,$

El único elemento no diagonal no nulo es el xy

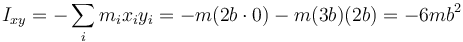
$I_{xy}=-\sum_i m_i x_iy_i=-m(2b\cdot 0)-m(3b)(2b)=-6mb^2\,$

3.5 Forma matricial

Reuniendo los resultados anteriores queda la matriz

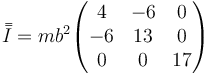
$\bar{\bar{I}}=mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17\end{pmatrix}$

También se puede calcular esta matriz directamente en lugar de elemento a elemento, partiendo de la expresión

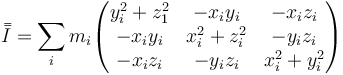
$\bar{\bar{I}}=\sum_i m_i\begin{pmatrix} y_i^2+z_1^2 & -x_iy_i & -x_iz_i \\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2+y_i^2 \end{pmatrix}$

que en este caso nos da

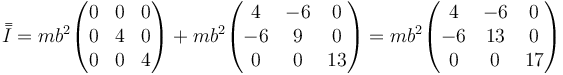
$\bar{\bar{I}}=mb^2\begin{pmatrix} 0 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end{pmatrix}+mb^2\begin{pmatrix} 4 & -6 & 0 \\ -6 & 9 & 0 \\ 0 & 0 & 13 \end{pmatrix}=mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17\end{pmatrix}$

4 Ejes y momentos principales

Los momentos principales de inercia resultan de resolver el determinante

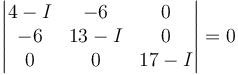
$\left|\begin{matrix}4-I & -6 & 0 \\ -6 & 13-I & 0 \\ 0 & 0 & 17-I \end{matrix}\right|=0$

(donde en el resultado final habrá que multiplicar el número que salga por $m b 2$ ). Desarrollamos el determinante

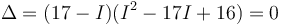
$\Delta = (17-I)(I^2-17I+16)=0\,$

Uno de los autovalores es inmediato, $I Z Z = 17 m b 2$ . Esto era de esperar pues ya sabíamos que el eje OZ era principal. Los otros dos salen de una ecuación de segundo grado

$I_{XX}=mb^2 \qquad\qquad I_{YY}=16mb^2$

Para hallar cada autovector resolvemos la ecuación vectorial. Para $I Z Z$ es inmediato

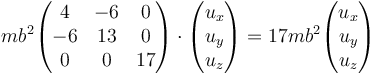
$mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17 \end{pmatrix}\cdot\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}=17mb^2\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}$

que da el sistema

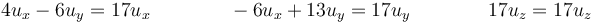
$4u_x-6u_y=17u_x\qquad\qquad -6u_x+13u_y=17u_y \qquad\qquad 17u_z=17u_z$

con solución

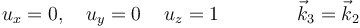
$u_x=0,\quad u_y=0\,\quad u_z=1\qquad\qquad\vec{k}_3=\vec{k}_2$

Para el autovalor $I X X$ operamos de la misma forma

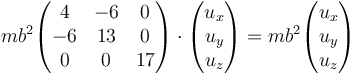
$mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17 \end{pmatrix}\cdot\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}=mb^2\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}$

que da el sistema

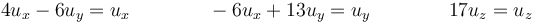
$4u_x-6u_y=u_x\qquad\qquad -6u_x+13u_y=u_y \qquad\qquad 17u_z=u_z$

con solución

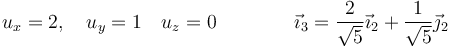
$u_x=2,\quad u_y=1\quad u_z=0\qquad\qquad\vec{\imath}_3=\frac{2}{\sqrt{5}}\vec{\imath}_2+\frac{1}{\sqrt{5}}\vec{\jmath}_2$

donde en el última paso se ha normalizado el vector.

Por último, para el autovalor $I Y Y = 16 m b 2$ resulta el tercer vector del triedro

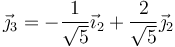
$\vec{\jmath}_3=-\frac{1}{\sqrt{5}}\vec{\imath}_2+\frac{2}{\sqrt{5}}\vec{\jmath}_2$

En esta base, el tensor de inercia se escribe

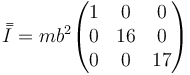
$\bar{\bar{I}}=mb^2\begin{pmatrix}1 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 17 \end{pmatrix}$

5 Momento y energía cinética

5.1 Momento cinético

Para el momento cinético no necesitamos los momentos o ejes principales (aunque en problemas de dinámica donde haya que resolver las ecuaciones de Euler si son muy útiles). Nos basta con multiplicar el tensor de inercia por la velocidad angular

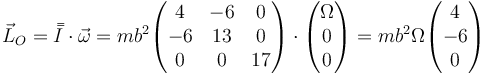
$\vec{L}_O=\bar{\bar{I}}\cdot\vec{\omega}=mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17\end{pmatrix}\cdot\begin{pmatrix}\Omega \\ 0 \\ 0 \end{pmatrix}=mb^2\Omega\begin{pmatrix}4 \\ -6 \\ 0 \end{pmatrix}$

o, en forma vectorial,

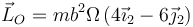
$\vec{L}_O=mb^2\Omega\left(4\vec{\imath}_2-6\vec{\jmath}_2\right)$

Por no ser $O X 2$ un eje principal, el momento cinético no es paralelo a la velocidad angular.

Nótese que el momento cinético es constante en el sistema de referencia 2, ligado al sólido, pero no en el 1, fijo. A medida que el sólido gira, el vector momento cinético lo acompaña, describiendo un cono.

5.2 Energía cinética

Conocido el momento cinético, la energía cinética se calcula como

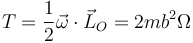
$T=\frac{1}{2}\vec{\omega}\cdot\vec{L}_O=2mb^2\Omega$

Aquí es importante el hecho de que O es un punto fijo respecto a este movimiento. Si no fuera así la expresión sería más complicada.

6 Fuerza y par

6.1 Fuerza

Por la ley de Newton

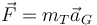
$\vec{F}=m_T\vec{a}_G$

aquí $m T$ es la masa total

$m_T=2m\,$

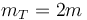
y 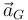$\vec{a}_G$ es la aceleración del CM respecto a un sistema fijo.

El CM está describiendo un movimiento circular uniforme de radio $b$ , por lo que su aceleración es puramente normal, dirigida hacia el eje de rotación (el OX)

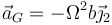
$\vec{a}_G=-\Omega^2 b\vec{\jmath}_2$

y

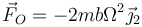
$\vec{F}_O=-2mb\Omega^2\vec{\jmath}_2$

De manera más formal y general, podemos introducir la velocidad angular relativa entre los dos sólidos (que no será otra que la de rotación)

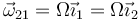
$\vec{\omega}_{21}=\Omega\vec{\imath}_1=\Omega\vec{\imath}_2$

El centro de masas está estacionario respecto al sistema de referencia 2. Por ello, su aceleración es

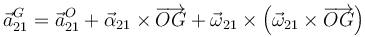
$\vec{a}^G_{21}=\vec{a}^O_{21}+\vec{\alpha}_{21}\times \overrightarrow{OG}+\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{OG}\right)$

El punto O es fijo, por lo que su aceleración es nula. También se anula la aceleración angular, por lo que nos queda

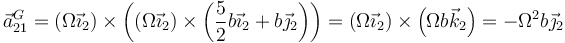
$\vec{a}^G_{21}=(\Omega\vec{\imath}_2)\times \left((\Omega\vec{\imath}_2) \times \left(\frac{5}{2}b\vec{\imath}_2+b\vec{\jmath}_2\right)\right)=(\Omega\vec{\imath}_2)\times \left(\Omega b\vec{k}_2\right)=-\Omega^2b\vec{\jmath}_2$

y de aquí llegamos a la fuerza

$\vec{F}_O=-2mb\Omega^2\vec{\jmath}_2$

Nótese que, de nuevo, esta fuerza es constante en el sistema 2, pero en un sistema fijo la dirección de la fuerza va girando.

6.2 Momento de las fuerzas

Por ser O un punto fijo

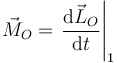
$\vec{M}_O=\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1$

En este caso, el momento cinético acompaña al sólido en su rotación, de forma que en el sistema 2 es constante

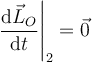
$\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_2=\vec{0}$

por lo que, según la fórmula de Poisson

$\vec{M}_O=\overbrace{\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_2}^{=\vec{0}}+\vec{\omega}_{21}\times\vec{L}_O=(\Omega\vec{\imath}_1)\times \left(mb^2\Omega\left(4\vec{\imath}_1-6\vec{\jmath}_1\right)\right)=-6mb^2\Omega\vec{k}_1$

Sistema de dos masas unidas por una varilla (CMR)

De Laplace

Contenido

1 Enunciado

2 Centro de masas

3 Tensor de inercia

3.1 Respecto al eje OX

3.2 Respecto al eje OY

3.3 Respecto al eje OZ

3.4 Productos de inercia

3.5 Forma matricial

4 Ejes y momentos principales

5 Momento y energía cinética

5.1 Momento cinético

5.2 Energía cinética

6 Fuerza y par

6.1 Fuerza

6.2 Momento de las fuerzas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES