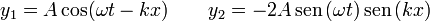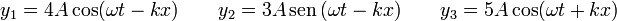Problemas de Movimiento ondulatorio
De Laplace
(→Tensión de una cuerda de piano) |
(→Características de una onda en una cuerda) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==[[Pulso en una cuerda]]== |
Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma | Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma | ||
| Línea 10: | Línea 10: | ||
# Calcule la velocidad del punto de la cuerda situado en ''x'' = 15 cm, en (a) ''t'' = 0 s, (b) ''t'' = 0.5 s, (c) ''t'' = 1 s. | # Calcule la velocidad del punto de la cuerda situado en ''x'' = 15 cm, en (a) ''t'' = 0 s, (b) ''t'' = 0.5 s, (c) ''t'' = 1 s. | ||
| - | + | [[Pulso en una cuerda|'''Solución''']] | |
| + | |||
| + | ==[[Propiedades de una onda sinusoidal]]== | ||
Una perturbación a lo largo de una cuerda se describe mediante la ecuación | Una perturbación a lo largo de una cuerda se describe mediante la ecuación | ||
| Línea 21: | Línea 23: | ||
[[Propiedades de una onda sinusoidal|'''Solución''']] | [[Propiedades de una onda sinusoidal|'''Solución''']] | ||
| - | + | ==[[Solución de onda estacionaria]]== | |
Una perturbación de una cuerda es de la forma | Una perturbación de una cuerda es de la forma | ||
| Línea 31: | Línea 33: | ||
[[Solución de onda estacionaria|'''Solución''']] | [[Solución de onda estacionaria|'''Solución''']] | ||
| - | + | ==[[Propiedades de una onda]]== | |
Una onda sinusoidal transversal que se desplaza por una cuerda tiene un periodo ''T'' = 25.0 ms y viaja en la dirección negativa | Una onda sinusoidal transversal que se desplaza por una cuerda tiene un periodo ''T'' = 25.0 ms y viaja en la dirección negativa | ||
del eje ''x'' a una velocidad de 30 m/s. En el instante ''t'' = 0 s una partícula de la cuerda situada en la posición ''x'' = 0 m tiene un desplazamiento de 2.00 cm y se mueve hacia abajo con una velocidad de 2 m/s. Halle la amplitud, la longitud de onda, y el desfase inicial de esta señal. | del eje ''x'' a una velocidad de 30 m/s. En el instante ''t'' = 0 s una partícula de la cuerda situada en la posición ''x'' = 0 m tiene un desplazamiento de 2.00 cm y se mueve hacia abajo con una velocidad de 2 m/s. Halle la amplitud, la longitud de onda, y el desfase inicial de esta señal. | ||
| Línea 37: | Línea 39: | ||
[[Propiedades de una onda|'''Solución''']] | [[Propiedades de una onda|'''Solución''']] | ||
| - | + | ==Características de una onda en una cuerda== | |
| - | Una cuerda de masa 0. | + | Una cuerda de masa 0.200 kg y 4.00 m de longitud se conecta a un diapasón que oscila con una frecuencia de 20.0 Hz. La amplitud de las oscilaciones es de 1.00 cm. La onda transversal excitada en la cuerda resulta tener una longitud de onda de 10.0 cm. Determine la velocidad de la onda y la tensión aplicada a la cuerda. ¿Por qué factor es preciso multiplicar la tensión aplicada para que la longitud de onda se duplique? |
| - | + | ==[[Onda en un hilo bimetálico]]== | |
Un hilo de acero (ρ = 7.85 g/cm³) de 3.0 m y un hilo de cobre (ρ = 8.96 g/cm³) de 2.0 m ambos con un diámetro de 1 mm están conectados por un extremo. El extremo libre del acero está atado al techo, mientras que del del cobre cuelga una masa de 20 kg. ¿Cuánto tarda una oscilación de la masa en llegar hasta el techo? | Un hilo de acero (ρ = 7.85 g/cm³) de 3.0 m y un hilo de cobre (ρ = 8.96 g/cm³) de 2.0 m ambos con un diámetro de 1 mm están conectados por un extremo. El extremo libre del acero está atado al techo, mientras que del del cobre cuelga una masa de 20 kg. ¿Cuánto tarda una oscilación de la masa en llegar hasta el techo? | ||
| Línea 47: | Línea 49: | ||
[[Onda en un hilo bimetálico|'''Solución''']] | [[Onda en un hilo bimetálico|'''Solución''']] | ||
| - | + | ==Potencia en una cuerda vibrante== | |
Se van a transmitir ondas sinusoidales de 5.00 cm de amplitud a lo largo de una cuerda que tiene una densidad de masa lineal 40 g/m. Si la fuente puede proporcionar una potencia máxima de 300 W y la cuerda soporta una tensión de 300 N ¿cuál es la frecuencia de vibración más alta con que puede operar la fuente? | Se van a transmitir ondas sinusoidales de 5.00 cm de amplitud a lo largo de una cuerda que tiene una densidad de masa lineal 40 g/m. Si la fuente puede proporcionar una potencia máxima de 300 W y la cuerda soporta una tensión de 300 N ¿cuál es la frecuencia de vibración más alta con que puede operar la fuente? | ||
| - | + | ==Potencia en una onda estacionaria== | |
Dos ondas sinusoidales de la misma amplitud y frecuencia viajan por una cuerda tensa en direcciones opuestas. Calcule y dibuje la forma de la onda resultante. Demuestre que la potencia promedio transmitida por esta onda es nula. | Dos ondas sinusoidales de la misma amplitud y frecuencia viajan por una cuerda tensa en direcciones opuestas. Calcule y dibuje la forma de la onda resultante. Demuestre que la potencia promedio transmitida por esta onda es nula. | ||
| - | + | ==[[Superposición de dos y tres señales]]== | |
Considere los casos de superposición siguientes | Considere los casos de superposición siguientes | ||
| Línea 65: | Línea 67: | ||
[[Superposición de dos y tres señales|'''Solución''']] | [[Superposición de dos y tres señales|'''Solución''']] | ||
| - | + | ==[[Tensión de una cuerda de piano]]== | |
Las cuerdas de los pianos están hechas esencialmente de acero (ρ = 7.85 g/cm³) tensado | Las cuerdas de los pianos están hechas esencialmente de acero (ρ = 7.85 g/cm³) tensado | ||
| - | # Determine la ecuación para la tensión de una cuerda si su diámetro es '' | + | # Determine la ecuación para la tensión de una cuerda si su diámetro es ''D'' y su longitud ''L'' y debe producir una nota de frecuencia ''f''. |
| - | # La nota más grave de un piano es el La de la subcontraoctava (27.5 Hz). Calcule la longitud que debería tener esta cuerda si está hecha de hilo de 1.224 | + | # La nota más grave de un piano es el La de la subcontraoctava (27.5 Hz). Calcule la longitud que debería tener esta cuerda si está hecha de hilo de 1.224 mm de diámetro y sometida a una tensión de 600 N. ¿Es factible esta longitud? |
# Si la longitud de la cuerda está limitada a 110 cm, ¿con qué tensión habría que tensar el hilo anterior para producir la misma nota? | # Si la longitud de la cuerda está limitada a 110 cm, ¿con qué tensión habría que tensar el hilo anterior para producir la misma nota? | ||
# Si la tensión debe ser 600 N y la longitud 110 cm, ¿qué grosor debería tener la cuerda para producir esta nota? ¿Cuál es el problema de este grosor? | # Si la tensión debe ser 600 N y la longitud 110 cm, ¿qué grosor debería tener la cuerda para producir esta nota? ¿Cuál es el problema de este grosor? | ||
| Línea 76: | Línea 78: | ||
[[Tensión de una cuerda de piano|'''Solución''']] | [[Tensión de una cuerda de piano|'''Solución''']] | ||
| - | + | ==[[Batidos en un piano]]== | |
Para las notas agudas de los pianos se emplean cuerdas dobles o triples, formadas por hilos de acero paralelos. El La de la octava menor (110 Hz) está formado por dos hilos, tensados teóricamente a 600 N. Uno de los dos hilos se destensa ligeramente y al tocar la tecla se oyen batidos con una frecuencia de 4 Hz. ¿Cuál es la tensión de la cuerda destensada? | Para las notas agudas de los pianos se emplean cuerdas dobles o triples, formadas por hilos de acero paralelos. El La de la octava menor (110 Hz) está formado por dos hilos, tensados teóricamente a 600 N. Uno de los dos hilos se destensa ligeramente y al tocar la tecla se oyen batidos con una frecuencia de 4 Hz. ¿Cuál es la tensión de la cuerda destensada? | ||
última version al 12:21 12 ene 2011
1 Pulso en una cuerda
Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma
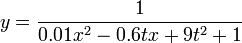
donde x e y se miden en centímetros y t en segundos.
- Halle la velocidad de esta onda.
- Demuestre que esta señal cumple la ecuación de onda.
- Calcule la velocidad del punto de la cuerda situado en x = 15 cm, en (a) t = 0 s, (b) t = 0.5 s, (c) t = 1 s.
2 Propiedades de una onda sinusoidal
Una perturbación a lo largo de una cuerda se describe mediante la ecuación
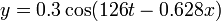
con x e y medidos en centímetros y t en segundos.
Para esta onda, halle su amplitud, frecuencia angular, periodo, número de onda y longitud de onda.
3 Solución de onda estacionaria
Una perturbación de una cuerda es de la forma
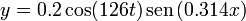
con x e y medidos en centímetros y t en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le corresponde?
4 Propiedades de una onda
Una onda sinusoidal transversal que se desplaza por una cuerda tiene un periodo T = 25.0 ms y viaja en la dirección negativa del eje x a una velocidad de 30 m/s. En el instante t = 0 s una partícula de la cuerda situada en la posición x = 0 m tiene un desplazamiento de 2.00 cm y se mueve hacia abajo con una velocidad de 2 m/s. Halle la amplitud, la longitud de onda, y el desfase inicial de esta señal.
5 Características de una onda en una cuerda
Una cuerda de masa 0.200 kg y 4.00 m de longitud se conecta a un diapasón que oscila con una frecuencia de 20.0 Hz. La amplitud de las oscilaciones es de 1.00 cm. La onda transversal excitada en la cuerda resulta tener una longitud de onda de 10.0 cm. Determine la velocidad de la onda y la tensión aplicada a la cuerda. ¿Por qué factor es preciso multiplicar la tensión aplicada para que la longitud de onda se duplique?
6 Onda en un hilo bimetálico
Un hilo de acero (ρ = 7.85 g/cm³) de 3.0 m y un hilo de cobre (ρ = 8.96 g/cm³) de 2.0 m ambos con un diámetro de 1 mm están conectados por un extremo. El extremo libre del acero está atado al techo, mientras que del del cobre cuelga una masa de 20 kg. ¿Cuánto tarda una oscilación de la masa en llegar hasta el techo?
Suponga despreciable el incremento en la tensión debido al peso de los propios cables. ¿Podría hacerse una estimación del error cometido al hacer esta aproximación?
7 Potencia en una cuerda vibrante
Se van a transmitir ondas sinusoidales de 5.00 cm de amplitud a lo largo de una cuerda que tiene una densidad de masa lineal 40 g/m. Si la fuente puede proporcionar una potencia máxima de 300 W y la cuerda soporta una tensión de 300 N ¿cuál es la frecuencia de vibración más alta con que puede operar la fuente?
8 Potencia en una onda estacionaria
Dos ondas sinusoidales de la misma amplitud y frecuencia viajan por una cuerda tensa en direcciones opuestas. Calcule y dibuje la forma de la onda resultante. Demuestre que la potencia promedio transmitida por esta onda es nula.
9 Superposición de dos y tres señales
Considere los casos de superposición siguientes
Para cada uno de los casos, determine la ecuación de la señal resultante, ¿es una onda viajera o una estacionaria?
10 Tensión de una cuerda de piano
Las cuerdas de los pianos están hechas esencialmente de acero (ρ = 7.85 g/cm³) tensado
- Determine la ecuación para la tensión de una cuerda si su diámetro es D y su longitud L y debe producir una nota de frecuencia f.
- La nota más grave de un piano es el La de la subcontraoctava (27.5 Hz). Calcule la longitud que debería tener esta cuerda si está hecha de hilo de 1.224 mm de diámetro y sometida a una tensión de 600 N. ¿Es factible esta longitud?
- Si la longitud de la cuerda está limitada a 110 cm, ¿con qué tensión habría que tensar el hilo anterior para producir la misma nota?
- Si la tensión debe ser 600 N y la longitud 110 cm, ¿qué grosor debería tener la cuerda para producir esta nota? ¿Cuál es el problema de este grosor?
- Si un piano tiene un total de 200 cuerdas, ¿a qué tensión se encuentra la estructura del piano?
11 Batidos en un piano
Para las notas agudas de los pianos se emplean cuerdas dobles o triples, formadas por hilos de acero paralelos. El La de la octava menor (110 Hz) está formado por dos hilos, tensados teóricamente a 600 N. Uno de los dos hilos se destensa ligeramente y al tocar la tecla se oyen batidos con una frecuencia de 4 Hz. ¿Cuál es la tensión de la cuerda destensada?