Primera Prueba de Control 2018/19 (MR G.I.C.)
De Laplace
(qui) |
(→Barra deslizando sobre esquina) |
||
| Línea 11: | Línea 11: | ||
#Encuentra la reducción cinemática del movimiento {21} en el punto <math>A</math>. ¿Cuál es la velocidad <math>\vec{v}^{\,O}_{21}</math>? | #Encuentra la reducción cinemática del movimiento {21} en el punto <math>A</math>. ¿Cuál es la velocidad <math>\vec{v}^{\,O}_{21}</math>? | ||
#Si la barra es homogénea, tiene masa <math>M</math> y longitud <math>L=2h</math> calcula el momento de inercia de la barra respecto a un eje paralelo al eje <math>O_1Z_1</math> que pase por <math>O_1</math>. | #Si la barra es homogénea, tiene masa <math>M</math> y longitud <math>L=2h</math> calcula el momento de inercia de la barra respecto a un eje paralelo al eje <math>O_1Z_1</math> que pase por <math>O_1</math>. | ||
| + | |||
| + | ==[[ Cono rotando con punto fijo (Nov. 2018) | Cono rotando con punto fijo ]]== | ||
| + | [[File:MRGIC_cono_rotando_enunciado.png|right]] | ||
| + | Un cono con ángulo de abertura <math>\pi/4</math> y radio de la base <math>R</math> se mueve de modo | ||
| + | que rueda sin deslizar sobre el plano fijo "1" y su vértice <math>C</math> permanece fijo | ||
| + | sobre el eje <math>OZ_1</math>. La base del cono permanece siempre perpendicular al plano <math>OX_1Y_1</math>. El sólido auxiliar "0" se escoge de modo que el plano | ||
| + | <math>X_0Z_0</math> contiene siempre a los puntos <math>A</math>, <math>B</math> y <math>C</math> del cono. El sólido "0" | ||
| + | rota alrededor del eje <math>OZ_1</math> con velocidad angular constante <math>\vec{\Omega} = | ||
| + | \Omega\,\vec{k}_{0,1}</math>. | ||
| + | #Localiza y dibuja los ejes de rotación de los movimientos {01}, {20} y {21}. ¿Qué tipo de eje es cada uno de ellos? | ||
| + | #Calcula las reducciones cinemáticas en <math>G</math> de los tres movimientos relativos. | ||
| + | #Calcula las derivadas temporales en <math>G</math> de los tres movimientos relativos. | ||
última version al 16:42 29 nov 2018
1 Barra deslizando sobre esquina
Una barra (sólido "2") se apoya en una esquina (sólido "1") como se indica
en la figura. El punto A de la barra se mueve sobre una barra fija (también
sólido "1") con velocidad constante  . En el instante indicado en la
figura la barra forma un ángulo π / 4 con el eje O1X1. Las preguntas que
se plantean a continuación se refieren todas al instante indicado en la figura.
. En el instante indicado en la
figura la barra forma un ángulo π / 4 con el eje O1X1. Las preguntas que
se plantean a continuación se refieren todas al instante indicado en la figura.
- Expresa el vector geométrico
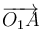 .
.
- Encuentra gráficamente la posición del C.I.R. del movimiento {21}.
- vector de posición del C.I.R. respecto del origen O1.
- Encuentra la reducción cinemática del movimiento {21} en el punto A. ¿Cuál es la velocidad
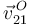 ?
?
- Si la barra es homogénea, tiene masa M y longitud L = 2h calcula el momento de inercia de la barra respecto a un eje paralelo al eje O1Z1 que pase por O1.
2 Cono rotando con punto fijo
Un cono con ángulo de abertura π / 4 y radio de la base R se mueve de modo
que rueda sin deslizar sobre el plano fijo "1" y su vértice C permanece fijo
sobre el eje OZ1. La base del cono permanece siempre perpendicular al plano OX1Y1. El sólido auxiliar "0" se escoge de modo que el plano
X0Z0 contiene siempre a los puntos A, B y C del cono. El sólido "0"
rota alrededor del eje OZ1 con velocidad angular constante 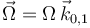 .
.
- Localiza y dibuja los ejes de rotación de los movimientos {01}, {20} y {21}. ¿Qué tipo de eje es cada uno de ellos?
- Calcula las reducciones cinemáticas en G de los tres movimientos relativos.
- Calcula las derivadas temporales en G de los tres movimientos relativos.







