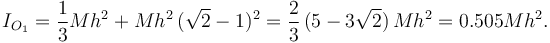De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una barra (sólido "2") se apoya en una esquina (sólido "1") como se indica en la figura. El punto $A$ de la barra se mueve sobre una barra fija (también sólido "1") con velocidad constante $\vec{v}_0$ . En el instante indicado en la figura la barra forma un ángulo $π / 4$ con el eje $O 1 X 1$ . Las preguntas que se plantean a continuación se refieren todas al instante indicado en la figura.

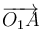Expresa el vector geométrico $\overrightarrow{O_1A}$ .
Encuentra gráficamente la posición del C.I.R. del movimiento {21}.
vector de posición del C.I.R. respecto del origen $O 1$ .
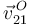Encuentra la reducción cinemática del movimiento {21} en el punto $A$ . ¿Cuál es la velocidad $\vec{v}^{\,O}_{21}$ ?
Si la barra es homogénea, tiene masa $M$ y longitud $L = 2 h$ calcula el momento de inercia de la barra respecto a un eje paralelo al eje $O 1 Z 1$ que pase por $O 1$ .

2 Solución

2.1 Vector geométrico 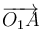$\overrightarrow{O_1A}$

Como el ángulo que forma la barra con el eje $O X 1$ es $π / 4$ , la componentes del vector $\overrightarrow{OA}$ son iguales sobre los ejes $O X 1$ y $O Y 1$ ,

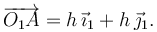
$\overrightarrow{O_1A} = h\,\vec{\imath}_1 + h\,\vec{\jmath}_1.$

2.2 Posición del C.I.R.

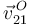Como se indica en la figura de la derecha, la velocidad $\vec{v}^{\,A}_{21}$ es paralela al eje $O 1 X 1$ , mientras que la velocidad $\vec{v}^{\,O}_{21}$ es paralela a la propia barra, pues esta desliza sobre la esquina. Trazando las rectas perpendiculares a las velocidades respectivas en los dos puntos encontramos el C.I.R. $I 21$ en el punto en que se cortan. El vector de posición es

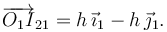
$\overrightarrow{O_1I}_{21} = h\,\vec{\imath}_1 - h\,\vec{\jmath}_1.$

2.3 Reducción cinemática en $A$

Hay tres maneras de hacer este apartado: a través del C.I.R., usando que la velocidad 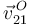$\vec{v}^{\,O}_{21}$ es paralela a la propia barra o usando la condición de equiproyectividad.

2.3.1 Usando el C.I.R.

Al ser un movimiento plano sabemos que el vector rotación es de la forma

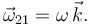
$\vec{\omega}_{21} = \omega\,\vec{k}.$

Como la velocidad en el C.I.R. es cero tenemos

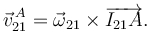
$\vec{v}^{\,A}_{21} = \vec{\omega}_{21}\times\overrightarrow{I_{21}A}.$

El vector geométrico es

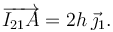
$\overrightarrow{I_{21}A} = 2h\,\vec{\jmath}_1.$

Por tanto tenemos

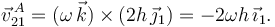
$\vec{v}^{\,A}_{21} = (\omega\,\vec{k})\times(2h\,\vec{\jmath}_1) = -2\omega h\,\vec{\imath}_1.$

Como por otro lado tenemos 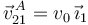$\vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1$ tenemos

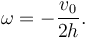
$\omega = -\dfrac{v_0}{2h}.$

La reducción cinemática en $A$ es

$\vec{\omega} = -\dfrac{v_0}{2h}\,\vec{k}, \qquad\qquad \vec{v}^{\,A}_{21}= v_0\,\vec{\imath}_1.$

Ahora podemos calcular la velocidad en $O$

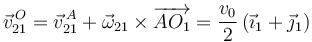
$\vec{v}^{\,O}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AO_1} = \dfrac{v_0}{2}\,(\vec{\imath}_1 + \vec{\jmath}_1)$

2.3.2 Usando la dirección conocida de la velocidad en $O$

De nuevo razonamos que, al ser un movimiento plano, el vector rotación es de la forma

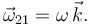
$\vec{\omega}_{21} = \omega\,\vec{k}.$

Sabemos que la velocidad en $O$ debe ser paralela al vector 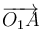$\overrightarrow{O_1A}$ . Usando el Teorema de Chasles tenemos

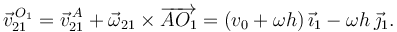
$\vec{v}^{\,O_1}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AO_1} = (v_0+\omega h)\,\vec{\imath}_1 - \omega h\,\vec{\jmath}_1.$

Imponiendo que debe ser paralelo a la barra tenemos

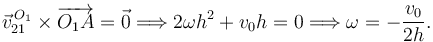
$\vec{v}^{\,O_1}_{21}\times\overrightarrow{O_1A} = \vec{0} \Longrightarrow 2\omega h^2 + v_0h=0 \Longrightarrow \omega = -\dfrac{v_0}{2h}.$

Con lo que reobtenemos el resultado anterior.

2.3.3 Usando equiproyectividad

De nuevo partimos de que, al ser un movimiento plano, el vector rotación es

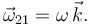
$\vec{\omega}_{21} = \omega\,\vec{k}.$

La velocidad en $O$ debe ser paralela a la barra, por lo que debe tener la forma

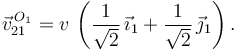
$\vec{v}^{\,O_1}_{21} = v\,\left(\dfrac{1}{\sqrt{2}}\,\vec{\imath}_1 + \dfrac{1}{\sqrt{2}}\,\vec{\jmath}_1\right).$

La condición de equiproyectividad impone que

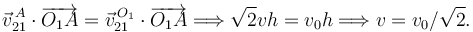
$\vec{v}^{\,A}_{21}\cdot\overrightarrow{O_1A} =\vec{v}^{\,O_1}_{21}\cdot\overrightarrow{O_1A} \Longrightarrow \sqrt{2}vh = v_0h \Longrightarrow v = v_0/\sqrt{2}.$

La velocidad en $O 1$ es

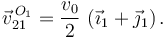
$\vec{v}^{\,O_1}_{21} = \dfrac{v_0}{2}\,\left(\vec{\imath}_1 + \vec{\jmath}_1\right).$

Y ahora podemos usar el Teorema de Chasles entre los puntos $O 1$ y $A$ para obtener $\vec{\omega}_{21}$ .

2.4 Momento de inercia en $O 1$

Lo mas sencillo es utilizar el Teorema de los ejes paralelos. El momento de inercia respecto a un eje perpendicular a la barra que pase por su centro de masas es

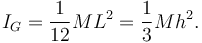
$I_G = \dfrac{1}{12}ML^2 = \dfrac{1}{3}Mh^2.$

El momento de inercia pedido se puede calcular así

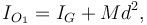
$I_{O_1} = I_G + Md^2,$

donde $d$ es la distancia entre el centro de la barra, $G$ y el punto $O 1$ . Del dibujo podemos deducir

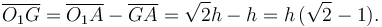
$\overline{O_1G} = \overline{O_1A} - \overline{GA} = \sqrt{2}h - h = h\,(\sqrt{2}-1).$

Entonces

$I_{O_1} = \dfrac{1}{3}Mh^2 + Mh^2\,(\sqrt{2}-1)^2 = \dfrac{2}{3}\,(5-3\sqrt{2})\,Mh^2 = 0.505Mh^2.$

Barra deslizando sobre esquina (Nov. 2018)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector geométrico $\overrightarrow{O_1A}$

2.2 Posición del C.I.R.

2.3 Reducción cinemática en $A$

2.3.1 Usando el C.I.R.

2.3.2 Usando la dirección conocida de la velocidad en $O$

2.3.3 Usando equiproyectividad

2.4 Momento de inercia en $O 1$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra deslizando sobre esquina (Nov. 2018)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector geométrico

2.2 Posición del C.I.R.

2.3 Reducción cinemática en A

2.3.1 Usando el C.I.R.

2.3.2 Usando la dirección conocida de la velocidad en O

2.3.3 Usando equiproyectividad

2.4 Momento de inercia en O1

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1 Vector geométrico $\overrightarrow{O_1A}$

2.3 Reducción cinemática en $A$

2.3.2 Usando la dirección conocida de la velocidad en $O$

2.4 Momento de inercia en $O 1$