|
|
| (9 ediciones intermedias no se muestran.) |
| Línea 76: |
Línea 76: |
| | | | |
| | <center>[[Archivo:srsr.png|300px]]</center> | | <center>[[Archivo:srsr.png|300px]]</center> |
| | + | |
| | + | ==Grados de libertad de un sólido== |
| | + | El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema. |
| | + | |
| | + | ¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos. |
| | + | |
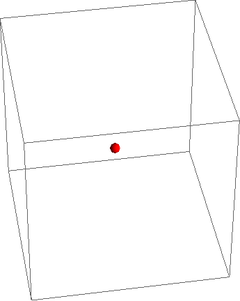
| | + | Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas. |
| | + | |
| | + | {| class="bordeado" |
| | + | |- |
| | + | | [[Archivo:solido-1-particula.png|240px]] |
| | + | | [[Archivo:solido-2-particulas.png|240px]] |
| | + | | [[Archivo:solido-3-particulas.png|240px]] |
| | + | |} |
| | + | |
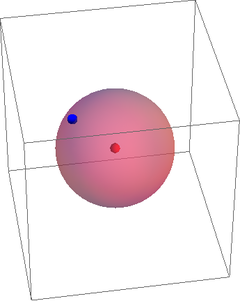
| | + | Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio <math>d_{12}</math> alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo). |
| | + | |
| | + | Una tercera partícula se encuentra a una distancia <math>d_{13}</math> de la primera y a una distancia <math>d_{23}</math> de la segunda. La posición de esta tercera partícula se encuentra por tanto sobre la circunferencia intersección de una esfera de radio <math>d_{13}</math> alrededor de la primera y una esfera de radio <math>d_{23}</math> alrededor de la segunda, y para localizar una posición concreta sobre una circunferencia solo necesitamos 1 variable. |
| | + | |
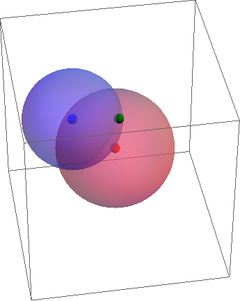
| | + | Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales. |
| | + | |
| | + | Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido. |
| | + | |
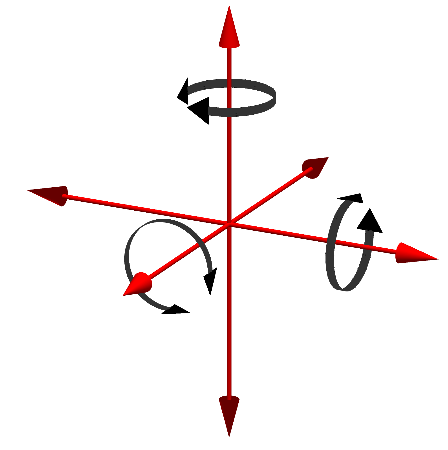
| | + | En términos geométricos, mientras que una partícula solo posee los grados de libertad correspondientes a 3 traslaciones independientes (en la dirección de OX, de OY y de oZ, por ejemplo), un sólido incorpora además 3 posibles rotaciones respecto a ejes diferentes, resultando un total de 3 + 3 = 6 grados de libertad. |
| | + | |
| | + | <center>[[Archivo:grados-libertad-solido.png]]</center> |
| | + | Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6. |
| | | | |
| | ==Movimientos rígidos== | | ==Movimientos rígidos== |
| Línea 95: |
Línea 122: |
| | Supongamos que sometemos a todo el sólido a una traslación <math>\Delta\vec{r}</math>. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que <math>A</math> es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A. | | Supongamos que sometemos a todo el sólido a una traslación <math>\Delta\vec{r}</math>. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que <math>A</math> es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A. |
| | <center>[[Archivo:tras-rot.png|577px]]</center> | | <center>[[Archivo:tras-rot.png|577px]]</center> |
| - | El punto A no tiene nada de especial. Podemos aplicar el mismo razonamiento a cualquier otro punto de referencia y el resultado es el mismo, es más, aunque el desplazamiento variará en cada caso, la rotación que debemos efectuar es independiente del punto de referencia que hayamos tomado.
| |
| - |
| |
| - | <center>[[Archivo:tras-rot-02.png|523px]]</center>
| |
| - | Para ello consideramos el movimiento respecto a un punto dado A del sólido. Este punto experimenta un cierto desplazamiento. El resto de los puntos experimenta el mismo desplazamiento que A más un movimiento rígido alrededor de A, que constituye una rotación.
| |
| | | | |
| | ==Traslaciones== | | ==Traslaciones== |
| Línea 106: |
Línea 129: |
| | ==Movimiento general de un sólido== | | ==Movimiento general de un sólido== |
| | {{ac|Movimiento general de un sólido rígido}} | | {{ac|Movimiento general de un sólido rígido}} |
| - | ===Expresión de las traslaciones===
| |
| - | En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento
| |
| - |
| |
| - | <center><math>\vec{r}=\vec{r}_0+\Delta \vec{r}\qquad\qquad \left\{ \begin{array}{rcl} x & = & x_0+ \Delta x \\ y & = & y_0+ \Delta y \\ z & = & z_0+ \Delta z \end{array}\right.</math></center>
| |
| - |
| |
| - | ===Expresión de las rotaciones===
| |
| - | Supongamos que en una rotación el punto fijo es O, que tomaremos como origen de coordenadas. En una rotación, cualquier punto pasará de la posición
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}_0=\vec{r}_0=X\vec{\imath}+Y\vec{\jmath}+Z\vec{k}</math></center>
| |
| - |
| |
| - | a la posición
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}=\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}</math></center>
| |
| - |
| |
| - | Deseamos establecer la relación entre estos dos vectores.
| |
| - |
| |
| - | Para ello, emplearemos dos sistemas de referencia. El sistema “1” es el que consideramos fijo y respecto al cual se mueve el sólido. Los dos vectores que acabamos de escribir estarían expresados en la base 1. El otro (“2”) es uno móvil que gira con el sólido en todo momento.
| |
| - |
| |
| - | En ese caso, al estar ligado al sólido, la posición de los puntos de éste son constantes en todo momento. Es decir, la posición de P
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}=\vec{r}=x\vec{\imath}_1+y\vec{\jmath}_1+z\vec{k}_1</math></center>
| |
| - |
| |
| - | se expresará en la base 2
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}=\vec{r}=X\vec{\imath}_2+Y\vec{\jmath}_2+Z\vec{k}_2</math></center>
| |
| - |
| |
| - | Nótese que en ambos casos se trata del mismo vector, expresado en dos bases distintas.
| |
| - |
| |
| - | <center>[[Archivo:rotacion-oz.png]]</center>
| |
| - | Para hallar las componentes en la base 1 proyectamos sobre cada vector de esta base
| |
| - |
| |
| - | <center><math>x = \vec{\imath}_1\cdot\vec{r} = (\vec{\imath}_1\cdot\vec{\imath}_2)X+(\vec{\imath}_1\cdot\vec{\jmath}_2)Y + (\vec{\imath}_1\cdot\vec{k}_2)Z</math></center>
| |
| - |
| |
| - | y análogamente para las otras dos componentes. Podemos escribir este resultado en forma matricial
| |
| - |
| |
| - | <center><math>\begin{pmatrix}x \\ y \\ z\end{pmatrix}=\begin{pmatrix} \vec{\imath}_1\cdot\vec{\imath}_2 & \vec{\imath}_1\cdot\vec{\jmath}_2 & \vec{\imath}_1\cdot\vec{k}_2 \\
| |
| - | \vec{\jmath}_1\cdot\vec{\imath}_2 & \vec{\jmath}_1\cdot\vec{\jmath}_2 & \vec{\jmath}_1\cdot\vec{k}_2 \\
| |
| - | \vec{k}_1\cdot\vec{\imath}_2 & \vec{k}_1\cdot\vec{\jmath}_2 & \vec{k}_1\cdot\vec{k}_2 \end{pmatrix}\cdot \begin{pmatrix}X \\ Y \\ Z\end{pmatrix}</math></center>
| |
| - |
| |
| - | que podemos abreviar como
| |
| - |
| |
| - | <center><math>\vec{r}=\overline{\overline{R}}\cdot\vec{r}_0</math></center>
| |
| - |
| |
| - | donde <math>\overline{\overline{R}}</math> es la ''matriz de rotación'' que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.
| |
| - |
| |
| - | Vemos que los elementos de la matriz de rotación son los productos escalares entre los vectores de la base fija en el sólido y la fija en el laboratorio. Por ser unitarios todos los vectores estos elementos son los cosenos directores
| |
| - |
| |
| - | <center><math>\vec{\imath}_1\cdot\vec{\imath}_2 = \cos(\vec{\imath}_1,\vec{\imath}_2)</math></center>
| |
| - |
| |
| - | Asmismo, cada fila corresponde a las componentes de un vector de la base fija (1) expresado en la base ligada al sólido (2), y cada columna un vector de la base ligada al sólido expresado en la base fija. Simbólicamente
| |
| - |
| |
| - | <center><math>\overline{\overline{R}}=\begin{pmatrix}\leftarrow & \vec{\imath}_1 & \rightarrow \\ \leftarrow & \vec{\jmath}_1 & \rightarrow \\ \leftarrow & \vec{k}_1 & \rightarrow \end{pmatrix} = \begin{pmatrix} \uparrow & \uparrow & \uparrow \\ \vec{\imath}_2 & \vec{\jmath}_2 & \vec{k}_2 \\ \downarrow & \downarrow & \downarrow\end{pmatrix}</math></center>
| |
| - |
| |
| - | ====Propiedades de la matriz de rotación====
| |
| - | ;Tiene tres grados de libertad: De acuerdo con la expresión anterior, parece que para expresar una rotación hay que proporcionar 9 parámetros, esto es, que tiene 9 grados de libertad. No es así, ya que tenemos seis vínculos entre las componentes. Por ser ortonormal cada base
| |
| - |
| |
| - | <center><math>\begin{array}{ccccccc}
| |
| - | \vec{\imath}_1\cdot\vec{\imath}_1 & = & \vec{\jmath}_1\cdot\vec{\jmath}_1 & = &
| |
| - | \vec{k}_1\cdot\vec{k}_1& = & 1\\ &&&&&& \\
| |
| - | \vec{\imath}_1\cdot\vec{\jmath}_1 & = & \vec{\jmath}_1\cdot\vec{k}_1 & = &
| |
| - | \vec{k}_1\cdot\vec{\imath}_1& = & 0\end{array}</math></center>
| |
| - |
| |
| - | :Estos seis vínculos reducen el número de grados de libertad a 3, que pueden ser tres ángulos de orientación, como los ángulos de Euler.
| |
| - |
| |
| - | ;Es ortogonal: Una matriz es ortogonal cuando su traspuesta coincide con su inversa. Si una rotación dada lleva de la base 1 a la base 2, la rotación inversa será la que devuelve la base 2 a la base 1. Por la construcción de la matriz, el intercambiar 1 por 2 equivale a intercambiar filas por columnas, esto es, hallar la traspuesta. Por tanto
| |
| - |
| |
| - | <center><math>\overline{\overline{R}}^{-1}=\overline{\overline{R}}^T\,\qquad\Rightarrow\qquad \overline{\overline{R}}^T\overline{\overline{R}}=\overline{\overline{R}}\overline{\overline{R}}^T=\overline{\overline{1}}</math></center>
| |
| - |
| |
| - | :(empleamos <math>\overline{\overline{1}}</math> en vez de <math>\overline{\overline{I}}</math>, para reservar esta letra para los momentos de inercia) Esta propiedad equivale a lo que hemos mencionado de que las dos bases 1 y 2 son bases ortonormales.
| |
| - |
| |
| - | ;Es unitaria: Una matriz es unitaria si su determinante vale la unidad. Es consecuencia inmediata de lo anterior
| |
| - |
| |
| - | <center><math>1=\left|\overline{\overline{1}}\right|=\left|\overline{\overline{R}}\overline{\overline{R}}^T\right|=\left|\overline{\overline{R}}\right|\left|\overline{\overline{R}}^T\right|=\left|\overline{\overline{R}}\right|^2\qquad\Rightarrow\qquad \left|\overline{\overline{R}}\right|=\pm 1</math></center>
| |
| - |
| |
| - | :La raíz negativa la descartamos, ya que corresponde a las simetrías, que hemos considerado como imposibles en el movimiento de un sólido real.
| |
| - |
| |
| - | ====Teorema de Euler. Eje de rotación====
| |
| - | Hemos definido como un movimiento rígido que deja un punto fijo. Euler demostró que esto implica que no hay un solo punto fijo, sino toda una recta que pasa por O. Esta recta es el llamado ''eje de rotación''.
| |
| - |
| |
| - | La demostración se basa en que debe haber un vector no afectado por la rotación, esto es,
| |
| - |
| |
| - | <center><math>\overline{\overline{R}}\vec{u}=\vec{u}</math></center>
| |
| - |
| |
| - | Si este vector <math>\vec{u}</math> existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.
| |
| - |
| |
| - | En términos algebraicos esto equivale a decir que existe un autovalor unidad, siendo <math>\vec{u}</math> el autovector correspondiente. La condición para que ello ocurra es que
| |
| - |
| |
| - | <center><math>\overline{\overline{R}}\vec{u}=\vec{u}\qquad\Rightarrow\qquad \left(\overline{\overline{R}}-\overline{\overline{1}}\right)\vec{u}=\vec{0}´\qquad\Rightarrow\qquad \left|\overline{\overline{R}}-\overline{\overline{1}}\right|=0</math></center>
| |
| - |
| |
| - | Veamos que es cierto:
| |
| - |
| |
| - | <center><math>\left|\overline{\overline{R}}-\overline{\overline{1}}\right|=\left|(\overline{\overline{R}}-\overline{\overline{1}})^T\right|=\left|\overline{\overline{R}}^T-\overline{\overline{1}}\right|=\left|\overline{\overline{R}}^T\left(\overline{\overline{1}}-\overline{\overline{R}}\right)\right|=\left|\overline{\overline{R}}^T\right|\left|\overline{\overline{1}}-\overline{\overline{R}}\right|=-\left|\overline{\overline{R}}-\overline{\overline{1}}\right|</math></center>
| |
| - |
| |
| - | y por tanto
| |
| - |
| |
| - | <center><math>\left|\overline{\overline{R}}-\overline{\overline{1}}\right|=-\left|\overline{\overline{R}}-\overline{\overline{1}}\right|\qquad\Rightarrow\qquad \left|\overline{\overline{R}}-\overline{\overline{1}}\right|=0</math></center>
| |
| - |
| |
| - | Por tanto existe el autovalor unidad, y el autovector correspondiente nos da el eje de rotación.
| |
| - |
| |
| - | Esto nos da otra forma de parametricar las rotaciones: con dos ángulos (por ejemplo los de las coordenadas esféricas) damos la orientación de este vector director y con un tercer ángulo medimos cuánto ha girado el sólido en torno al eje.
| |
| - |
| |
| - | Como consecuencia del teorema de Euler, cualquier vector perpendicular al eje de giro sigue siendo perpendicular tras la rotación. Si el vector <math>\vec{v}_2</math> se transforma en el <math>\vec{v}</math>
| |
| - |
| |
| - | <center><math>\vec{u}\cdot\vec{v}_2=0\qquad\Rightarrow\qquad \vec{u}\cdot\vec{v}=\vec{u}\overline{\overline{R}}\vec{v}_2 = (\vec{u}\overline{\overline{R}})\vec{v}_2=\vec{u}\cdot\vec{v}_2=0</math></center>
| |
| - |
| |
| - | Cualquier otro vector podrá descomponerse en una parte paralela al eje de giro (que no se verá afectada por la rotación) más una parte ortogonal al eje (que gira un cierto ángulo en torno al eje, manteniéndose ortogonal).
| |
| - |
| |
| - | ===Movimiento general. Teorema de Chasles===
| |
| - | El caso general, según hemos visto, es una composición de una rotación y un desplazamiento en una dirección arbitraria.
| |
| - |
| |
| - | Chasles generalizó el teorema de Euler, observando que ese desplzamiento arbitrario puede descomponerse en una traslación paralela al eje de rotación y en una ortogonal a él. la parte ortogonal puede englobarse en la rotación, quedando solo la paralela.
| |
| - |
| |
| - | Por tanto, el movimiento general de un sólido se reduce a una rotación en torno a un eje y un desplazamiento en la dirección de este eje (que en este contexto se denomina ''eje de rotación y mínimo deslizamiento''). Este movimiento se denomina “un tornillo” por su analogía con la conducta de esta herramienta.
| |
| - |
| |
| - | ==Campo de velocidades==
| |
| - | Cuando un sólido rígido se mueve efectúa en cada instante un movimiento rígido infinitesimal.
| |
| - |
| |
| - | Como en los movimientos finitos, consideraremos dos sistemas de referencia: el 1, que consideramos como fijo y el 2, ligado al sólido.
| |
| - |
| |
| - | Dado que un punto P del espacio puede considerarse simultáneamente como parte del sistema de referencia 1 y como parte del sistema 2, emplearemos la siguiente notación para indicar la velocidad del punto P
| |
| - |
| |
| - | <center>[[Archivo:vP21.png]]</center>
| |
| - |
| |
| - | Esta notación puede parece un poco excesiva en este contexto, pero será de gran utilidad al considerar el [[Cinemática_del_movimiento_relativo_(CMR)|movimiento relativo]].
| |
| - |
| |
| - | De acuerdo con el teorema de Chasles, este movimiento instantáneo se compondrá de una rotación diferencial alrededor de un eje (que ahora será eje ''instantáneo'' de rotación y mínimo deslizamiento, ya que puede cambiar de un instante a otro) y de un desplazamiento.
| |
| - |
| |
| - | Si tomamos como referencia el punto O (“centro de reducción”) la velocidad de cualquier punto será la suma vectorial de la traslación de O más la rotación alrededor de un eje que pasa por O.
| |
| - |
| |
| - | Para la velocidad de la rotación no tenemos más que considerar de nuevo qué le ocurre a la base ligada al sólido.
| |
| - |
| |
| - | Si consideramos un punto P del sólido, su expresión en la bae ligada al sólido será
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}=x_2\vec{\imath}_2+y_2\vec{\jmath}_2+z_2\vec{k}_2</math></center>
| |
| - |
| |
| - | Este vector será constante en el sistema de referencia ligado al sólido, pero no en el sistema fijo 1. Si derivamos esta expresión en el sistema de referencia 1, solo son dependientes del tiempo los vectores de la base
| |
| - |
| |
| - | <center><math>\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OP}\right|_1=x_2\left.\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}\right|_1+y_2\left.\frac{\mathrm{d}\vec{\jmath}_2}{\mathrm{d}t}\right|_1+z_2\left.\frac{\mathrm{d}\vec{k}_2}{\mathrm{d}t}\right|_1</math></center>
| |
| - |
| |
| - | ¿Cuánto vale la derivada respecto al tiempo de <math>\vec{\imath}_2</math>? El extremo de este vector está realizando un movimiento circular instantáneo alrededor del eje de rotación y por tanto su velocidad cumple la relación
| |
| - |
| |
| - | <center><math>\left.\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}\right|_1=\vec{\omega}_{21}\times \vec{\imath}_2</math></center>
| |
| - |
| |
| - | y lo mismo para los otros dos vectores de la base, que giran con la misma velocidad angular (si las velocidades angulares fueran diferentes el sólido dejaría de ser rígido, ya que los vectores de la base se acercarían o alejarían). Por tanto,
| |
| - |
| |
| - | <center><math>\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OP}\right|_1=x_2(\vec{\omega}_{21}\times \vec{\imath}_2)+y_2(\vec{\omega}_{21}\times \vec{\jmath}_2)+z_2(\vec{\omega}_{21}\times \vec{k}_2)=\vec{\omega}_{21}\times(x_2\vec{\imath}_2+y_2\vec{\jmath}_2+z_2\vec{k}_2)=\vec{\omega}_{21}\times\overrightarrow{OP}</math></center>
| |
| - |
| |
| - | <center>[[Archivo:rotación-instantanea-base.png]]</center>
| |
| - | Por tanto, la velocidad debida a la rotación del sólido será, para todos los puntos,
| |
| - |
| |
| - | <center><math>\vec{v}_{21}^{Pr}=\vec{\omega}_{21}\times\overrightarrow{OP}</math></center>
| |
| - |
| |
| - | Aquí al vector <math>\vec{\omega}_{21}</math> se lo denomina ''vector rotación'' del sólido o velocidad angular instantánea del sólido. El criterio para asignar los subíndices es el mismo que para la velocidad lineal
| |
| - |
| |
| - | <center>[[Archivo:w21.png]]</center>
| |
| - |
| |
| - | A esta velocidad habrá que sumarle la de la traslación del punto O, que será común para todos los puntos
| |
| - |
| |
| - | <center><math>\vec{v}_{21}^{Pt}=\vec{v}^O_{21}</math></center>
| |
| - |
| |
| - | y por tanto la velocidad de cualquier punto del sólido es de la forma
| |
| - |
| |
| - | <center><math>\vec{v}^P_{21}=\vec{v}^O_{21}+\vec{\omega}_{21}\times \overrightarrow{OP}</math></center>
| |
| - |
| |
| - | ===Cambio del centro de reducción===
| |
| - | En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos
| |
| - |
| |
| - | <center><math>\vec{v}^P_{21}=\vec{v}^O_{21}+\vec{\omega}_{21}\times\left(\overrightarrow{OA}+\overrightarrow{AP}\right)=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AP}</math></center>
| |
| - |
| |
| - | es, decir, para cualquier par de puntos se cumple
| |
| - |
| |
| - | <center><math>\vec{v}^P_{21}=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AP}</math></center>
| |
| - |
| |
| - | o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par <math>\{\vec{\omega}_{21},\vec{v}^A_{21}\}</math> se lo denomina ''reducción cinemática'' del campo de velocidades en el punto A.
| |
| - |
| |
| - | ===Estructura del campo de velocidades===
| |
| - | ====Invariantes====
| |
| - | Hay dos cantidades que son iguales para todos los puntos del sólido:
| |
| - |
| |
| - | ;Velocidad angular: Es el ''invariante vectoral'' <math>\vec{\omega}_{21}</math> que, como hemos visto aparece en cualquier reducción cinemática. Es decir que cualquiera que sea el punto de referencia que tomemos, vemos al sólido girar instantáneamente con la misma velocidad angular.
| |
| - |
| |
| - | ;Velocidad de deslizamiento: Es el ''invariante escalar''. Si calculamos la componente de la velocidad de cada punto en la dirección de la velocidad angular tenemos
| |
| - |
| |
| - | <center><math>v_{Pd}=\vec{v}^P_{21}\cdot\vec{u}_\omega=\vec{v}^P_{21}\cdot\frac{\vec{\omega}_{21}}{|\vec{\omega}_{21}|} = \vec{v}^O_{21}\cdot\frac{\vec{\omega}_{21}}{|\vec{\omega}_{21}|}=v_{Od}</math></center>
| |
| - |
| |
| - | Atendiendo a estas dos cantidades, o para evitar divisiones por cero, a <math>\vec{\omega}_{21}</math> y <math>\vec{v}_{21}^2\cdot\vec{\omega}_{21}=v_d\vec{\omega}_{21}</math> tenemos los siguientes posibles estados de movimiento: reposo, traslación, rotación y movimiento helicoidal.
| |
| - | ====Reposo y traslación====
| |
| - | Si la velocidad angular es nula en un instante dado, la velocidad de todos los puntos del sólido es idéntica en dicho instante.
| |
| - |
| |
| - | <center><math>\vec{v}^P_{21}=\vec{v}^O_{21}+\overbrace{\vec{\omega}_{21}}^{=\vec{0}}\times\overrightarrow{OP}=\vec{v}^O_{21}</math></center>
| |
| - |
| |
| - | En particular, si un punto tiene velocidad nula, todos tienen velocidad nula. Se dice entonces que el sólido está en un estado de reposo, que puede ser instantáneo o permanente.
| |
| - |
| |
| - | Si la velocidad de un punto (y, por tanto, de todos) no es nula, se dice que estamos en una traslación. Las traslaciones pueden ser instantáneas o permanentes.
| |
| - |
| |
| - | [[Archivo:noria-traslacion.gif|right]]
| |
| - |
| |
| - | Si fijamos un sistema de ejes al sólido, estos mantienen su orientación en un movimiento de traslación.
| |
| - |
| |
| - | Equivalentemente, el movimiento de traslación se puede enunciar afirmando que si tres puntos no colineales del sólido tienen la misma velocidad, todos los demás también tienen la misma.
| |
| - |
| |
| - | Hay que insistir en que hablamos de velocidades instantáneas y del movimiento relativo de los diferentes puntos del sólido. Un movimiento de traslación NO significa que el sólido se mueve en línea recta, o a velocidad constante.
| |
| - |
| |
| - | Por ejemplo, consideremos el movimiento de un vagón de una noria. Puesto que éste no se da la vuelta, sino que conserva en todo momento su orientación vertical, llegamos a la conclusión de que el sólido experimenta un movimiento de traslación. Cada uno de sus puntos se mueve en cada instante con la misma velocidad que el resto de los puntos, aunque esta velocidad sea cambiante.
| |
| - |
| |
| - | En el caso más restrictivo
| |
| - |
| |
| - | <center><math>\vec{\omega}_{21}=\vec{0} \quad \forall t</math></center>
| |
| - |
| |
| - | implica un movimiento de traslación permanente: los ejes ligados al sólido conservan su orientación en cada instante y el movimiento de cada uno de los puntos del sólido reproduce exactamente el de cualquier otro de ellos.
| |
| - |
| |
| - | En una traslación permanente, la posición relativa de un punto cualquiera B respecto a otro punto arbitrario A se mantiene constante en módulo, dirección y sentido.
| |
| - |
| |
| - | <center><math>\frac{\mathrm{d}\overrightarrow{AB}}{\mathrm{d}t}=\vec{v}_{21}^B-\vec{v}^A_{21}=\overbrace{\vec{\omega}_{21}}^{=\vec{0}}\times\overrightarrow{AB}= \vec{0}\qquad\Rightarrow\qquad \overrightarrow{AB}=\mathrm{cte}</math></center>
| |
| - |
| |
| - | Un movimiento de traslación permanente no tiene por qué ser ni rectilíneo ni uniforme. Como en el caso de la noria, es posible que cada uno de los puntos describa una circunferencia en torno a un centro (siendo este centro diferente para cada punto del sólido).
| |
| - |
| |
| - | ====Movimiento de rotación y helicoidal====
| |
| - | Si la velocidad angular es no nula, ya la velocidad no será la misma en todos los puntos. Atendiendo a la velocidad de deslizamiento, tenemos dos casos:
| |
| - |
| |
| - | ;Movimiento de rotación: Si la velocidad de deslizamiento es nula, <math>v_d=0</math> o, equivalentemente, si <math>\vec{v}^O_{21}\cdot\vec{\omega}_{21}= 0</math>
| |
| - |
| |
| - | ;Movimiento helicoidal: Si la velocidad de deslizamiento es distinta de cero, <math>v_d\neq 0</math>, o equivalentemente si <math>\vec{v}^O_{21}\cdot\vec{\omega}_{21}\neq 0</math>
| |
| - |
| |
| - | Estos dos movimientos comparten bastantes propiedades, y poseen algunas diferencias.
| |
| - |
| |
| - | * Si dos puntos están en una recta paralela a la velocidad angular, tienen la misma velocidad
| |
| - |
| |
| - | <center><math>\overrightarrow{PQ}\parallel \vec{\omega}_{21}\qquad\Rightarrow\qquad \vec{v}^P_{21}=\vec{v}_{21}^Q</math></center>
| |
| - |
| |
| - | :Esto permite reducir el estudio a lo que ocurre en planos perpendiculares a la velocidad angular, ya que la distribución de velocidades en estos planos paralelos será idéntica.
| |
| - |
| |
| - | *Inversamente, si dos puntos tienen la misma velocidad, la velocidad angular será paralela a la recta que pasa por estos dos puntos.
| |
| - |
| |
| - | * En cada uno de estos planos paralelos, existe un punto E cuya velocidad es la de deslizamiento (nula en el caso de rotación). Sea O el centro de reducción. Buscamos un punto I del plano normal a <math>\vec{\omega}_{21}</math> y que pasa por O, tal que <math>\vec{v}_{21}^I=v_d\vec{u}_\omega</math>
| |
| - |
| |
| - | <center><math>v_d\vec{u}_\omega = \vec{v}_{21}^I=\vec{v}^O_{21}+\vec{\omega}_{21}\times\overrightarrow{OI}</math></center>
| |
| - |
| |
| - | :multiplicando aquí vectorialmente por <math>\vec{\omega}_{21}</math> y aplicando las propiedades del doble producto vectorial
| |
| - |
| |
| - | <center><math>\vec{0}=\vec{\omega}_{21}\times\vec{v}^O_{21}+(\overbrace{\vec{\omega}_{21}\cdot\overrightarrow{OI}}^{=0})\vec{\omega}_{21}-|\vec{\omega}_{21}|^2\overrightarrow{OI}\qquad\Rightarrow\qquad \overrightarrow{OI}=\frac{\vec{\omega}_{21}\times\vec{v}^O_{21}}{|\vec{\omega}_{21}|^2}</math></center>
| |
| - |
| |
| - | * Existe una recta de puntos que tienen como velocidad la de deslizamiento (nula, en el caso de la rotación). Estos puntos constituyen el ''eje instantáneo de rotación y mínimo deslizamiento'' (EIRMD), que se reduce al ''eje instantáneo de rotación'' (EIR) si la velocidad de deslizamiento es nula. Es consecuencia de las dos propiedades anteriores. Si la velocidad del punto I es la de deslizamiento, la de cualquier otro punto situado en la recta que pasa por I y en la dirección de laa velocidad angular tendrá la misma velocidad. La ecuación del eje será
| |
| - |
| |
| - | <center><math>\overrightarrow{OE}= \frac{\vec{\omega}_{21}\times\vec{v}^O_{21}}{|\vec{\omega}_{21}|^2}+\lambda\vec{\omega}_{21}\qquad -\infty<\lambda<\infty</math></center>
| |
| - |
| |
| - | * La velocidad de cualquier punto que no pertenezca al EIRMD tendrá una componente paralela al eje y una ortogonal a él
| |
| - |
| |
| - | <center><math>\vec{v}^P_{21}=\overbrace{\vec{v}_{21}^I}^{\parallel \vec{\omega}_{21}}+\overbrace{\vec{\omega}_{21}\times\overrightarrow{IP}}^{\perp\vec{\omega}_{21}}</math></center>
| |
| - |
| |
| - | :La componente paralela es la velocidad de deslizamiento. La componente ortogonal representa la rotación en torno al EIRMD (EIR en su caso). Esta componente ortogonal está orientada según la regla de la mano derecha en torno al eje.
| |
| - |
| |
| - | <center>[[Archivo:Rotacion-pura-cenital.png]]</center>
| |
| - |
| |
| - | * La rapidez de cada punto depende de la distancia al eje como
| |
| - |
| |
| - | <center><math>|\vec{v}^P_{21}|=\sqrt{v_d^2+|\vec{\omega}_{21}|^2 R^2}</math></center>
| |
| - |
| |
| - | :siendo R la distancia del punto P al EIRMD. En el caso de una rotación (<math>v_d=0</math>) esta rapidez aumenta linealmente con la distancia al eje
| |
| - |
| |
| - | <center><math>|\vec{v}^P_{21}|=|\vec{\omega}_{21}| R</math></center>
| |
| - |
| |
| - | L estructura del campo de velocidades es entonces una combinación de avance a lo largo del EIRMD más una rotación en torno a éste.
| |
| - |
| |
| - | {| class="bordeado"
| |
| - | |-
| |
| - | ! Rotación
| |
| - | ! Helicoidal
| |
| - | |-
| |
| - | | [[Archivo:Rotacion-pura.png]]
| |
| - | | [[Archivo:Solido-helicoidal.png]]
| |
| - | |}
| |
| - |
| |
| - | Esto nos permite caracterizar completamente el movimiento
| |
| - |
| |
| - | * Si <math>\vec{\omega}_{21}=\vec{0}</math> y <math>\vec{v}^O_{21}=\vec{0}</math> el estado es de reposo (instantáneo, en general).
| |
| - | * Si <math>\vec{\omega}_{21}=\vec{0}</math> y <math>\vec{v}^O_{21}\neq \vec{0}</math> se trata de una traslación
| |
| - | * Si <math>\vec{\omega}_{21}\neq\vec{0}</math> y <math>\vec{v}^O_{21}\cdot\vec{\omega}_{21}=0</math> (porque <math>\vec{v}^O_{21}=\vec{0}</math> o es ortogonal a la velocidad angular) se trata de una rotación instantánea en torno a un EIR paralelo a la velocidad angular que pasa por <math>\overrightarrow{OI}</math> (para el cual se anula la velocidad en ese caso).
| |
| - | * Si <math>\vec{\omega}_{21}\neq\vec{0}</math> y <math>\vec{v}^O_{21}\cdot\vec{\omega}_{21}\neq 0</math> es un movimiento helicoidal instantáneo en torno a un EIRMD paralelo a la velocidad angular que pasa por <math>\overrightarrow{OI}</math> (para el cual la velocidad vale <math>v_d\vec{u}_\omega</math> y es paralela a la velocidad angular).
| |
| - |
| |
| - | <center>[[Archivo:flujo-cinematica.png]]</center>
| |
| - |
| |
| - | Al estudiar el movimiento de rotación y describir las velocidades según la ley se puede adquirir la idea errónea de que las partículas del sólido describen un movimiento circular. Eso '''NO''' es correcto. Lo que hemos hecho es describir la distribución ''instantánea'' de velocidades, esto es, qué velocidad tiene cada punto del sólido en un instante dado, pero no hemos analizado cómo se mueve cada punto a lo largo del tiempo (en términos llanos, hemos tomado una fotografía, no una película de vídeo).
| |
| - |
| |
| - | <center>[[Archivo:cicloide-rotacion.gif]]</center>
| |
| - |
| |
| - | Consideremos el caso de un cilindro que rueda sobre el suelo. La línea de contacto esta formada por puntos con velocidad nula y por tanto se trata de un eje instantáneo de rotación. El cilindro está efectuando una rotación pura instantánea en torno a esta línea de contacto (y no respecto al eje del cilindro, como podría pensarse), pero la trayectoria de cada punto del cilindro no es una circunferencia, sino una ''[[Movimiento cicloidal|cicloide]]'' (técnicamente, para los puntos que no son de la superficie exterior es una ''cicloide acortada'').
| |
| - |
| |
| - | La razón es que aunque instantáneamente esté rotando en torno a esta línea, el eje de rotación va cambiando en el tiempo.
| |
| | | | |
| | ==Campo de aceleraciones== | | ==Campo de aceleraciones== |
| - | Derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P
| + | {{ac|Campo de aceleraciones de un sólido}} |
| - | | + | |
| - | <center><math>\vec{a}_{21}^P = \left.\frac{\mathrm{d}\vec{v}_{21}^P}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{v}_{21}^O}{\mathrm{d}t}\right|_1 + \left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1\times\overrightarrow{OP}+\vec{\omega}_{21}\times\left.\frac{\mathrm{d}(\overrightarrow{OP})}{\mathrm{d}t}\right|_1</math></center>
| + | |
| - | | + | |
| - | Siendo
| + | |
| - | | + | |
| - | <center><math> \left.\frac{\mathrm{d}\vec{v}_{21}^O}{\mathrm{d}t}\right|_1=\vec{a}_{21}^O</math>{{qquad}}{{qquad}}<math>\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=\vec{\alpha}_{21}</math>{{qquad}}{{qquad}}<math>\left.\frac{\mathrm{d}(\overrightarrow{OP})}{\mathrm{d}t}\right|_1=\vec{v}_{21}^P-\vec{v}_{21}^O = \vec{\omega}_{21}\times\overrightarrow{OP}</math></center>
| + | |
| - | | + | |
| - | llegamos a la expresión del campo de aceleraciones
| + | |
| - | | + | |
| - | <center><math>\vec{a}_{21}^P = \vec{a}_{21}^O + \vec{\alpha}_{21}\times\overrightarrow{OP} + \vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{OP})</math></center>
| + | |
| - | | + | |
| - | A diferencia del campo de velocidades, el campo de aceleraciones no es equiproyectivo:
| + | |
| - | | + | |
| - | <center><math>(\vec{a}_{21}^P-\vec{a}_{21}^O)\cdot\overrightarrow{OP}=\overrightarrow{OP}\cdot(\vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{OP})) = -\left|\vec{\omega}_{21}\times\overrightarrow{OP}\right|^2</math></center>
| + | |
| - | | + | |
| - | Solo en el caso de traslación o reposo instantáneos se cumplirá la equiproyectividad.
| + | |
| - | | + | |
| - | Dos consideraciones prácticas.
| + | |
| - | | + | |
| - | * El campo de aceleraciones requiere conocer tres vectores (esto es, 9 datos, frente a los 6 del campo de velocidades):
| + | |
| - | ** La aceleración de un punto O, <math>\vec{a}_{21}^O</math>.
| + | |
| - | ** La velocidad angular instantánea, <math>\vec{\omega}_{21}</math>.
| + | |
| - | ** La aceleración angular, <math>\vec{\alpha}_{21}</math>, derivada temporal de la velocidad angular.
| + | |
| - | * La aceleración de un punto P se puede calcular derivando la velocidad sólo si se conoce ésta como función del tiempo <math>\vec{v}_{21}^P(t)</math>. Conocerla en un instante no es suficiente.
| + | |
| | | | |
| - | El conocimiento del campo de aceleraciones es especialmente útil cuando tenemos un punto fijo O, para el cual <math>\vec{a}_{21}^O=\vec{0}</math> y deseamos hallar la aceleración de otro punto en concreto, en particular, del centro de masas del sólido.
| + | ==Movimiento plano== |
| | + | {{ac|Movimiento plano de un sólido}} |
| | | | |
| | [[Categoría:Cinemática del sólido rígido (CMR)]] | | [[Categoría:Cinemática del sólido rígido (CMR)]] |
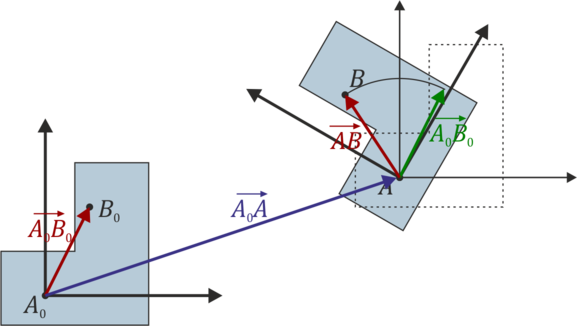
Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo con partículas B, C,… se cumple en todo instante
y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos
Cada ligadura geométrica implica una relación entre las velocidades posibles, ya que si la distancia entre un par de partículas es constante, no puede ser que sus velocidades nos digan que se están acercando o alejando. Obtenemos estas relaciones derivando en la expresión de los vínculos geométricos.
y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades.
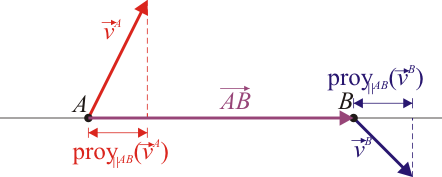
Esta condición nos dice que la velocidad relativa del punto B respecto del A (esto es, la que mide un observador situado en A y moviéndose con este punto) es ortogonal al vector de posición relativa
Esta condición cinemática se puede visualizar. Si estamos solidariamente unidos al punto A, vemos al punto B siempre a la misma distancia, es decir, se encuentra sobre la superficie de una esfera imaginaria. Al moverse sobre la esfera, su velocidad es tangente a la superficie y perpendicular al radio, que es el vector de posición relativo. Por tanto la velocidad relativa y la posición relativa son ortogonales.
Introduciendo el vector unitario en la dirección del segmento que une los dos puntos y en el sentido de la partícula A a la B.
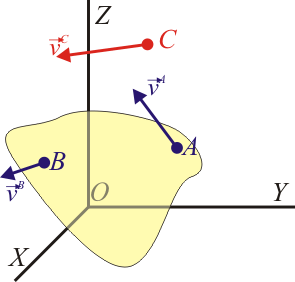
Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales.
Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a todo el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad.
Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido.
El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema.
¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos.
Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas.
Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio d12 alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo).
Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales.
Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido.
En términos geométricos, mientras que una partícula solo posee los grados de libertad correspondientes a 3 traslaciones independientes (en la dirección de OX, de OY y de oZ, por ejemplo), un sólido incorpora además 3 posibles rotaciones respecto a ejes diferentes, resultando un total de 3 + 3 = 6 grados de libertad.
Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6.
Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación.
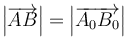
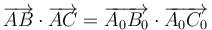
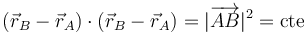
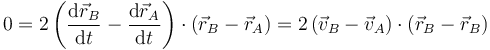
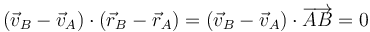
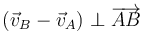
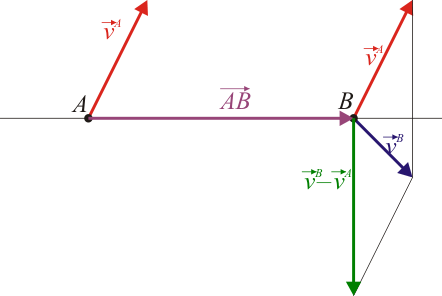
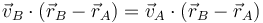
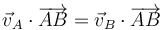
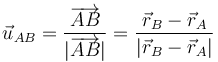
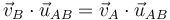


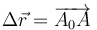
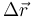 . para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A.
. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A.