Movimiento plano de un sólido
De Laplace
Contenido |
1 Definición de movimiento plano
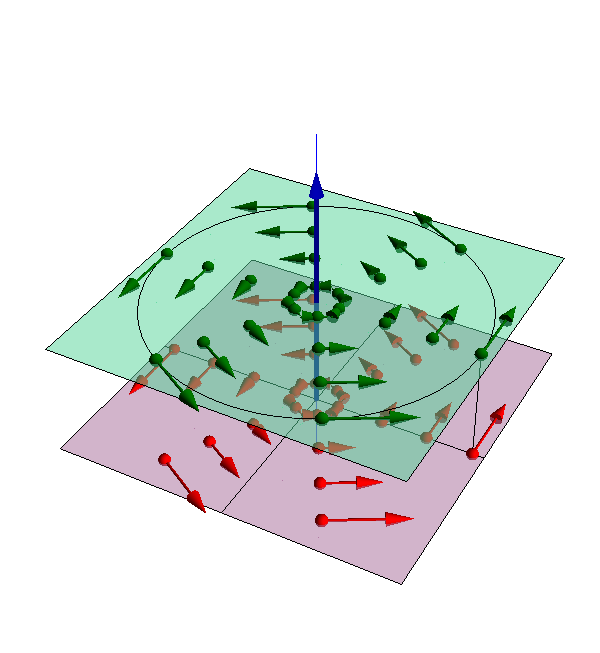
De entre los posibles movimientos de un sólido rígido, se dice que un sólido “2” realiza un movimiento plano respecto a un sólido “1” si los desplazamientos de todos sus puntos son permanentemente paralelos a un plano fijo en el sistema de referencia ligado al sólido 1. Este plano se denomina plano director, ΠD del movimiento plano.
Así, por ejemplo, el movimiento que realiza el chasis de un coche, respecto a la calzada por la que éste circula, es un movimiento plano.
También lo es el movimiento de una de sus ruedas cuando el coche avanza en línea recta. Sin embargo, en ese caso, el plano director no es el plano de la calzada, sino uno perpendicular a ella.
Cualquier plano paralelo a un plano director del movimiento {21} funciona también como plano director de dicho movimiento, por lo que ese término designa realmente a toda la familia de planos paralelos, caracterizados por una perpendicular común. Esta dirección normal a la familia de planos directores puede tomarse siempre como eje OZ (o cualquier otra dirección fija que nos convenga) y el vector unitario normal a los planos directores puede ser denotado como 
Matemáticamente tenemos que, para todo punto del sólido debe cumplirse en todo instante que
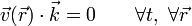
2 Propiedades del movimiento plano
Un movimiento plano de un sólido satisface, entre otras, las siguientes propiedades:
- 1) Las velocidades de todos los puntos del sólidos se encuentran contenidas en planos paralelos
- Es la condición definitoria del movimiento plano.
- 2) Las aceleraciones de todos los puntos son siempre paralelas al plano director
Puesto que la identidad anterior se cumple en cada instante, podemos derivar en ella respecto al tiempo
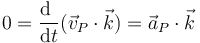
- 3) La trayectoria de cada uno de las partículas es plana
- Dada una partícula situada en un plano director, si la velocidad de la partícula es tangente a este plano, su posición inmediatamente después sigue estando en el mismo plano. Puesto que ello ocurre para todos los instantes, la posición de la partícula pertenece en todo momento al mismo plano y la trayectoria está contenida en él.
- 4) La velocidad angular del movimiento {21} es perpendicular al plano director (o nula)
- Por tratarse de un movimiento rígido, para cualesquiera dos puntos del sólido 2 se cumple
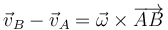
- siendo
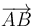 la posición relativa del punto “B” respecto al “A”.
la posición relativa del punto “B” respecto al “A”.
- Multiplicando aquí escalarmente por el vector normal al plano director
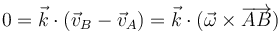

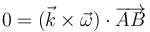
- Puesto que esta identidad debe cumplirse para cualquier par de puntos, la única posibilidad es que

- donde es posible que la cantidad escalar ω sea nula, en los casos de reposo o traslación. Esto permite tratar a la velocidad angular como una cantidad escalar, puesto que su dirección es conocida. El sentido de la velocidad angular lo da el signo de la cantidad escalar ω.
- 5) La aceleración angular del movimiento es perpendicular al plano director
Es consecuencia inmediata de que la velocidad angular posea dirección constante
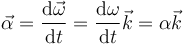
- 6) Son compatibles con un movimiento plano los movimientos instantáneos {21} de reposo, traslación o rotación, pero no el helicoidal
- Si
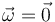 entonces el movimiento {21} es un estado de reposo o es una traslación.
entonces el movimiento {21} es un estado de reposo o es una traslación.
- Si la velocidad angular no es nula, la velocidad de deslizamiento vale 0
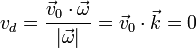
- y por tanto en ese caso el movimiento es una rotación.
- Cabe señalar que el movimiento plano más frecuente es una sucesión de rotaciones instantáneas, a veces con algún instante aislado de traslación o reposo. No obstante, son también destacables por su importancia los siguientes dos casos particulares de movimiento plano: la traslación permanente paralela a un plano fijo, y la rotación alrededor de un eje fijo.
- 7) Las distribuciones de velocidades en planos paralelos al plano director son idénticas entre sí
- Si el movimiento es una traslación, evidentemente las distribuciones son idénticas, ya que todos los puntos tienen la misma velocidad.
- Si se trata de una rotación, el eje instantáneo de rotación es perpendicular al plano director, y por tanto, las distribuciones de las velocidades en planos perpendiculares a este eje (y paralelos al plano director) son idénticas.
- Esto quiere decir que para estudiar el movimiento plano basta con considerar lo que ocurre en uno de sus planos paralelos al plano director. Esto no implica que el sólido sea cilíndrico (esto es, que el sólido real no tiene por qué tener la misma forma en todos los planos paralelos al director).
- 8) Las distribuciones de aceleraciones en planos paralelos al plano director son idénticas entre sí
- Si tenemos puntos P y Q situados sobre la misma recta normal al plano director,
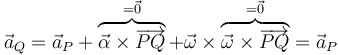
- 9) Un movimiento plano tiene tres grados de libertad
- Un movimiento rígido general tiene 6 grados de libertad, especificados por las tres componentes de la velocidad angular y las tres componentes de la velocidad de un punto. En un movimiento plano, la velocidad de cada punto se puede escribir
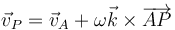
- donde
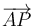 es el vector de posición relativa de un punto del plano director en el que se encuentra el origen de coordenadas. Gráficamente, el vector
es el vector de posición relativa de un punto del plano director en el que se encuentra el origen de coordenadas. Gráficamente, el vector 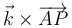 representa un giro del vector
representa un giro del vector 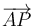 un ángulo de π / 2 en sentido antihorario dentro del plano director. La velocidad angular tiene una sola componente que puede variar, la normal al plano, y la velocidad de un punto tiene dos, tangentes al mismo plano
un ángulo de π / 2 en sentido antihorario dentro del plano director. La velocidad angular tiene una sola componente que puede variar, la normal al plano, y la velocidad de un punto tiene dos, tangentes al mismo plano
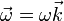
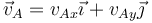
- Las especificación de esos 3 valores determina completamente el movimiento del sólido, que por tanto tiene 3 grados de libertad.
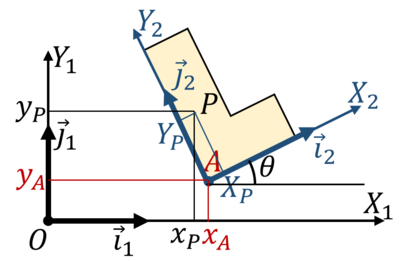
- Si ligamos un sistema de referencia al sólido que efectúa el movimiento plano, podemos usar como coordenadas para decribir su movimiento las coordenadas cartesianas de su origen xA, yA, y el ángulo θ que el eje OX2 forma con el OX1, cumpliéndose
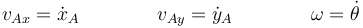
- 10) El eje instantáneo de rotación corta al plano director en un solo punto
- Es consecuencia inmediata de que el EIR, caso de existir, sea perpendicular a los planos directores. El punto de corte se denomina centro instantáneo de rotación (CIR). Para localizarlo basta con aplicar la fórmula general de cálculo del EIR y buscar su intersección con el plano director (situado habitualmente en z = 0).
- Consideremos, por ejemplo, el caso de un disco “2” que rueda sin deslizar sobre una superficie horizontal “1”. Es éste un movimiento plano, siendo el plano director uno normal a la superficie horizontal y paralelo a la superficie del disco. El EIR del movimiento {21} es una recta tangente al plano horizontal y que pasa por el punto de contacto del disco con el suelo. El CIR I21 en cada instante será el punto de contacto del disco con el suelo. Sin embargo, no hay ningún átomo del disco ni del suelo que coincida en todo momento con el CIR, sino que es uno diferente en cada instante.
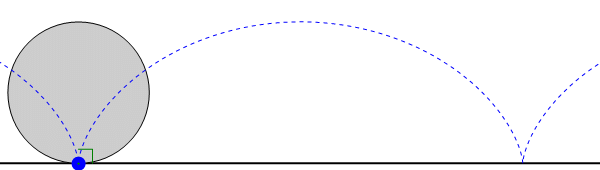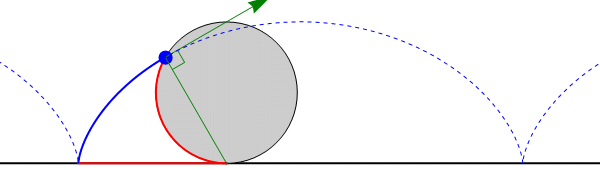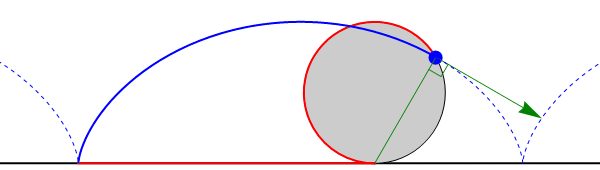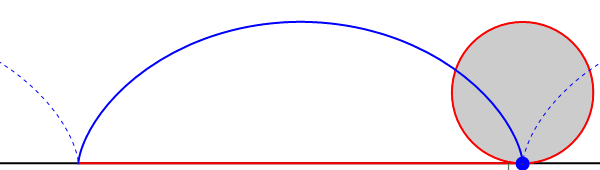
- En el caso de un movimiento de traslación, el centro instantáneo de rotación no corresponde a ningún punto del espacio, ya que no hay eje instantáneo de rotación. No obstante, puede considerarse un movimiento de traslación como un límite de movimientos de rotación con radios cada vez más grandes. Definiendo el CIR para un movimiento de traslación según este criterio, se encontraría en un punto del infinito, en la dirección dada por la perpendicular a la velocidad instantánea de traslación.
3 Expresión en el plano director
3.1 Posición
Una posible expresión de la posición instantánea de cualquier partícula consiste en dar la posición de un punto de referencia más la posición respecto al sistema ligado, que es siempre constante
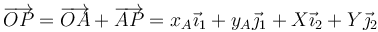
A su vez, los ejes ligados, en un movimiento plano, se relacionan con los fijos con una rotación en torno al eje OZ

lo que nos da las componentes
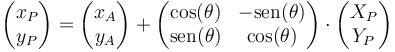
Vemos que la posición viene dada por tres coordenadas {xA,yA,θ}, como corresponde a que el sistema tiene tres grados de libertad.
3.2 Velocidad
La velocidad del punto P, por la expresión del campo de velocidades
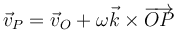
Dado un vector 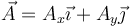 el producto
el producto
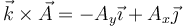
es un vector del mismo módulo que A ⃗, girado 90° respecto al original. Por ello, la velocidad de cada punto se compone de la velocidad del origen sumada a un vector ortogonal a la posición relativa. Separando por componentes
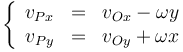
Nótese (otra vez) que O es un punto fijo, el origen de coordenadas, pero aun así su velocidad, en cuanto punto del sólido, es distinta de cero. A su vez, la velocidad angular en un movimiento plano se relaciona directamente con la variación del ángulo entre el sistema fijo y el ligado
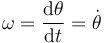
3.3 Aceleración
El campo de aceleraciones puede simplificarse en el caso del movimiento plano a la expresión
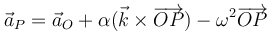
Separando por componentes
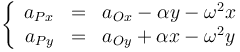
siendo la aceleración angular
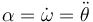
4 Centro instantáneo de rotación
4.1 Definición
En el caso de que el movimiento del sólido respecto al sistema fijo consista en una rotación, se define el centro instantáneo de rotación (CIR) del movimiento plano I, como el punto de intersección del eje instantáneo de rotación con el plano director de dicho movimiento. Hay que destacar que, en general, el CIR representa un punto material del sólido diferente en cada instante. Lo mismo ocurre con el sistema fijo: el CIR I coincide con un punto del espacio diferente en cada instante. Consideremos, por ejemplo, el caso de un disco “2” que rueda sin deslizar sobre una superficie horizontal “1”. Es éste un movimiento plano, siendo el plano director uno normal a la superficie horizontal y paralelo a la superficie del disco. El EIR del movimiento es una recta tangente al plano horizontal y que pasa por el punto de contacto del disco con el suelo. El CIR I en cada instante será el punto de contacto del disco con el suelo. Sin embargo, no hay ningún átomo del disco ni del suelo que coincida en todo momento con el CIR, sino que es uno diferente en cada instante. En el caso de un movimiento de traslación, el centro instantáneo de rotación no corresponde a ningún punto del espacio, ya que no hay eje instantáneo de rotación. No obstante, puede considerarse un movimiento de traslación como un límite de movimientos de rotación con radios cada vez más grandes. Definiendo el CIR para un movimiento de traslación según este criterio, se encontraría en un punto del infinito, en la dirección dada por la perpendicular a la velocidad instantánea de traslación.
En cada instante se cumple
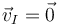
Esto no quiere decir que el punto I sea estacionario (ya que es uno distinto en cada instante) ni que la aceleración sea nula
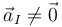
Puesto que I corresponde a un punto material distinto en cada instante, el valor de su velocidad no puede derivarse para obtener la aceleración. Podremos obtener, eso sí, la aceleración del punto material correspondiente empleando la expresión general del campo de aceleraciones. Así, para el caso de una rueda, la aceleración del punto de contacto con el suelo es radial y dirigida hacia el centro del disco. La distribución de velocidades posee simetría rotacional alrededor del CIR. De nuevo, es consecuencia de que se encuentre en el EIR:
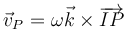
4.2 Localización del CIR
4.2.1 Procedimiento analítico
En el caso de una rotación, la posición del CIR de un movimiento puede hallarse analíticamente particularizando la fórmula de cálculo del EIRMD. Si A es un punto del plano director, con velocidad 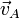 , y
, y  es la velocidad angular del movimiento, la posición relativa del CIR es
es la velocidad angular del movimiento, la posición relativa del CIR es
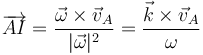
Vemos que efectivamente, cuando 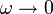 y el movimiento se reduce a una traslación, la posición del CIR se va al infinito según una dirección perpendicular a la velocidad de traslación.
y el movimiento se reduce a una traslación, la posición del CIR se va al infinito según una dirección perpendicular a la velocidad de traslación.
Si no se conoce la velocidad angular, sino la velocidad de dos puntos A y B del mismo plano director, puede hallarse previamente la velocidad angular a partir de la relación general
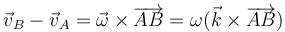
4.2.2 Procedimiento geométrico o gráfico
La posición del CIR también puede hallarse de forma sencilla geométricamente (teniendo el procedimiento geométrico su correspondiente versión analítica).
Suponemos que conocemos las velocidades de dos puntos del plano director, A y B. Clasificamos entonces el movimiento. Será una traslación si ambas velocidades son iguales y una rotación si son diferentes.
- Caso de una traslación
- Tomamos un punto cualquiera A, y trazamos la recta que pasa por A y es perpendicular a la velocidad
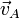 . El CIR I se encontrará en el infinito según la dirección de esta recta (equivalentemente en cualquiera de sus dos “extremos”).
. El CIR I se encontrará en el infinito según la dirección de esta recta (equivalentemente en cualquiera de sus dos “extremos”).
- Caso de una rotación con
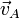 y
y 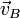 no paralelas
no paralelas - El CIR I se encuentra en la intersección de la recta que pasa por A y es perpendicular a
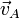 con la recta que pasa por B y es perpendicular a
con la recta que pasa por B y es perpendicular a  .
.
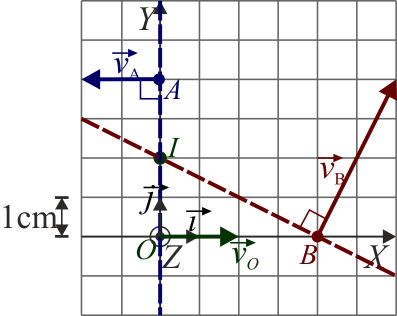
- Caso de una rotación con
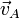 y
y 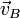 paralelas
paralelas - En ese caso el CIR se encuentra en la recta que une los puntos A y B. Para hallar la posición sobre esta recta, observamos que la velocidad de diferentes puntos en una rotación es proporcional a la distancia al eje. Por tanto si sobre la gráfica trazamos con la misma escala la velocidad
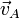 con origen en A, y la velocidad
con origen en A, y la velocidad 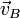 con origen en B, y trazamos la recta que pasa por los extremos de estos dos vectores, el punto donde corta a la recta AB es el CIR I.
con origen en B, y trazamos la recta que pasa por los extremos de estos dos vectores, el punto donde corta a la recta AB es el CIR I.