Movimiento general de un sólido rígido

De Laplace

Contenido

1 Movimientos finitos
2 Campo de velocidades

1 Movimientos finitos

El caso general de movimiento de un sólido es una composición de una rotaci´´on seguida de una traslación (o viceversa).

El procedimiento es simple. Elegimos un punto $O 0$ del sólido y efectuamos una rotación alrededor del punto hasta que la orientación del sólido coincide con la del estado final. A continuación trasladamos el sólido hasta que coincide con su ubicación definitiva.

En forma vectorial, es movimiento para cada punto será

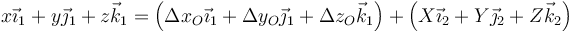
$x\vec{\imath}_1+y\vec{\jmath}_1+z\vec{k}_1=\left(\Delta x_O\vec{\imath}_1+\Delta y_O\vec{\jmath}_1+\Delta z_O\vec{k}_1\right)+\left(X\vec{\imath}_2+Y\vec{\jmath}_2+Z\vec{k}_2\right)$

o, en forma matricial

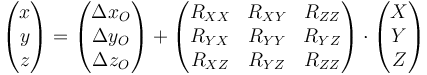
$\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}\Delta x_O\\ \Delta y_O\\ \Delta z_O\end{pmatrix}+\begin{pmatrix} R_{XX} & R_{XY} & R_{ZZ} \\ R_{YX} & R_{YY} & R_{YZ} \\ R_{XZ} & R_{YZ} & R_{ZZ} \end{pmatrix}\cdot \begin{pmatrix}X \\ Y \\ Z\end{pmatrix}$

El punto $O 0$ no tiene nada de particular. Podemos elegir cualquier otro punto para efectuar la rotación inicial. Dependiendo del punto que elijamos la traslación será diferente, pero la rotación será la misma sea cual sea el centro de reducción.

Chasles generalizó el teorema de Euler, observando que ese desplzamiento arbitrario puede descomponerse en una traslación paralela al eje de rotación y en una ortogonal a él. la parte ortogonal puede englobarse en la rotación, quedando solo la paralela.

Por tanto, el movimiento general de un sólido se reduce a una rotación en torno a un eje y un desplazamiento en la dirección de este eje (que en este contexto se denomina eje de rotación y mínimo deslizamiento). Este movimiento se denomina “un tornillo” por su analogía con la conducta de esta herramienta.

2 Campo de velocidades

Cuando un sólido rígido se mueve efectúa en cada instante un movimiento rígido infinitesimal.

Como en los movimientos finitos, consideraremos dos sistemas de referencia: el 1, que consideramos como fijo y el 2, ligado al sólido.

De acuerdo con el teorema de Chasles, este movimiento instantáneo se compondrá de una rotación diferencial alrededor de un eje (que ahora será eje instantáneo de rotación y mínimo deslizamiento, ya que puede cambiar de un instante a otro) y de un desplazamiento.

Si tomamos como referencia el punto O (“centro de reducción”) la velocidad de cualquier punto será la suma vectorial de la traslación de O más la rotación alrededor de un eje que pasa por O.

El desplazamiento de cada punto será la suma vectorial del correspondiente a la traslación más el debido a la rotación. Dividiendo por el intervalo $d t$ obtenemos la expresión general del campo de velocidades

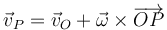
$\vec{v}_P=\vec{v}_O+\vec{\omega}\times\overrightarrow{OP}$

Aquí al vector $\vec{\omega}$ se lo denomina vector rotación del sólido o velocidad angular instantánea del sólido.

2.1 Cambio del centro de reducción

En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos

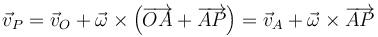
$\vec{v}_P=\vec{v}_O+\vec{\omega}\times\left(\overrightarrow{OA}+\overrightarrow{AP}\right)=\vec{v}_A+\vec{\omega}\times\overrightarrow{AP}$

es, decir, para cualquier par de puntos se cumple

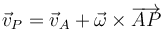
$\vec{v}_P=\vec{v}_A+\vec{\omega}\times\overrightarrow{AP}$

o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par 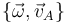$\{\vec{\omega},\vec{v}_A\}$ se lo denomina reducción cinemática del campo de velocidades en el punto A.

2.2 Invariantes

Hay dos cantidades que son iguales para todos los puntos del sólido:

Velocidad angular: Es el invariante vectoral $\vec{\omega}$ que, como hemos visto aparece en cualquier reducción cinemática. Es decir que cualquiera que sea el punto de referencia que tomemos, vemos al sólido girar instantáneamente con la misma velocidad angular.

Velocidad de deslizamiento: Es el invariante escalar. Si calculamos la componente de la velocidad de cada punto en la dirección de la velocidad angular tenemos

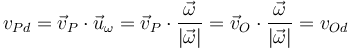
$v_{Pd}=\vec{v}_P\cdot\vec{u}_\omega=\vec{v}_P\cdot\frac{\vec{\omega}}{|\vec{\omega}|} = \vec{v}_O\cdot\frac{\vec{\omega}}{|\vec{\omega}|}=v_{Od}$

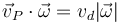Atendiendo a estas dos cantidades, o para evitar divisiones por cero, a $\vec{\omega}$ y $\vec{v}_P\cdot\vec{\omega}=v_d|\vec{\omega}|$ tenemos los siguientes posibles estados de movimiento: reposo, traslación, rotación y movimiento helicoidal.

2.3 Clasificación de movimientos

2.3.1 Reposo y traslación

Si la velocidad angular es nula en un instante dado, la velocidad de todos los puntos del sólido es idéntica en dicho instante.

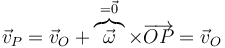
$\vec{v}_P=\vec{v}_O+\overbrace{\vec{\omega}}^{=\vec{0}}\times\overrightarrow{OP}=\vec{v}_O$

En particular, si un punto tiene velocidad nula, todos tienen velocidad nula. Se dice entonces que el sólido está en un estado de reposo, que puede ser instantáneo o permanente.

Si la velocidad de un punto (y, por tanto, de todos) no es nula, se dice que estamos en una traslación.

Si fijamos un sistema de ejes al sólido, estos mantienen su orientación en un movimiento de traslación.

Equivalentemente, el movimiento de traslación se puede enunciar afirmando que si tres puntos no colineales del sólido tienen la misma velocidad, todos los demás también tienen la misma.

Hay que insistir en que hablamos de velocidades instantáneas y del movimiento relativo de los diferentes puntos del sólido. Un movimiento de traslación NO significa que el sólido se mueve en línea recta, o a velocidad constante.

En el caso más restrictivo

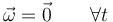
$\vec{\omega}=\vec{0} \qquad \forall t$

implica un movimiento de traslación permanente: los ejes ligados al sólido conservan su orientación en cada instante y el movimiento de cada uno de los puntos del sólido reproduce exactamente el de cualquier otro de ellos.

En una traslación permanente, la posición relativa de un punto cualquiera B respecto a otro punto arbitrario A se mantiene constante en módulo, dirección y sentido.

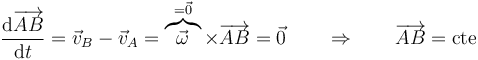
$\frac{\mathrm{d}\overrightarrow{AB}}{\mathrm{d}t}=\vec{v}_B-\vec{v}_A=\overbrace{\vec{\omega}}^{=\vec{0}}\times\overrightarrow{AB}= \vec{0}\qquad\Rightarrow\qquad \overrightarrow{AB}=\mathrm{cte}$

Un movimiento de traslación permanente no tiene por qué ser ni rectilíneo ni uniforme.

2.3.2 Movimiento de rotación y helicoidal

Si la velocidad angular es no nula, ya la velocidad no será la misma en todos los puntos. Atendiendo a la velocidad de deslizamiento, tenemos dos casos:

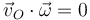
Movimiento de rotación: Si la velocidad de deslizamiento es nula, $v d = 0$ o, equivalentemente, si $\vec{v}_O\cdot\vec{\omega}= 0$

Movimiento helicoidal: Si la velocidad de deslizamiento es distinta de cero, 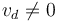$v_d\neq 0$ , o equivalentemente si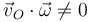 $\vec{v}_O\cdot\vec{\omega}\neq 0$

Estos dos movimientos comparten bastantes propiedades, y poseen algunas diferencias.

Si dos puntos están en una recta paralela a la velocidad angular, tienen la misma velocidad

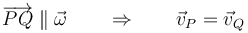
$\overrightarrow{PQ}\parallel \vec{\omega}\qquad\Rightarrow\qquad \vec{v}_P=\vec{v}_Q$

Esto permite reducir el estudio a lo que ocurre en planos perpendiculares a la velocidad angular, ya que la distribución de velocidades en estos planos paralelos será idéntica.

Inversamente, si dos puntos tienen la misma velocidad, la velocidad angular será paralela a la recta que pasa por estos dos puntos.

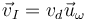
En cada uno de estos planos paralelos, existe un punto E cuya velocidad es la de deslizamiento (nula en el caso de rotación). Sea O el centro de reducción. Buscamos un punto I del plano normal a $\vec{\omega}$ y que pasa por O, tal que $\vec{v}_I=v_d\vec{u}_\omega$

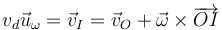
$v_d\vec{u}_\omega = \vec{v}_I=\vec{v}_O+\vec{\omega}\times\overrightarrow{OI}$

multiplicando aquí vectorialmente por $\vec{\omega}$ y aplicando las propiedades del doble producto vectorial

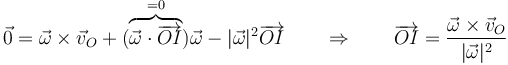
$\vec{0}=\vec{\omega}\times\vec{v}_O+(\overbrace{\vec{\omega}\cdot\overrightarrow{OI}}^{=0})\vec{\omega}-|\vec{\omega}|^2\overrightarrow{OI}\qquad\Rightarrow\qquad \overrightarrow{OI}=\frac{\vec{\omega}\times\vec{v}_O}{|\vec{\omega}|^2}$

Existe una recta de puntos que tienen como velocidad la de deslizamiento (nula, en el caso de la rotación). Estos puntos constituyen el eje instantáneo de rotación y mínimo deslizamiento (EIRMD), que se reduce al eje instantáneo de rotación (EIR) si la velocidad de deslizamiento es nula. Es consecuencia de las dos propiedades anteriores. Si la velocidad del punto I es la de deslizamiento, la de cualquier otro punto situado en la recta que pasa por I y en la dirección de laa velocidad angular tendrá la misma velocidad. La ecuación del eje será

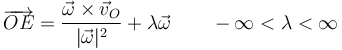
$\overrightarrow{OE}= \frac{\vec{\omega}\times\vec{v}_O}{|\vec{\omega}|^2}+\lambda\vec{\omega}\qquad -\infty<\lambda<\infty$

La velocidad de cualquier punto que no pertenezca al EIRMD tendrá una componente paralela al eje y una ortogonal a él

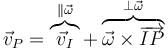
$\vec{v}_P=\overbrace{\vec{v}_I}^{\parallel \vec{\omega}}+\overbrace{\vec{\omega}\times\overrightarrow{IP}}^{\perp\vec{\omega}}$

La componente paralela es la velocidad de deslizamiento. La componente ortogonal representa la rotación en torno al EIRMD (EIR en su caso). Esta componente ortogonal está orientada según la regla de la mano derecha en torno al eje.

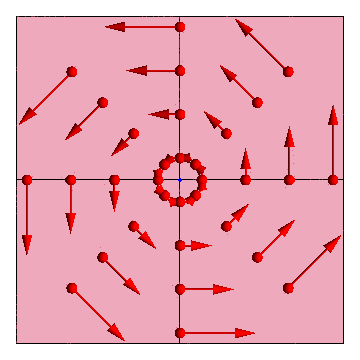
La rapidez de cada punto depende de la distancia al eje como

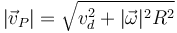
$|\vec{v}_P|=\sqrt{v_d^2+|\vec{\omega}|^2 R^2}$

siendo R la distancia del punto P al EIRMD. En el caso de una rotación (

v d = 0

) esta rapidez aumenta linealmente con la distancia al eje

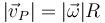
$|\vec{v}_P|=|\vec{\omega}| R$

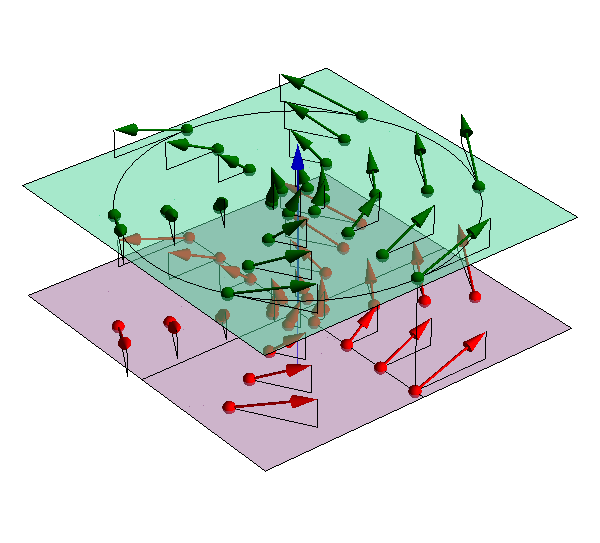
La estructura del campo de velocidades es entonces una combinación de avance a lo largo del EIRMD más una rotación en torno a éste.

Rotación	Helicoidal

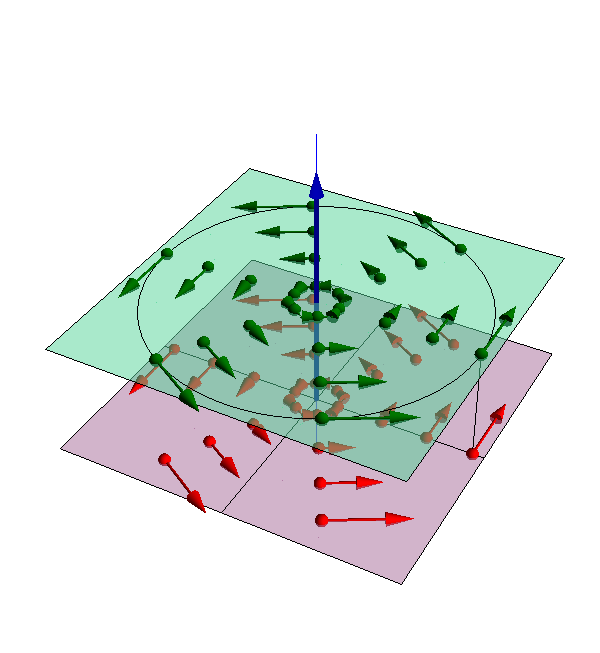
Esto nos permite caracterizar completamente el movimiento

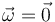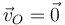Si $\vec{\omega}=\vec{0}$ y $\vec{v}_O=\vec{0}$ el estado es de reposo (instantáneo, en general).
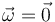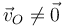Si $\vec{\omega}=\vec{0}$ y $\vec{v}_O\neq \vec{0}$ se trata de una traslación
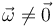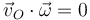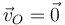Si $\vec{\omega}\neq\vec{0}$ y $\vec{v}_O\cdot\vec{\omega}=0$ (porque $\vec{v}_O=\vec{0}$ o es ortogonal a la velocidad angular) se trata de una rotación instantánea en torno a un EIR paralelo a la velocidad angular que pasa por 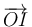$\overrightarrow{OI}$ (para el cual se anula la velocidad en ese caso).
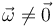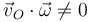Si $\vec{\omega}\neq\vec{0}$ y $\vec{v}_O\cdot\vec{\omega}\neq 0$ es un movimiento helicoidal instantáneo en torno a un EIRMD paralelo a la velocidad angular que pasa por 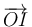$\overrightarrow{OI}$ (para el cual la velocidad vale 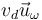$v_d\vec{u}_\omega$ y es paralela a la velocidad angular).

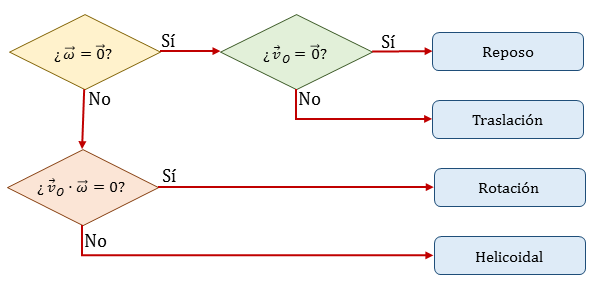
Al estudiar el movimiento de rotación y describir las velocidades según la ley se puede adquirir la idea errónea de que las partículas del sólido describen un movimiento circular. Eso NO es correcto. Lo que hemos hecho es describir la distribución instantánea de velocidades, esto es, qué velocidad tiene cada punto del sólido en un instante dado, pero no hemos analizado cómo se mueve cada punto a lo largo del tiempo (en términos llanos, hemos tomado una fotografía, no una película de vídeo).

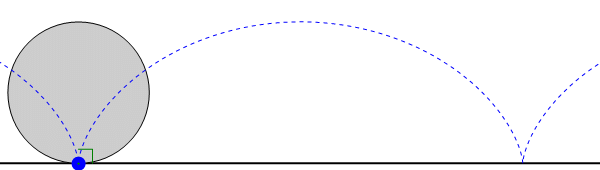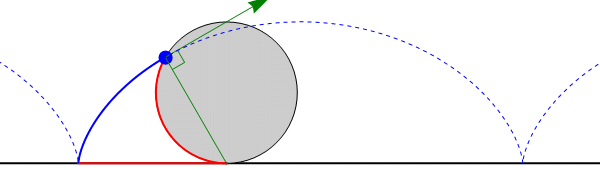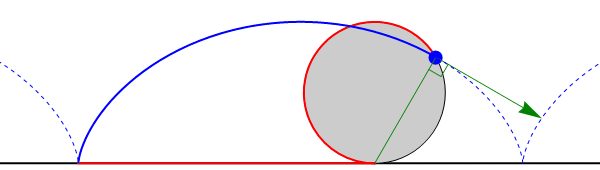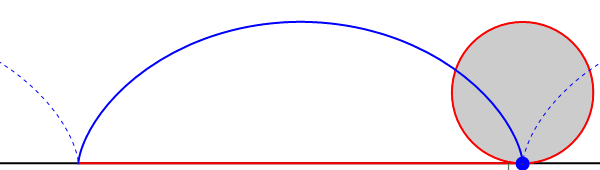
Consideremos el caso de un cilindro que rueda sobre el suelo. La línea de contacto esta formada por puntos con velocidad nula y por tanto se trata de un eje instantáneo de rotación. El cilindro está efectuando una rotación pura instantánea en torno a esta línea de contacto (y no respecto al eje del cilindro, como podría pensarse), pero la trayectoria de cada punto del cilindro no es una circunferencia, sino una cicloide (técnicamente, para los puntos que no son de la superficie exterior es una cicloide acortada).

La razón es que aunque instantáneamente esté rotando en torno a esta línea, el eje de rotación va cambiando en el tiempo.

Movimiento general de un sólido rígido

De Laplace

Contenido

1 Movimientos finitos

2 Campo de velocidades

2.1 Cambio del centro de reducción

2.2 Invariantes

2.3 Clasificación de movimientos

2.3.1 Reposo y traslación

2.3.2 Movimiento de rotación y helicoidal

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES