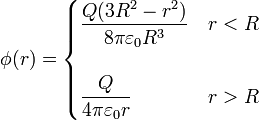Potencial en el centro de una esfera
De Laplace
(→Por integración directa) |
(→A partir del campo eléctrico) |
||
| (23 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
# en su volumen con una densidad <math>\rho = A r</math> (calcule previamente el valor de la constante <math>A</math>). | # en su volumen con una densidad <math>\rho = A r</math> (calcule previamente el valor de la constante <math>A</math>). | ||
| - | + | ==Esfera cargada uniformemente en la superficie== | |
| - | + | ||
En este caso de una carga en el centro de una esfera, la simetría del problema permite hacer el cálculo de forma sencilla tanto por integración directa como a partir del campo eléctrico. | En este caso de una carga en el centro de una esfera, la simetría del problema permite hacer el cálculo de forma sencilla tanto por integración directa como a partir del campo eléctrico. | ||
| - | + | ===Por integración directa=== | |
La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es | La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es | ||
| Línea 17: | Línea 16: | ||
En nuestro caso la superficie de integración es la esfera de radio <math>R</math>, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello | En nuestro caso la superficie de integración es la esfera de radio <math>R</math>, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello | ||
| - | <center><math>\sigma_s = \sigma_0 = \frac{Q}{4\pi R^2}</math>{{qquad}}<math>\mathbf{r} = \mathbf{0}</math>{{qquad}}<math>\mathbf{r'} = R\mathbf{u}_{r'}</math>{{qquad}} <math>|\mathbf{r}-\mathbf{r}'|=R | + | <center><math>\sigma_s = \sigma_0 = \frac{Q}{4\pi R^2}</math>{{qquad}}<math>\mathbf{r} = \mathbf{0}</math>{{qquad}}<math>\mathbf{r'} = R\mathbf{u}_{r'}</math>{{qquad}} <math>|\mathbf{r}-\mathbf{r}'|=R</math></center> |
Sustituyendo todo esto nos queda | Sustituyendo todo esto nos queda | ||
| Línea 25: | Línea 24: | ||
El resultado es un potencial análogo al que crearía una carga puntual situada a una distancia <math>R</math>. La razón es evidente: el centro de la esfera se encuentra a la misma distancia de todos los puntos de la superficie. Por tanto la contribución de cada elemento de superficie al potencial es simplemente la carga en dicho elemento dividida por la distancia, que es siempre la misma, y la constante <math>1/4\pi\varepsilon_0</math>. El resultado es la carga total dividida por <math>1/4\pi\varepsilon_0</math> y por <math>R</math>. | El resultado es un potencial análogo al que crearía una carga puntual situada a una distancia <math>R</math>. La razón es evidente: el centro de la esfera se encuentra a la misma distancia de todos los puntos de la superficie. Por tanto la contribución de cada elemento de superficie al potencial es simplemente la carga en dicho elemento dividida por la distancia, que es siempre la misma, y la constante <math>1/4\pi\varepsilon_0</math>. El resultado es la carga total dividida por <math>1/4\pi\varepsilon_0</math> y por <math>R</math>. | ||
| - | + | ===A partir del campo eléctrico=== | |
| + | Para hallar el potencial a partir del campo eléctrico, primero debemos conocer éste en todos los puntos del espacio, no solo en el origen. | ||
| - | ===Esfera cargada de forma no uniforme=== | + | Este cálculo se puede hacer por [[Campo_debido_a_una_superficie_esférica_cargada#Aplicando_las_leyes_de_la_electrostática|aplicación de la ley de Gauss]] o por [[Campo_debido_a_una_superficie_esférica_cargada#Por_integración_directa|integración directa]] y el resultado es |
| - | ===Esfera cargada uniformemente en el volumen==== | + | |
| - | ===Esfera cargada no uniformemente en el volumen | + | <center><math>\mathbf{E}=\begin{cases}\mathbf{0} & r < R \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & r > R\end{cases}</math></center> |
| + | |||
| + | esto es, el campo de una carga puntual en el exterior de la esfera, y un campo nulo en el interior de ella. | ||
| + | |||
| + | Para hallar el potencial en el centro de la esfera debemos calcular la integral desde el origen de potencial (situado en el infinito) hasta el punto donde queremos hallar el potencial (el origen de coordenadas), esto es | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = -\int_{\infty}^\mathbf{0}\mathbf{E}\cdot\mathrm{d}\mathbf{r}</math></center> | ||
| + | |||
| + | El resultado de esta integral es independiente del camino elegido, pero hay que elegir al menos uno. El más simple es uno rectilíneo radial, de forma que <math>\mathrm{d}\mathbf{r} = \mathrm{d}r\mathbf{u}_r</math>. | ||
| + | |||
| + | La integral de camino se compone de dos tramos, uno por el exterior y otro por el interior de la esfera | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = -\int_{\infty}^\mathbf{0}\mathbf{E}\cdot\mathrm{d}\mathbf{r}= \int_\infty^R \frac{Q\mathrm{d}r}{4\pi\varepsilon_0 r^2}+\int_R^0 0\,\mathrm{d}r = \frac{Q}{4\pi \varepsilon_0 R}</math></center> | ||
| + | |||
| + | que es por supuesto el mismo resultado que el obtenido anteriormente. Nótese que es muy importante incluir las dos contribuciones a la integral y no pensar que el potencial en el interior es solo la integral del campo en el interior. Puesto que el camino de integración viene desde el infinito, el exterior también debe contarse. | ||
| + | |||
| + | Este método de cálculo del potencial tiene la ventaja de que puede extenderse fácilmente a cualquier punto del espacio, no solo al centro de la esfera, mientras que la integración directa, aunque es factible, implica laboriosos cálculos. | ||
| + | |||
| + | Si este cálculo se aplica a otros valores de <math>r</math> el resultado es | ||
| + | |||
| + | <center><math>\phi(r)=\begin{cases}\displaystyle \frac{Q}{4\pi\varepsilon_0 R} & r < R \\ & \\ \displaystyle \frac{Q}{4\pi\varepsilon_0 r} & r > R\end{cases}</math></center> | ||
| + | |||
| + | ya que para todos los puntos del interior la segunda integral es nula, resultando un potencial uniforme. En los puntos del exterior tenemos la integral del campo de una carga puntual y el resultado es el potencial de una carga puntual. | ||
| + | |||
| + | ==Esfera cargada de forma no uniforme== | ||
| + | ===Por integración directa=== | ||
| + | [[Imagen:sigmacostheta.png|left]]Para el caso de una densidad de carga no uniforme, el procedimiento es exactamente el mismo que en el apartado anterior. De nuevo tenemos la misma posición de las cargas y la misma posición del punto donde queremos hallar el potencial. Por ello, volvemos a tener | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = \frac{Q}{4\pi\varepsilon_0 R}</math></center> | ||
| + | |||
| + | siendo <math>Q</math> la carga total de la superficie esférica que en este caso es | ||
| + | |||
| + | <center><math>Q = \int \sigma_s\,\mathrm{d}S' = \int_0^{2\pi}\int_0^\pi \sigma_0 \cos\theta' R^2 \,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi' = 2\pi R^2 \int_0^\pi \cos\theta'\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta' = 0</math></center> | ||
| + | |||
| + | La carga total es nula, como corresponde a que en esta distribución toda la carga en un hemisferio (el que va de 0 a <math>\pi/2</math>) es positiva, mientras que en el otro es igual y de signo contrario. Por tanto el potencial en el centro de la esfera es nulo. | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = \frac{Q}{4\pi\varepsilon_0 R}=0</math></center> | ||
| + | |||
| + | ===A partir del campo eléctrico=== | ||
| + | El cálculo del campo eléctrico producido en cualquier punto del espacio por una distribución de carga superficial <math>\sigma_s = \sigma_0\cos\theta</math> es un problema fácil de resolver por el método de separación de variables o por otros métodos alternativos. | ||
| + | |||
| + | Sin embargo, para calcular el potencial en el centro de la esfera no necesitamos conocer el campo en todos los puntos del espacio. Nos basta con aquellos puntos pertenecientes al camino de integración que hayamos elegido para ir desde el origen de potencial (el infinito) hasta el centro de la esfera. En este caso el camino más adecuado es uno rectilíneo a lo largo del plano ecuatorial de la esfera. La razón es clara atendiendo a la simetría de la distribución. | ||
| + | |||
| + | [[Imagen:doscargasplanoecuatorial.png|left]]Consideremos primero el caso de dos cargas puntuales iguales y opuestas separadas una distancia (un dipolo). El campo en el plano equidistante de las dos cargas es siempre perpendicular a dicho plano. | ||
| + | |||
| + | [[Imagen:distribucioncargasimetrica.png|right]]Por el principio de superposición, siempre que tengamos una distribución de carga simétrica respecto a un plano (como en el caso de la distribución que nos ocupa), el campo en este plano va a ser perpendicular a él. Si tomamos este plano ecuatorial como <math>z=0</math>, el campo tendrá la expresión | ||
| + | |||
| + | <center><math>\mathbf{E}(x,y,0) = E(x,y)\mathbf{u}_z</math></center> | ||
| + | |||
| + | Si ahora tomamos como camino de integración uno que vaya a lo largo de este plano (no necesariamente uno rectilíneo), se cumplirá para todos los puntos del camino de integración, que | ||
| + | |||
| + | <center><math>\mathbf{E}(x,y,0)\cdot\mathrm{d}\mathbf{r} = E(x,y)\mathbf{u}_z\cdot\mathrm{d}\mathbf{r}=0</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>\phi(x,y,0)= -\int_\infty^\mathbf{r} \mathbf{E}\cdot\mathrm{d}\mathbf{r} = 0</math></center> | ||
| + | |||
| + | esto es, el plano ecuatorial es un plano equipotencial cuyo potencial es igual a 0. En particular, se anula el potencial en el centro de la esfera. | ||
| + | |||
| + | ==Esfera cargada uniformemente en el volumen== | ||
| + | ===Por integración directa=== | ||
| + | La expresión integral para el potencial eléctrico debido a una distribución volumétrica de carga es | ||
| + | |||
| + | <center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int_\tau \frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'</math></center> | ||
| + | |||
| + | En nuestro caso el volumen de integración es la esfera de radio <math>R</math>, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello | ||
| + | |||
| + | <center><math>\rho = \rho_0 = \frac{Q}{4\pi R^3/3}</math>{{qquad}}<math>\mathbf{r} = \mathbf{0}</math>{{qquad}}<math>\mathbf{r'} = r'\mathbf{u}_{r'}</math>{{qquad}} <math>|\mathbf{r}-\mathbf{r}'|=r'</math></center> | ||
| + | |||
| + | Sustituyendo todo esto nos queda | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = \frac{1}{4\pi\varepsilon_0}\,\frac{3Q}{4\pi R^3}\int_0^R\int_\Omega \frac{r'^2\mathrm{d}\Omega'\,\mathrm{d}r'}{r'} = \frac{3Q}{8\pi\varepsilon_0 R}</math></center> | ||
| + | |||
| + | En esta integral hemos abreviado la expresión usando la definición de ángulo sólido | ||
| + | |||
| + | <center> | ||
| + | <math>\mathrm{d}\Omega' = \frac{\mathrm{d}S'}{r'^2} = \mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'</math>{{qquad}}<math>\int_\Omega\left(\dots\right)\,\mathrm{d}\Omega' = \int_0^{2\pi}\int_0^\pi \left(\dots\right)\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'</math></center> | ||
| + | |||
| + | Podemos llegar a este valor del potencial de forma más intuitiva empleando el resultado del primer apartado. La esfera maciza puede descomponerse en una serie de capas concéntricas, de radio <math>r'</math> y espesor <math>\mathrm{d}r'</math>, cada una de las cuales contribuye al potencial como | ||
| + | |||
| + | <center><math>\mathrm{d}\phi(\mathbf{0}) = \frac{\mathrm{d}Q}{4\pi\varepsilon_0 r'}</math></center> | ||
| + | |||
| + | siendo la carga en cada capa | ||
| + | |||
| + | <center><math>\mathrm{d}Q=\rho\,d\tau = \rho\,4\pi r'^2\,\mathrm{d}r'=\frac{3Q r'^2\,\mathrm{d}r'}{R^3}</math></center> | ||
| + | |||
| + | y el potencial total | ||
| + | |||
| + | <center><math> | ||
| + | \phi(\mathbf{0}) = \int_0^R \frac{3Qr'^2\,\mathrm{d}r'}{4\pi\varepsilon_0r'R^3} = \frac{3Q}{2\pi\varepsilon_0 R}</math></center> | ||
| + | |||
| + | ===A partir del campo eléctrico=== | ||
| + | Para hallar el potencial a partir del campo eléctrico, debemos conocer éste en todos los puntos del espacio por los que pase el camino de integración, que en este caso será una semirrecta desde el infinito hasta el centro de la esfera. | ||
| + | |||
| + | Para estos puntos el campo puede hallarse por [[Campo_debido_a_una_esfera_cargada_uniformemente|aplicación de la Ley de Gauss]], siendo su valor | ||
| + | |||
| + | <center><math>\mathbf{E}=\begin{cases}\displaystyle \frac{Qr\mathbf{u}_r}{4\pi\varepsilon_0 R^3} & r < R \\ & \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & r > R\end{cases}</math></center> | ||
| + | |||
| + | esto es, el campo de una carga puntual en el exterior de la esfera, y un campo que varía linealmente con la distancia, en el interior de ella. | ||
| + | |||
| + | Integrando a lo largo de la semirrecta, la integral de camino se compone de dos tramos, uno por el exterior y otro por el interior de la esfera | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = -\int_{\infty}^\mathbf{0}\mathbf{E}\cdot\mathrm{d}\mathbf{r}= \int_\infty^R \frac{Q\mathrm{d}r}{4\pi\varepsilon_0 r^2}+\int_R^0 \frac{Qr}{4\pi\varepsilon_0 R^3}\,\mathrm{d}r = \frac{Q}{4\pi \varepsilon_0 R}+\frac{Q}{8\pi \varepsilon_0 R}=\frac{3Q}{8\pi \varepsilon_0 R}</math></center> | ||
| + | |||
| + | Si este cálculo se aplica a otros valores de <math>r</math> el resultado es | ||
| + | |||
| + | <center><math>\phi(r)=\begin{cases}\displaystyle \frac{Q(3R^2-r^2)}{8\pi\varepsilon_0 R^3} & r < R \\ & \\ \displaystyle \frac{Q}{4\pi\varepsilon_0 r} & r > R\end{cases}</math></center> | ||
| + | |||
| + | ==Esfera cargada no uniformemente en el volumen== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 19:14 28 jun 2010
Contenido |
1 Enunciado
Calcule el potencial eléctrico en el centro de una esfera de radio R, cargada con una carga Q0 distribuida…
- uniformemente en su superficie
- de forma no uniforme en su superficie, con densidad σs = σ0cosθ.
- uniformemente en su volumen
- en su volumen con una densidad ρ = Ar (calcule previamente el valor de la constante A).
2 Esfera cargada uniformemente en la superficie
En este caso de una carga en el centro de una esfera, la simetría del problema permite hacer el cálculo de forma sencilla tanto por integración directa como a partir del campo eléctrico.
2.1 Por integración directa
La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es
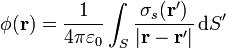
En nuestro caso la superficie de integración es la esfera de radio R, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello
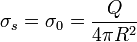
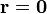
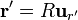
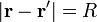
Sustituyendo todo esto nos queda
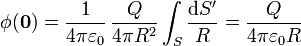
El resultado es un potencial análogo al que crearía una carga puntual situada a una distancia R. La razón es evidente: el centro de la esfera se encuentra a la misma distancia de todos los puntos de la superficie. Por tanto la contribución de cada elemento de superficie al potencial es simplemente la carga en dicho elemento dividida por la distancia, que es siempre la misma, y la constante 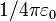 . El resultado es la carga total dividida por
. El resultado es la carga total dividida por 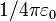 y por R.
y por R.
2.2 A partir del campo eléctrico
Para hallar el potencial a partir del campo eléctrico, primero debemos conocer éste en todos los puntos del espacio, no solo en el origen.
Este cálculo se puede hacer por aplicación de la ley de Gauss o por integración directa y el resultado es
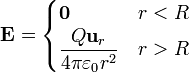
esto es, el campo de una carga puntual en el exterior de la esfera, y un campo nulo en el interior de ella.
Para hallar el potencial en el centro de la esfera debemos calcular la integral desde el origen de potencial (situado en el infinito) hasta el punto donde queremos hallar el potencial (el origen de coordenadas), esto es
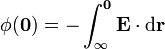
El resultado de esta integral es independiente del camino elegido, pero hay que elegir al menos uno. El más simple es uno rectilíneo radial, de forma que 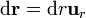 .
.
La integral de camino se compone de dos tramos, uno por el exterior y otro por el interior de la esfera
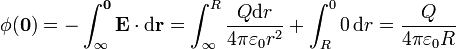
que es por supuesto el mismo resultado que el obtenido anteriormente. Nótese que es muy importante incluir las dos contribuciones a la integral y no pensar que el potencial en el interior es solo la integral del campo en el interior. Puesto que el camino de integración viene desde el infinito, el exterior también debe contarse.
Este método de cálculo del potencial tiene la ventaja de que puede extenderse fácilmente a cualquier punto del espacio, no solo al centro de la esfera, mientras que la integración directa, aunque es factible, implica laboriosos cálculos.
Si este cálculo se aplica a otros valores de r el resultado es
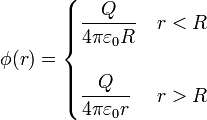
ya que para todos los puntos del interior la segunda integral es nula, resultando un potencial uniforme. En los puntos del exterior tenemos la integral del campo de una carga puntual y el resultado es el potencial de una carga puntual.
3 Esfera cargada de forma no uniforme
3.1 Por integración directa
Para el caso de una densidad de carga no uniforme, el procedimiento es exactamente el mismo que en el apartado anterior. De nuevo tenemos la misma posición de las cargas y la misma posición del punto donde queremos hallar el potencial. Por ello, volvemos a tener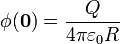
siendo Q la carga total de la superficie esférica que en este caso es
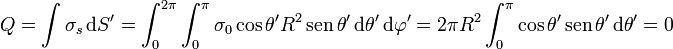
La carga total es nula, como corresponde a que en esta distribución toda la carga en un hemisferio (el que va de 0 a π / 2) es positiva, mientras que en el otro es igual y de signo contrario. Por tanto el potencial en el centro de la esfera es nulo.
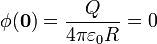
3.2 A partir del campo eléctrico
El cálculo del campo eléctrico producido en cualquier punto del espacio por una distribución de carga superficial σs = σ0cosθ es un problema fácil de resolver por el método de separación de variables o por otros métodos alternativos.
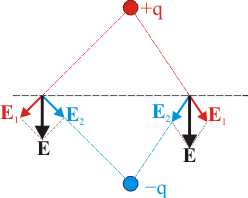
Sin embargo, para calcular el potencial en el centro de la esfera no necesitamos conocer el campo en todos los puntos del espacio. Nos basta con aquellos puntos pertenecientes al camino de integración que hayamos elegido para ir desde el origen de potencial (el infinito) hasta el centro de la esfera. En este caso el camino más adecuado es uno rectilíneo a lo largo del plano ecuatorial de la esfera. La razón es clara atendiendo a la simetría de la distribución.
Consideremos primero el caso de dos cargas puntuales iguales y opuestas separadas una distancia (un dipolo). El campo en el plano equidistante de las dos cargas es siempre perpendicular a dicho plano. Por el principio de superposición, siempre que tengamos una distribución de carga simétrica respecto a un plano (como en el caso de la distribución que nos ocupa), el campo en este plano va a ser perpendicular a él. Si tomamos este plano ecuatorial como z = 0, el campo tendrá la expresión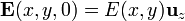
Si ahora tomamos como camino de integración uno que vaya a lo largo de este plano (no necesariamente uno rectilíneo), se cumplirá para todos los puntos del camino de integración, que
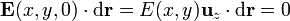
y por tanto
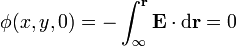
esto es, el plano ecuatorial es un plano equipotencial cuyo potencial es igual a 0. En particular, se anula el potencial en el centro de la esfera.
4 Esfera cargada uniformemente en el volumen
4.1 Por integración directa
La expresión integral para el potencial eléctrico debido a una distribución volumétrica de carga es
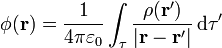
En nuestro caso el volumen de integración es la esfera de radio R, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello
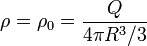
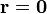
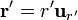
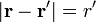
Sustituyendo todo esto nos queda
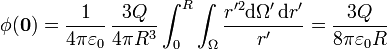
En esta integral hemos abreviado la expresión usando la definición de ángulo sólido
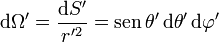
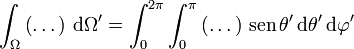
Podemos llegar a este valor del potencial de forma más intuitiva empleando el resultado del primer apartado. La esfera maciza puede descomponerse en una serie de capas concéntricas, de radio r' y espesor dr', cada una de las cuales contribuye al potencial como
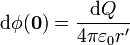
siendo la carga en cada capa
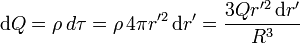
y el potencial total
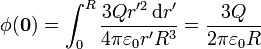
4.2 A partir del campo eléctrico
Para hallar el potencial a partir del campo eléctrico, debemos conocer éste en todos los puntos del espacio por los que pase el camino de integración, que en este caso será una semirrecta desde el infinito hasta el centro de la esfera.
Para estos puntos el campo puede hallarse por aplicación de la Ley de Gauss, siendo su valor
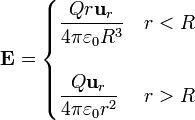
esto es, el campo de una carga puntual en el exterior de la esfera, y un campo que varía linealmente con la distancia, en el interior de ella.
Integrando a lo largo de la semirrecta, la integral de camino se compone de dos tramos, uno por el exterior y otro por el interior de la esfera
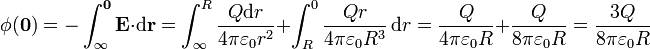
Si este cálculo se aplica a otros valores de r el resultado es