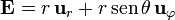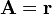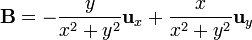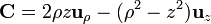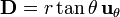Entrar Página Discusión Historial Go to the site toolbox

Campos vectoriales en diferentes sistemas

De Laplace

(Diferencias entre revisiones)
(→Cuarto campo)
(→Primer campo)
 
(7 ediciones intermedias no se muestran.)
Línea 7: Línea 7:
# <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math>
# <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math>
-
==Solución==
+
 
-
===Primer campo===
+
==Primer campo==
Para expresar el vector de posición en diferentes sistemas coordenados, lo más simple es aplicar que se trata de un gradiente, tal como se ve en [[cálculo de gradientes|otro problema]].
Para expresar el vector de posición en diferentes sistemas coordenados, lo más simple es aplicar que se trata de un gradiente, tal como se ve en [[cálculo de gradientes|otro problema]].
Línea 17: Línea 17:
A continuación, multiplicamos por cada uno de los vectores de la base, expresados también en sus componentes cartesianas. La componente radial es
A continuación, multiplicamos por cada uno de los vectores de la base, expresados también en sus componentes cartesianas. La componente radial es
-
<center><math>\mathbf{u}_{r}=\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\mathrm{sen}\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z}</math></center>
+
<center><math>\mathbf{u}_{r}=\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\mathrm{sen}\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z}</math>{{qquad}}{{qquad}}<math>\mathbf{r}{\cdot}\mathbf{u}_{r}=r(\mathrm{sen}^2\theta\cos^2\varphi+\mathrm{sen}^2\theta\mathrm{sen}^2\varphi+\cos^2\theta)=r</math></center>
-
 
+
-
 
+
-
<center><math>\mathbf{r}{\cdot}\mathbf{u}_{r}=r(\mathrm{sen}^2\theta\cos^2\varphi+\mathrm{sen}^2\theta\mathrm{sen}^2\varphi+\cos^2\theta)=r</math></center>
+
La componente polar se anula
La componente polar se anula
-
<center><math>\mathbf{u}_{\theta}=\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\mathrm{sen}\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z}</math></center>
+
<center><math>\mathbf{u}_{\theta}=\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\mathrm{sen}\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z}</math>{{qquad}}{{qquad}}<math>\mathbf{r}{\cdot}\mathbf{u}_{\theta}=r(\mathrm{sen}\,\theta\cos\theta\cos^2\varphi+\mathrm{sen}\,\theta\cos\theta\mathrm{sen}^2\varphi-\mathrm{sen}\,\theta\cos\theta)=0</math></center>
-
 
+
-
<center><math>\mathbf{r}{\cdot}\mathbf{u}_{\theta}=r(\mathrm{sen}\,\theta\cos\theta\cos^2\varphi+\mathrm{sen}\,\theta\cos\theta\mathrm{sen}^2\varphi-\mathrm{sen}\,\theta\cos\theta)=0</math></center>
+
Lo mismo ocurre con la componente acimutal
Lo mismo ocurre con la componente acimutal
-
<center><math>\mathbf{u}_{\varphi}=-\mathrm{sen}\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y}</math></center>
+
<center><math>\mathbf{u}_{\varphi}=-\mathrm{sen}\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y}</math>{{qquad}}{{qquad}}<math>\mathbf{r}{\cdot}\mathbf{u}_{\varphi}=r(-\mathrm{sen}\,\theta\cos\varphi\mathrm{sen}\varphi+\mathrm{sen}\,\theta\mathrm{sen}\varphi\cos\varphi)=0</math></center>
-
 
+
-
 
+
-
<center><math>\mathbf{r}{\cdot}\mathbf{u}_{\varphi}=r(-\mathrm{sen}\,\theta\cos\varphi\mathrm{sen}\varphi+\mathrm{sen}\,\theta\mathrm{sen}\varphi\cos\varphi)=0</math></center>
+
por lo que la expresión final es el conocido
por lo que la expresión final es el conocido
Línea 45: Línea 37:
Operando después con los coeficientes de cada vector de la base esférica se llega a la expresión buscada.
Operando después con los coeficientes de cada vector de la base esférica se llega a la expresión buscada.
-
===Segundo campo===
+
==Segundo campo==
Para el campo
Para el campo
Línea 72: Línea 64:
<center><math>\mathbf{B}=\frac{1}{r\mathrm{sen}\theta}\mathbf{u}_{\varphi}</math></center>
<center><math>\mathbf{B}=\frac{1}{r\mathrm{sen}\theta}\mathbf{u}_{\varphi}</math></center>
-
===Tercer campo===
+
==Tercer campo==
Para poner este vector en cartesianas tenemos que
Para poner este vector en cartesianas tenemos que
Línea 89: Línea 81:
<math>=r^2\cos\theta\mathbf{u}_{r}+r^2\mathrm{sen}\,\theta\mathbf{u}_{\theta}</math></center>
<math>=r^2\cos\theta\mathbf{u}_{r}+r^2\mathrm{sen}\,\theta\mathbf{u}_{\theta}</math></center>
-
===Cuarto campo===
+
==Cuarto campo==
Si aplicamos la relación del vector <math>\mathbf{u}_{\theta}</math> con los unitarios de cartesianas tenemos
Si aplicamos la relación del vector <math>\mathbf{u}_{\theta}</math> con los unitarios de cartesianas tenemos
<center><math>\mathbf{D}=r\tan\theta\mathbf{u}_{\theta}=
<center><math>\mathbf{D}=r\tan\theta\mathbf{u}_{\theta}=
-
r\tan\theta(\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z})=</math>
+
r\tan\theta(\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z})=</math></center>
-
<math>=r\,\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+r\,\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-r\frac{\mathrm{sen}^2\theta}{\cos\theta}\mathbf{u}_{z}</math></center>
+
 
 +
<center><math>=r\,\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+r\,\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-r\frac{\mathrm{sen}^2\theta}{\cos\theta}\mathbf{u}_{z}</math></center>
las dos primeras componentes se reconocen como
las dos primeras componentes se reconocen como
Línea 117: Línea 110:
Aunque parece, a la vista de estos ejemplos, que cualquier campo se expresa de forma simple en los tres sistemas de coordenadas, no es en absoluto así. La mayoría de los campos que poseen una expresión simple en un sistema, pueden ser tremendamente complejos en los otros dos.
Aunque parece, a la vista de estos ejemplos, que cualquier campo se expresa de forma simple en los tres sistemas de coordenadas, no es en absoluto así. La mayoría de los campos que poseen una expresión simple en un sistema, pueden ser tremendamente complejos en los otros dos.
-
===Quinto campo===
+
==Quinto campo==
Para el campo
Para el campo
Línea 126: Línea 119:
<center><math>\mathbf{E} = \left(x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}\right)+\left(-y\mathbf{u}_{x}+x\mathbf{u}_y\right)\,</math></center>
<center><math>\mathbf{E} = \left(x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}\right)+\left(-y\mathbf{u}_{x}+x\mathbf{u}_y\right)\,</math></center>
-
El primer sumando es el vector de posición, estudiado en el [[#Primer campo|primer caso]] mientras que el segundo sumando es igual al [[#Segundo campo]] multiplicado por <math>x^2+y^2 = \rho^2</math>:
+
El primer sumando es el vector de posición, estudiado en el [[#Primer campo|primer caso]] mientras que el segundo sumando es igual al [[#Segundo campo|segundo campo]] multiplicado por <math>x^2+y^2 = \rho^2</math>:
-
<center><math>\-y\mathbf{u}_x+x\mathbf{u}_y = \rho\,\mathbf{u}_\varphi = r\,\mathrm{sen}\,\theta\mathbf{u}_\varphi</math></center>
+
<center><math>-y\mathbf{u}_x+x\mathbf{u}_y = \rho\,\mathbf{u}_\varphi = r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi</math></center>
Por tanto, el campo <math>\mathbf{E}</math> se escribirá en cilíndricas
Por tanto, el campo <math>\mathbf{E}</math> se escribirá en cilíndricas
Línea 137: Línea 130:
<center><math>\mathbf{E} = r\,\mathbf{u}_r + r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi</math></center>
<center><math>\mathbf{E} = r\,\mathbf{u}_r + r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi</math></center>
-
 
[[Categoría:Problemas de fundamentos matemáticos]]
[[Categoría:Problemas de fundamentos matemáticos]]

última version al 13:33 3 abr 2009

Contenido

1 Enunciado

Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:

  1. \mathbf{A} = \mathbf{r}\,
  2. \mathbf{B} = -\dfrac{y}{x^2+y^2}\mathbf{u}_{x}+\dfrac{x}{x^2+y^2}\mathbf{u}_{y}
  3. \mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}
  4. \mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}


2 Primer campo

Para expresar el vector de posición en diferentes sistemas coordenados, lo más simple es aplicar que se trata de un gradiente, tal como se ve en otro problema.

Otra posibilidad es el cálculo directo. Por ejemplo, para expresar este vector en coordenadas esféricas, escribimos en primer lugar las componentes cartesianas en función de las coordenadas esféricas

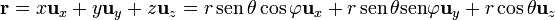
\mathbf{r}=x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}=r\,\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+r\,\mathrm{sen}\,\theta\mathrm{sen}\varphi\mathbf{u}_{y}+r\cos\theta\mathbf{u}_{z}

A continuación, multiplicamos por cada uno de los vectores de la base, expresados también en sus componentes cartesianas. La componente radial es

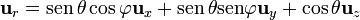
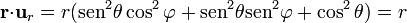
\mathbf{u}_{r}=\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\mathrm{sen}\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z}        \mathbf{r}{\cdot}\mathbf{u}_{r}=r(\mathrm{sen}^2\theta\cos^2\varphi+\mathrm{sen}^2\theta\mathrm{sen}^2\varphi+\cos^2\theta)=r

La componente polar se anula

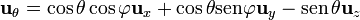
\mathbf{u}_{\theta}=\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\mathrm{sen}\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z}        \mathbf{r}{\cdot}\mathbf{u}_{\theta}=r(\mathrm{sen}\,\theta\cos\theta\cos^2\varphi+\mathrm{sen}\,\theta\cos\theta\mathrm{sen}^2\varphi-\mathrm{sen}\,\theta\cos\theta)=0

Lo mismo ocurre con la componente acimutal

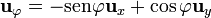
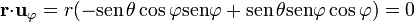
\mathbf{u}_{\varphi}=-\mathrm{sen}\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y}        \mathbf{r}{\cdot}\mathbf{u}_{\varphi}=r(-\mathrm{sen}\,\theta\cos\varphi\mathrm{sen}\varphi+\mathrm{sen}\,\theta\mathrm{sen}\varphi\cos\varphi)=0

por lo que la expresión final es el conocido

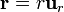
\mathbf{r}=r\mathbf{u}_{r}

Una posibilidad adicional de cálculo directo consiste en, tras sustituir las componentes cartesianas por su expresión esféricas, expresar los vectores de la base cartesiana como combinación lineal de los vectores de la base en esféricas. Así, por ejemplo,

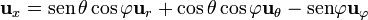
\mathbf{u}_{x}=\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{r}+\cos\theta\cos\varphi\mathbf{u}_{\theta}-\mathrm{sen}\varphi\mathbf{u}_{\varphi}

Operando después con los coeficientes de cada vector de la base esférica se llega a la expresión buscada.

3 Segundo campo

Para el campo

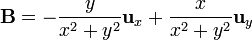
\mathbf{B}=-\frac{y}{x^2+y^2}\mathbf{u}_{x}+\frac{x}{x^2+y^2}\mathbf{u}_{y}

podemos sustituir la definición de las coordenadas cilíndricas

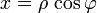
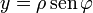
x=\rho\,\cos\varphi    y=\rho\,\mathrm{sen}\,\varphi    z=z\,

y obtener

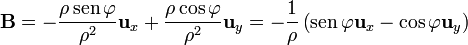
\mathbf{B}=-\frac{\rho\,\mathrm{sen}\,\varphi}{\rho^2}\mathbf{u}_{x}+ \frac{\rho\cos\varphi}{\rho^2}\mathbf{u}_{y} =-\frac{1}{\rho}\left(\mathrm{sen}\,\varphi\mathbf{u}_{x}-\cos\varphi\mathbf{u}_{y}\right)

el vector que aparece entre paréntesis no es otro que 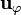\mathbf{u}_{\varphi} por lo que

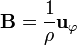
\mathbf{B}=\frac{1}{\rho}\mathbf{u}_{\varphi}

En esféricas tenemos que, dado que

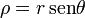
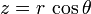
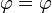
\rho=r\,\mathrm{sen}\theta    z=r\,\cos\theta    \varphi=\varphi

y que 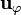\mathbf{u}_{\varphi} es el mismo en los dos sistemas,

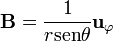
\mathbf{B}=\frac{1}{r\mathrm{sen}\theta}\mathbf{u}_{\varphi}

4 Tercer campo

Para poner este vector en cartesianas tenemos que

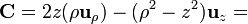
\mathbf{C}=2z(\rho\mathbf{u}_{\rho})-(\rho^2-z^2)\mathbf{u}_{z}=

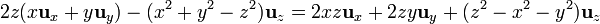
2z(x\mathbf{u}_{x}+y\mathbf{u}_{y})-(x^2+y^2-z^2)\mathbf{u}_{z}=2xz\mathbf{u}_{x}+2zy\mathbf{u}_{y}+ (z^2-x^2-y^2)\mathbf{u}_{z}

y para pasarlo a esféricas resulta

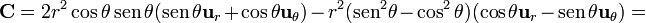
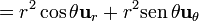
\mathbf{C}=2r^2\cos\theta\,\mathrm{sen}\,\theta(\mathrm{sen}\,\theta\mathbf{u}_{r}+\cos\theta\mathbf{u}_{\theta})- r^2(\mathrm{sen}^2\theta-\cos^2\theta)(\cos\theta\mathbf{u}_{r}-\mathrm{sen}\,\theta\mathbf{u}_{\theta}) = =r^2\cos\theta\mathbf{u}_{r}+r^2\mathrm{sen}\,\theta\mathbf{u}_{\theta}

5 Cuarto campo

Si aplicamos la relación del vector 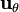\mathbf{u}_{\theta} con los unitarios de cartesianas tenemos

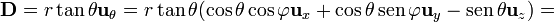
\mathbf{D}=r\tan\theta\mathbf{u}_{\theta}= r\tan\theta(\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z})=


=r\,\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+r\,\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{y}-r\frac{\mathrm{sen}^2\theta}{\cos\theta}\mathbf{u}_{z}

las dos primeras componentes se reconocen como

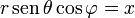
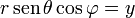
r\,\mathrm{sen}\,\theta\cos\varphi=x    r\,\mathrm{sen}\,\theta\cos\varphi=y

mientras que la tercera vale

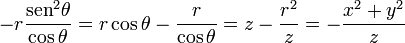
-r\frac{\mathrm{sen}^2\theta}{\cos\theta}=r\cos\theta-\frac{r}{\cos\theta}=z-\frac{r^2}{z}= -\frac{x^2+y^2}{z}

por lo que la expresión de \mathbf{D} es

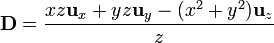
\mathbf{D}=\frac{xz\mathbf{u}_{x}+yz\mathbf{u}_{y}-(x^2+y^2)\mathbf{u}_{z}}{z}

De la expresión anterior es simple pasar a cilíndricas

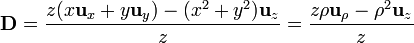
\mathbf{D}=\frac{z(x\mathbf{u}_{x}+y\mathbf{u}_{y})-(x^2+y^2)\mathbf{u}_{z}}{z}= \frac{z\rho\mathbf{u}_{\rho}-\rho^2\mathbf{u}_{z}}{z}

Aunque parece, a la vista de estos ejemplos, que cualquier campo se expresa de forma simple en los tres sistemas de coordenadas, no es en absoluto así. La mayoría de los campos que poseen una expresión simple en un sistema, pueden ser tremendamente complejos en los otros dos.

6 Quinto campo

Para el campo

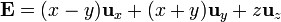
\mathbf{E} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}\,

simplemente lo descomponemos en suma de dos

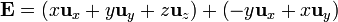
\mathbf{E} = \left(x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}\right)+\left(-y\mathbf{u}_{x}+x\mathbf{u}_y\right)\,

El primer sumando es el vector de posición, estudiado en el primer caso mientras que el segundo sumando es igual al segundo campo multiplicado por x2 + y2 = ρ2:

-y\mathbf{u}_x+x\mathbf{u}_y = \rho\,\mathbf{u}_\varphi = r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi

Por tanto, el campo \mathbf{E} se escribirá en cilíndricas

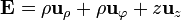
\mathbf{E} = \rho\mathbf{u}_\rho + \rho\mathbf{u}_\varphi+z\mathbf{u}_z

y en esféricas

\mathbf{E} = r\,\mathbf{u}_r + r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi
Obtenido de "http://tesla.us.es/wiki/index.php/Campos_vectoriales_en_diferentes_sistemas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:33, 3 abr 2009. - Esta página ha sido visitada 28.359 veces. - Aviso legal - Acerca de Laplace