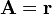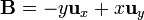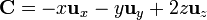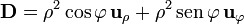Cálculo de divergencias y rotacionales
De Laplace
(→Rotacional) |
(→Campo B) |
||
| (20 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
irrotacionales y cuáles solenoidales? | irrotacionales y cuáles solenoidales? | ||
| - | + | ==Campo '''A''' == | |
| - | + | ===Divergencia=== | |
| - | + | ||
| - | + | ||
La divergencia, calculada en cartesianas, del vector de posición, es | La divergencia, calculada en cartesianas, del vector de posición, es | ||
| Línea 27: | Línea 25: | ||
<center><math>\nabla{\cdot}\mathbf{A} = \frac{1}{r^2}\frac{\partial (r^3)}{\partial r}= 3</math></center> | <center><math>\nabla{\cdot}\mathbf{A} = \frac{1}{r^2}\frac{\partial (r^3)}{\partial r}= 3</math></center> | ||
| - | + | ===Rotacional=== | |
Para el rotacional de este mismo campo, empleando coordenadas cartesianas | Para el rotacional de este mismo campo, empleando coordenadas cartesianas | ||
| Línea 49: | Línea 47: | ||
Naturalmente los resultados son los mismos independientemente del sistema empleado para calcularlos. | Naturalmente los resultados son los mismos independientemente del sistema empleado para calcularlos. | ||
| - | + | ==Campo '''B'''== | |
| - | + | ===Divergencia=== | |
Para el segundo campo, su divergencia, calculada en cartesianas, | Para el segundo campo, su divergencia, calculada en cartesianas, | ||
| Línea 72: | Línea 70: | ||
<center><math>\nabla{\cdot}\mathbf{B} = 0+0+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial \left(r\,\mathrm{sen}\,\theta\right)}{\partial \varphi} = 0</math></center> | <center><math>\nabla{\cdot}\mathbf{B} = 0+0+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial \left(r\,\mathrm{sen}\,\theta\right)}{\partial \varphi} = 0</math></center> | ||
| - | + | ===Rotacional=== | |
Para el rotacional, en cartesianas, | Para el rotacional, en cartesianas, | ||
| - | + | <center><math>\nabla\times\mathbf{B} = \left|\begin{matrix} | |
| - | \nabla\times\mathbf{B} = | + | \mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\ |
| - | + | \displaystyle\frac{\partial \ }{\partial x} & \displaystyle\frac{\partial \ }{\partial y} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ -y & x & 0\end{matrix}\right|= | |
| - | 0\mathbf{u}_{x}+0\mathbf{u}_{y}+2\mathbf{u}_{z}=2\mathbf{u}_{z} | + | 0\mathbf{u}_{x}+0\mathbf{u}_{y}+2\mathbf{u}_{z}=2\mathbf{u}_{z}</math></center> |
| - | + | ||
En cilíndricas | En cilíndricas | ||
| - | + | ||
| - | \nabla\times\mathbf{B} = \frac{1}{\rho}\ | + | <center><math>\nabla\times\mathbf{B} = \frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_{\rho} & \rho\mathbf{u}_{\varphi} & \mathbf{u}_{z} \\ & & \\ |
| - | + | \displaystyle\frac{\partial \ }{\partial \rho} &\displaystyle\frac{\partial \ }{\partial \varphi} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ 0 & \rho^2 & 0\end{matrix}\right|= | |
| - | 2\mathbf{u}_{z} | + | 2\mathbf{u}_{z}</math></center> |
| - | + | ||
y en esféricas | y en esféricas | ||
| - | + | <center><math>\nabla\times\mathbf{B} = \frac{1}{r^2\mathrm{sen}\,\theta}\left|\begin{matrix}\mathbf{u}_{r} & r\mathbf{u}_{\theta} & r\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi} \\ & & \\ | |
| - | \nabla\times\mathbf{ | + | \displaystyle \frac{\partial \ }{\partial r} &\displaystyle\frac{\partial \ }{\partial \theta} & \displaystyle\frac{\partial \ }{\partial \varphi} \\ && \\ 0 & 0 & r^2\mathrm{sen}^2\theta\end{matrix}\right|= |
| - | + | 2\cos\theta\mathbf{u}_{r}-2\,\mathrm{sen}\,\theta\mathbf{u}_{\theta}</math></center> | |
| - | 2\cos\theta\mathbf{u}_{r}-2\sen\theta\mathbf{u}_{\theta} | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | De nuevo el resultado es el mismo aunque, al estar expresado en base diferentes, parece formalmente distinto. | |
| - | == | + | ==Campo '''C'''== |
| - | ====Rotacional==== | + | ===Divergencia=== |
| + | Para el tercer campo, la divergencia en cartesianas | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{C} = -1-1+2 = 0</math></center> | ||
| + | |||
| + | En cilíndricas, aplicando los resultados del problema de [[cálculo de gradientes]] | ||
| + | |||
| + | <center><math>\mathbf{C} = -\rho\mathbf{u}_{\rho}+2z\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | y el cálculo de la divergencia da | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{C} = | ||
| + | -\frac{1}{\rho}\frac{\partial | ||
| + | \left(\rho^2\right)}{\partial \rho}+\frac{\partial (2z)}{\partial z}= -2 + 2 = 0</math></center> | ||
| + | |||
| + | y en esféricas | ||
| + | |||
| + | <center><math>\mathbf{C} = r(3\cos^2\theta-1)\mathbf{u}_{r}-3r\,\mathrm{sen}\,\theta\cos\theta\mathbf{u}_{\theta}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{C} = 3(3\cos^2\theta-1)-3(\mathrm{sen}^2\theta-2\cos^2\theta)=0</math></center> | ||
| + | |||
| + | ===Rotacional=== | ||
| + | Para el rotacional, en cartesianas | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{C} = \left|\begin{matrix} | ||
| + | \mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\ | ||
| + | \displaystyle\frac{\partial \ }{\partial x} & \displaystyle\frac{\partial \ }{\partial y} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ -x & -y & 2z\end{matrix}\right|= | ||
| + | \mathbf{0}</math></center> | ||
| + | |||
| + | En cilíndricas | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{C} = \frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_{\rho} & \rho\mathbf{u}_{\varphi} & \mathbf{u}_{z} \\ & & \\ | ||
| + | \displaystyle\frac{\partial \ }{\partial \rho} &\displaystyle\frac{\partial \ }{\partial \varphi} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ -\rho & 0 & 2z\end{matrix}\right|= | ||
| + | \mathbf{0}</math></center> | ||
| + | |||
| + | y en esféricas | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{C} = \frac{1}{r^2\mathrm{sen}\,\theta}\left|\begin{matrix}\mathbf{u}_{r} & r\mathbf{u}_{\theta} & r\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi} \\ & & \\ | ||
| + | \displaystyle \frac{\partial \ }{\partial r} &\displaystyle\frac{\partial \ }{\partial \theta} & \displaystyle\frac{\partial \ }{\partial \varphi} \\ && \\ r(3\cos^2\theta-1) & -3r^2\mathrm{sen}\,\theta\cos\theta & 0\end{matrix}\right|= | ||
| + | \mathbf{0}</math></center> | ||
| + | |||
| + | ==Campo '''D'''== | ||
| + | Por último, para el campo | ||
| + | |||
| + | <center><math>\mathbf{D} = | ||
| + | \rho^2\cos\varphi\,\mathbf{u}_{\rho}+\rho^2\mathrm{sen}\,\varphi\,\mathbf{u}_{\varphi}</math></center> | ||
| + | |||
| + | calculamos en primer lugar su divergencia y su rotacional en cilíndricas, ya que en estas coordenadas viene expresado el campo. | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{D} = 3\rho\cos\varphi +\rho\cos\varphi = 4\rho\cos\varphi</math></center> | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{D} = \frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_{\rho} & \rho\mathbf{u}_{\varphi} & \mathbf{u}_{z} \\ & & \\ | ||
| + | \displaystyle\frac{\partial \ }{\partial \rho} &\displaystyle\frac{\partial \ }{\partial \varphi} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ | ||
| + | \rho^2\cos\varphi & \rho^3\mathrm{sen}\varphi & 0\end{matrix}\right| = 4\rho\mathrm{sen}\varphi\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | Para calcular estas cantidades en cartesianas, pasamos el campo a este sistema | ||
| + | |||
| + | <center><math>\mathbf{D} = | ||
| + | \rho^2\cos\varphi(\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\varphi\mathbf{u}_{y})+\rho^2\mathrm{sen}\,\varphi\left(-\mathrm{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y}\right) | ||
| + | =\left(x^2-y^2\right)\mathbf{u}_{x}+2xy\mathbf{u}_{y}</math></center> | ||
| + | |||
| + | y calculamos su divergencia | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{D} = 2x+2x = 4x</math></center> | ||
| + | |||
| + | y su rotacional | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{D} = \left|\begin{matrix} | ||
| + | \mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\ | ||
| + | \displaystyle\frac{\partial \ }{\partial x} & \displaystyle\frac{\partial \ }{\partial y} & \displaystyle\frac{\partial \ }{\partial z} \\ && \\ x^2-y^2 & 2xy & 0\end{matrix}\right|= 4y\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | Para pasar a esféricas, primero expresamos <math>\mathbf{D}</math> en sus componentes cartesianas | ||
| + | |||
| + | <center> | ||
| + | <math>\mathbf{D}=(x^2-y^2)\mathbf{u}_{x}+2xy\mathbf{u}_{y} | ||
| + | =r^2\mathrm{sen}^2\theta\cos(2\varphi)\mathbf{u}_{x}+ r^2\mathrm{sen}^2\theta\,\mathrm{sen}(2\varphi)\mathbf{u}_{y}</math></center> | ||
| + | |||
| + | A continuación hallamos las diferentes componentes en esféricas | ||
| + | |||
| + | <center><math>D_r = \mathbf{D}{\cdot}\mathbf{u}_{r}=r^2\mathrm{sen}^3\theta\cos\varphi</math>{{qquad}}<math>D_\theta = \mathbf{D}{\cdot}\mathbf{u}_{\theta}=r^2\mathrm{sen}^2\theta\cos\theta\cos\varphi</math>{{qquad}}<math>D_\varphi = \mathbf{D}{\cdot}\mathbf{u}_{\varphi}=r^2\mathrm{sen}^2\theta\,\mathrm{sen}\varphi</math></center> | ||
| + | |||
| + | Luego, calculamos los diferentes sumandos que constituyen la divergencia | ||
| + | |||
| + | <center><math>\frac{1}{r^2}\frac{\partial \ }{\partial r}\left(r^2 D_r\right)=4r\,\mathrm{sen}^3\theta\cos\varphi</math>{{qquad}} | ||
| + | <math>\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial \ }{\partial \theta}\left(\mathrm{sen}\theta | ||
| + | D_\theta\right)=r\cos\varphi(3\,\mathrm{sen}\theta\cos^2\theta-\mathrm{sen}^3\theta)</math>{{qquad}} | ||
| + | <math>\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial \ }{\partial \varphi}(D_\varphi)=r\,\mathrm{sen}\,\theta\cos\varphi</math></center> | ||
| + | |||
| + | y, por último, sumamos | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{D}=4r\,\mathrm{sen}\,\theta\cos\varphi</math></center> | ||
| + | |||
| + | Para el rotacional | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{D} = \frac{1}{r^2\mathrm{sen}\,\theta}\left|\begin{matrix}\mathbf{u}_{r} & r\mathbf{u}_{\theta} & r\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi} \\ & & \\ | ||
| + | \displaystyle \frac{\partial \ }{\partial r} &\displaystyle\frac{\partial \ }{\partial \theta} & \displaystyle\frac{\partial \ }{\partial \varphi} \\ && \\ | ||
| + | r^2\mathrm{sen}^3\theta\cos\varphi & r^3\mathrm{sen}^2\theta\cos\theta\cos\varphi & | ||
| + | r^3\mathrm{sen}^3\theta\,\mathrm{sen}\varphi\end{matrix}\right|= | ||
| + | 4r\,\mathrm{sen}\,\theta\cos\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{r}-4r\,\mathrm{sen}^2\theta\,\mathrm{sen}\,\varphi\mathbf{u}_{\theta} | ||
| + | </math></center> | ||
| - | + | Teniendo en cuenta que | |
| - | === | + | <center><math>y=\rho\,\mathrm{sen}\,\varphi=r\,\mathrm{sen}\theta\,\mathrm{sen}\varphi</math>{{qquad}} |
| + | <math>\mathbf{u}_{z}=\cos\theta\mathbf{u}_{r}-\mathrm{sen}\,\theta\mathbf{u}_{\theta}</math></center> | ||
| - | + | puede verse que los tres resultados son coincidentes. | |
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
última version al 08:50 13 oct 2010
Contenido |
1 Enunciado
Para los campos vectoriales
calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son irrotacionales y cuáles solenoidales?
2 Campo A
2.1 Divergencia
La divergencia, calculada en cartesianas, del vector de posición, es

Para este mismo campo, en cilíndricas, sustituyendo la expresión de  dada en otro problema
dada en otro problema
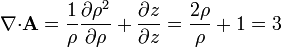
y, en esféricas,
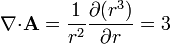
2.2 Rotacional
Para el rotacional de este mismo campo, empleando coordenadas cartesianas
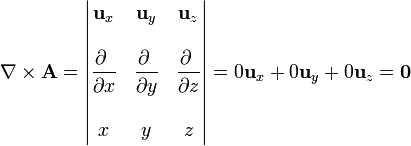
en cilíndricas
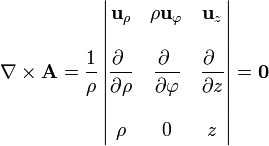
y en esféricas
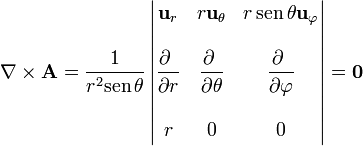
Naturalmente los resultados son los mismos independientemente del sistema empleado para calcularlos.
3 Campo B
3.1 Divergencia
Para el segundo campo, su divergencia, calculada en cartesianas,

En cilíndricas este campo se escribe
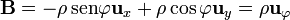
y la divergencia

En esféricas el campo es
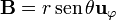
y la divergencia
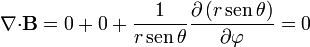
3.2 Rotacional
Para el rotacional, en cartesianas,

En cilíndricas

y en esféricas

De nuevo el resultado es el mismo aunque, al estar expresado en base diferentes, parece formalmente distinto.
4 Campo C
4.1 Divergencia
Para el tercer campo, la divergencia en cartesianas
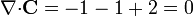
En cilíndricas, aplicando los resultados del problema de cálculo de gradientes
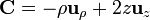
y el cálculo de la divergencia da

y en esféricas

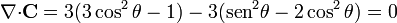
4.2 Rotacional
Para el rotacional, en cartesianas

En cilíndricas
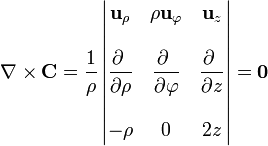
y en esféricas
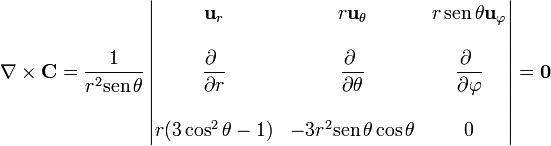
5 Campo D
Por último, para el campo
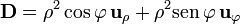
calculamos en primer lugar su divergencia y su rotacional en cilíndricas, ya que en estas coordenadas viene expresado el campo.


Para calcular estas cantidades en cartesianas, pasamos el campo a este sistema
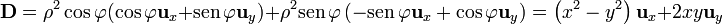
y calculamos su divergencia

y su rotacional
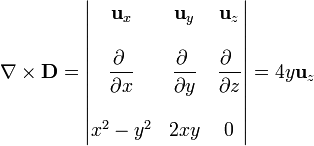
Para pasar a esféricas, primero expresamos  en sus componentes cartesianas
en sus componentes cartesianas

A continuación hallamos las diferentes componentes en esféricas


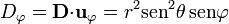
Luego, calculamos los diferentes sumandos que constituyen la divergencia



y, por último, sumamos

Para el rotacional
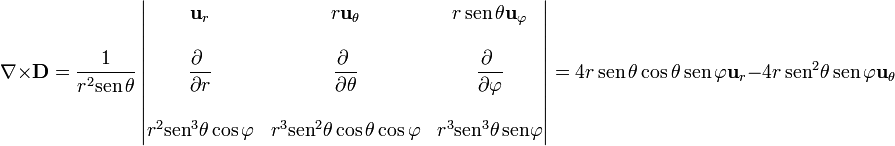
Teniendo en cuenta que

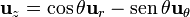
puede verse que los tres resultados son coincidentes.