Coordenadas cilíndricas. Líneas y superficies coordenadas
De Laplace
(Diferencias entre revisiones)
(→Líneas coordenadas) |
(→Enlaces) |
||
| (4 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
[[Imagen:cil-lin.png|left|frame]] | [[Imagen:cil-lin.png|left|frame]] | ||
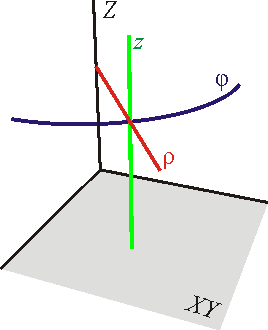
* La coordenada vertical, <math>z\,</math>, es la misma que en cartesianas, y lo mismo ocurre con su línea coordenada, que será una recta vertical que pasa por <math>P\,</math>. | * La coordenada vertical, <math>z\,</math>, es la misma que en cartesianas, y lo mismo ocurre con su línea coordenada, que será una recta vertical que pasa por <math>P\,</math>. | ||
| - | * Para la coordenada radial <math>\rho\,</math>, al mover esta coordenada nos acercamos o alejamos del eje <math>Z\,</math> sin variar la altitud ni la dirección. Las líneas serán entonces semirrectas horizontales que parten del eje <math>Z\,</math> y pasan por <math>P\,</math>. Son ''semirrectas'' y no rectas, porque <math>\rho\ | + | * Para la coordenada radial <math>\rho\,</math>, al mover esta coordenada nos acercamos o alejamos del eje <math>Z\,</math> sin variar la altitud ni la dirección. Las líneas serán entonces semirrectas horizontales que parten del eje <math>Z\,</math> y pasan por <math>P\,</math>. Son ''semirrectas'' y no rectas, porque <math>\rho\ge 0\,</math> siempre. |
* Al variar la coordenada <math> \varphi</math> cambiamos el ángulo con el eje <math>x\,</math>, sin modificar ni la distancia al eje ni la altura. Por tanto, las líneas coordenadas <math> \varphi</math> son circunferencias horizontales. | * Al variar la coordenada <math> \varphi</math> cambiamos el ángulo con el eje <math>x\,</math>, sin modificar ni la distancia al eje ni la altura. Por tanto, las líneas coordenadas <math> \varphi</math> son circunferencias horizontales. | ||
==Superficies coordenadas== | ==Superficies coordenadas== | ||
[[Imagen:cil-sup.png|right|frame]] | [[Imagen:cil-sup.png|right|frame]] | ||
| + | *Las superficies <math>z = \mathrm{cte}\,</math> son, como en cartesianas, planos horizontales. | ||
| - | = | + | *Las superficies <math>\rho = \mathrm{cte}\,</math> están formadas por los puntos situados a la misma distancia del eje <math>Z\,</math>. Estos puntos forman un cilindro circular con esta recta como eje. De aquí el nombre de este sistema de coordenadas. |
| - | + | ||
| - | + | *Si fijamos <math>\varphi</math> nos movemos sobre una superficie que forma un ángulo constante con el plano <math>XZ\,</math>. Esto viene a ser como una puerta girada un cierto ángulo respecto a su eje. La superficie coordenada es un semiplano vertical con borde el eje <math>Z\,</math>. | |
| - | + | ||
| - | == | + | ==Enlaces== |
| - | [[Coordenadas cilíndricas. Definición]] | + | * '''Siguiente:''' [[Coordenadas esféricas. Líneas y superficies coordenadas]] |
| + | * '''Anterior:''' [[Coordenadas cartesianas. Líneas y superficies coordenadas]] | ||
| + | * [[Coordenadas cilíndricas. Definición]] | ||
| + | * [[Coordenadas cilíndricas. Base vectorial]] | ||
| - | [[ | + | |
| + | [[Categoría:Líneas coordenadas|30]] | ||
| + | [[Categoría:Coordenadas cilíndricas|20]] | ||
última version al 10:21 23 nov 2007
1 Líneas coordenadas
- La coordenada vertical,
 , es la misma que en cartesianas, y lo mismo ocurre con su línea coordenada, que será una recta vertical que pasa por
, es la misma que en cartesianas, y lo mismo ocurre con su línea coordenada, que será una recta vertical que pasa por  .
.
- Para la coordenada radial
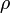 , al mover esta coordenada nos acercamos o alejamos del eje
, al mover esta coordenada nos acercamos o alejamos del eje 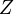 sin variar la altitud ni la dirección. Las líneas serán entonces semirrectas horizontales que parten del eje
sin variar la altitud ni la dirección. Las líneas serán entonces semirrectas horizontales que parten del eje 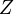 y pasan por
y pasan por  . Son semirrectas y no rectas, porque
. Son semirrectas y no rectas, porque 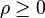 siempre.
siempre.
- Al variar la coordenada
 cambiamos el ángulo con el eje
cambiamos el ángulo con el eje  , sin modificar ni la distancia al eje ni la altura. Por tanto, las líneas coordenadas
, sin modificar ni la distancia al eje ni la altura. Por tanto, las líneas coordenadas  son circunferencias horizontales.
son circunferencias horizontales.
2 Superficies coordenadas
- Las superficies
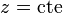 son, como en cartesianas, planos horizontales.
son, como en cartesianas, planos horizontales.
- Las superficies
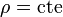 están formadas por los puntos situados a la misma distancia del eje
están formadas por los puntos situados a la misma distancia del eje  . Estos puntos forman un cilindro circular con esta recta como eje. De aquí el nombre de este sistema de coordenadas.
. Estos puntos forman un cilindro circular con esta recta como eje. De aquí el nombre de este sistema de coordenadas.
- Si fijamos
 nos movemos sobre una superficie que forma un ángulo constante con el plano
nos movemos sobre una superficie que forma un ángulo constante con el plano 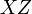 . Esto viene a ser como una puerta girada un cierto ángulo respecto a su eje. La superficie coordenada es un semiplano vertical con borde el eje
. Esto viene a ser como una puerta girada un cierto ángulo respecto a su eje. La superficie coordenada es un semiplano vertical con borde el eje 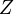 .
.