Materiales magnéticos
De Laplace
(→Magnetización) |
(→Corrientes de magnetización) |
||
| Línea 20: | Línea 20: | ||
==Corrientes de magnetización== | ==Corrientes de magnetización== | ||
| + | {{ac|Corrientes de magnetización}} | ||
| + | La expresión del potencial vector puede transformarse en suma de potenciales vectores debidos a densidades de corriente | ||
| + | |||
| + | <center><math> \mathbf{A}(\mathbf{r}) =\frac{\mu_0}{4\pi} | ||
| + | \int\frac{\mathbf{J}_m(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+\frac{\mu_0}{4\pi}\int\frac{\mathbf{K}_m(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'</math> | ||
| + | </center> | ||
| + | |||
| + | donde | ||
| + | |||
| + | <center><math>\mathbf{J}_m = \nabla\times\mathbf{M}\,</math>{{qquad}}{{qquad}}<math>\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]</math></center> | ||
| + | |||
| + | son las llamadas ''densidades de [[corriente de magnetización]]'', de volumen y de superficie, respectivamente. <math>\mathbf{K}_m</math> existe en las interfaces entre dos materiales. En el caso particular de la frontera entre un medio magnetizado y el exterior, esta densidad se reduce a <math>\mathbf{K}_m = \mathbf{M}\times\mathbf{n}</math>. | ||
| + | |||
==Ecuaciones de la magnetostática en medios materiales== | ==Ecuaciones de la magnetostática en medios materiales== | ||
Revisión de 11:05 30 mar 2009
Contenido |
1 Introducción
Este tema constituye el segundo del bloque de Magnetostática. En el se estudian brevemente las propiedades de los campos magnéticos en presencia de medios materiales, las ecuaciones que describen dichos campos y los tipos de materiales, atendiendo a sus propiedades magnéticas.
El esquema que se sigue en este tema sigue una estrecha analogía con el tema de Campo eléctrico en presencia de dieléctricos.
2 Magnetización
2.1 Definición
El campo magnético se ve afectado por la presencia de medios materiales, porque estos están constituidos por dipolos magnéticos, tanto orbitales como intrínsecos (el espín). Para describir esta distribución de dipolos en forma macroscópica se define la magnetización o imanación de un material en un punto como la densidad
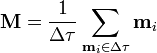
siendo Δτ un pequeño elemento de volumen en torno al punto 
.
2.2 Potencial vector de una magnetización
El potencial vector debido a una magnetización es una extensión de la expresión correspondiente a un solo dipolo
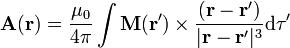
3 Corrientes de magnetización
La expresión del potencial vector puede transformarse en suma de potenciales vectores debidos a densidades de corriente
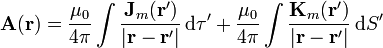
donde
![\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]](/wiki/images/math/f/7/e/f7e32e5788be56963bc508bf82ea6658.png)
son las llamadas densidades de corriente de magnetización, de volumen y de superficie, respectivamente.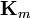 
existe en las interfaces entre dos materiales. En el caso particular de la frontera entre un medio magnetizado y el exterior, esta densidad se reduce a 
.
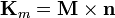