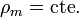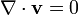Campo solenoidal
De Laplace
(→Físicos) |
(→Ejemplos) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 42: | Línea 42: | ||
<center><math>\nabla\cdot\mathbf{B} = 0</math></center> | <center><math>\nabla\cdot\mathbf{B} = 0</math></center> | ||
| - | * La densidad de corriente eléctrica en una situación de corrientes estacionarias, para las cuales la ley de conservación de la carga se reduce a | + | * La densidad de corriente eléctrica en una situación de corrientes estacionarias, para las cuales la [[ley de conservación de la carga]] se reduce a |
<center><math>\nabla\cdot\mathbf{J} +\frac{\partial \rho}{\partial t}= 0</math>{{qquad}}<math>\frac{\partial \rho}{\partial t}=0</math>{{tose}}<math>\nabla\cdot\mathbf{J} = 0</math></center> | <center><math>\nabla\cdot\mathbf{J} +\frac{\partial \rho}{\partial t}= 0</math>{{qquad}}<math>\frac{\partial \rho}{\partial t}=0</math>{{tose}}<math>\nabla\cdot\mathbf{J} = 0</math></center> | ||
| Línea 50: | Línea 50: | ||
<center><math>\nabla\cdot(\rho_m\mathbf{\mathbf{v}} +\frac{\partial \rho_m}{\partial t}= 0</math>{{qquad}}<math> \rho_m=\mathrm{cte.}\,</math>{{tose}}<math>\nabla\cdot\mathbf{v} = 0</math></center> | <center><math>\nabla\cdot(\rho_m\mathbf{\mathbf{v}} +\frac{\partial \rho_m}{\partial t}= 0</math>{{qquad}}<math> \rho_m=\mathrm{cte.}\,</math>{{tose}}<math>\nabla\cdot\mathbf{v} = 0</math></center> | ||
| + | ==Potencial vector== | ||
[[Categoría:Fundamentos matemáticos]] | [[Categoría:Fundamentos matemáticos]] | ||
última version al 15:37 23 mar 2009
Contenido |
1 Definición
Un campo cuyas fuentes escalares son nulas en todos los puntos del espacio
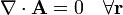
se denomina campo solenoidal.
El ejemplo más importante, en electromagnetismo, de campo solenoidal es el campo magnético \mathbf{B}, que verifica
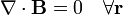
tanto en situaciones estáticas como dinámicas.
2 Líneas de campo de un campo solenoidal
Un campo solenoidal se caracteriza porque sus líneas de campo no pueden converger ni divergir de ningún punto; no pueden tener extremos localizados. Esto hace que las líneas solo puedan
- ser cerradas, o
- ir del infinito al infinito, o
- dar vueltas sobre sí mismas, sin llegar a cerrarse, como en una madeja.
3 Tubos de campo de un campo solenoidal
4 Ejemplos
4.1 Matemáticos
Un ejemplo analítico de campo solenoidal es
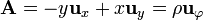
Las líneas de campo de este campo vectorial describen circunferencias en torno al eje Z, en acuerdo con la idea de que no tienen extremos.
Otro campo ligeramente diferente del anterior, pero también solenoidal, es
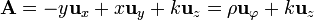
cuyas líneas de campo son hélices en torno al eje Z.
4.2 Físicos
Existen tres campos de gran importancia física que poseen la propiedad de ser solenoidales.
- El campo magnético \mathbf{B}, que satisface la ley de Gauss para el campo magnético
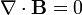
- La densidad de corriente eléctrica en una situación de corrientes estacionarias, para las cuales la ley de conservación de la carga se reduce a
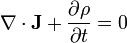
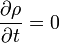

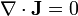
- El campo de velocidades de un líquido incompresible, que verifica la llamada ecuación de continuidad