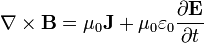Ley de Ampère

De Laplace

(Diferencias entre revisiones)

Revisión de 11:30 22 mar 2009

Contenido

1 Forma diferencial
- 1.1 Demostración
2 Límites de validez
3 Forma integral
4 Condición de salto
5 Aplicaciones
6 Ley de Ampère en medios materiales
7 La ley de Ampère-Maxwell
8 Enlaces

1 Forma diferencial

El rotacional del campo magnético puede calcularse igualmente a partir de la ley de Biot y Savart para una densidad de corriente de volumen. El resultado es la llamada Ley de Ampère (descubierta por Maxwell):

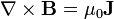
$\nabla\times\mathbf{B}=\mu_0\mathbf{J}$

La ley de Ampère expresa que el campo magnético, a diferencia del electrostático, sí posee fuentes vectoriales. Por tanto, el campo magnético no deriva de un potencial escalar.

El que las densidades de corriente sean las fuentes vectoriales del campo magnético, esto es, proporcionales a su rotacional, es coherente con la propiedad conocida de que las líneas de campo de $\mathbf{B}$ rotan en torno a las corrientes que lo crean.

1.1 Demostración

Para demostrar esta ley partiendo de la ley de Biot y Savart se aplica que

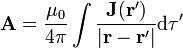
$\mathbf{B}=\nabla\times\mathbf{A}$ $\mathbf{A}=\frac{\mu_0}{4\pi}\int\frac{\mathbf{J}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'$

Aplicando que

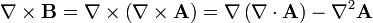
$\nabla\times\mathbf{B} = \nabla\times\left(\nabla\times\mathbf{A}\right) = \nabla\left(\nabla\cdot\mathbf{A}\right) - \nabla^2\mathbf{A}$

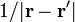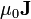resultan dos expresiones integrales. La primera se anula demostrando que este campo $\mathbf{A}$ es solenoidal (lo cual no es trivial). La segunda, tras aplicar las propiedades de $1/|\mathbf{r}-\mathbf{r}'|$ resulta ser igual a $\mu_0\mathbf{J}$ .

2 Límites de validez

A diferencia de la Ley de Gauss para el campo magnético, la ley de Ampère sólo es válida para corrientes estacionarias. Deberá ser odificada cuando existan campos o corrientes variables en el tiempo.

3 Forma integral

A partir de la forma diferencial de la Ley de Ampère puede obtenerse una expresión integral equivalente:

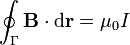
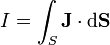
$\oint_\Gamma {{\mathbf{B}}\cdot{\mathrm{d}}{\mathbf{r}}} = {\mu_0}I$ $I = \int_S {{\mathbf{J}}\cdot{\mathrm{d}}{\mathbf{S}}}$

que, en palabras, expresa que la circulación de $\mathbf{B}$ a lo largo de una curva cerrada $Γ$ arbitraria (interpretable como la rotación neta de $\mathbf{B}$ al recorrer esta curva) es proporcional a la intensidad de corriente que atraviesa una superficie $S$ apoyada en la curva $Γ$ y orientada según la regla de la mano derecha.

La demostración es inmediata sin más que aplicar el teorema de Stokes

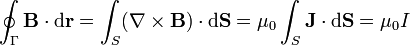
$\oint_\Gamma\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\int_S(\nabla\times\mathbf{B})\cdot\mathrm{d}\mathbf{S}=\mu_0\int_S\mathbf{J}\cdot\mathrm{d}\mathbf{S}=\mu_0I$

En la expresión integral de la ley de Ampère la elección de $S$ es arbitraria, con tal de que esté apoyada en $Γ$ . Esto es una consecuencia de que la densidad de corriente estacionaria es un campo solenoidal.

4 Condición de salto

Si tenemos una interfaz entre dos regiones, y sobre esta interfaz circula una densidad de corriente superficial 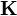$\mathbf{K}$ , las componentes tangenciales del campo magnético pueden experimentar una discontinuidad dada por la ecuación

$\mathbf{n}\times[\mathbf{B}]=\mu_0\mathbf{K}$

Para ver cómo la ley de Ampère conduce a esta condición de salto consideremos tres situaciones progresivamente más complejas

Si tenemos un hilo de corriente, las líneas de campo giran en torno al hilo.
Si tenemos un conjunto de hilos paralelos, el campo sigue envolviendo los hilos, extendiéndose tangencialmente a ellos.
Para una lámina de corriente superficial, el campo es tangencial a la superficie, pero en diferentes sentidos a cada lado, por lo que hay una discontinuidad en la componente tangencial.

Para dar un valor concreto a la ilustración anterior, supongamos que la lámina se encuentra en $x = 0$ , y la densidad de corriente va como 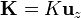$\mathbf{K} = K \mathbf{u}_z$ . La normal a esta superficie es 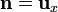$\mathbf{n} = \mathbf{u}_x$ , con lo que la condición de salto queda

${{\mathbf{u}}_x} \times \left[ {{B_x}{{\mathbf{u}}_x} + {B_y}{{\mathbf{u}}_y} + {B_z}{{\mathbf{u}}_z}} \right] = {\mu _0}K{{\mathbf{u}}_z}$

Desarrollando el producto vectorial

$-\left[ {{B_z}} \right]{{\mathbf{u}}_y} + \left[ {{B_y}} \right]{{\mathbf{u}}_z} = {\mu _0}K{{\mathbf{u}}_z}$

e igualando componente a componente

$\left[ {{B_z}} \right] = 0\,$ $\left[ {{B_y}} \right] = {\mu _0}K\,$

esto es, la componente $z$ , paralela a la corriente, es continua, mientras que la $y$ (tangente a la superficie y normal a la corriente) presenta un salto, tal como se indica en la figura.

5 Aplicaciones

Aparte de su esencial importancia teórica, la ley de Ampère es una poderosa herramienta para el cálculo de campos magnéticos en situaciones de alta simetría.

Así, permite hallar de forma sencilla

El campo magnético de un hilo infinito por el cual circula una corriente $I$

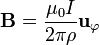
$\mathbf{B}=\frac{\mu_0I}{2\pi\rho}\mathbf{u}_\varphi$

El campo magnético de un cable cilíndrico de radio $a$ por el cual circula una densidad de corriente $J 0$

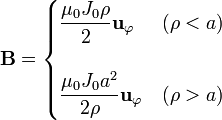
$\mathbf{B}=\begin{cases}\displaystyle\frac{\mu_0J_0\rho}{2}\mathbf{u}_\varphi & (\rho < a) \\ & \\\displaystyle\frac{\mu_0J_0a^2}{2\rho}\mathbf{u}_\varphi & (\rho > a)\end{cases}$

El campo magnético de un solenoide ideal de radio $a$ , con $n$ espiras por unidad de longitud, por las que circula una corriente $I$

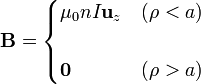
$\mathbf{B}=\begin{cases}\displaystyle \mu_0nI\mathbf{u}_z & (\rho < a) \\ & \\ \displaystyle\mathbf{0} & (\rho > a)\end{cases}$

6 Ley de Ampère en medios materiales

Artículo completo: Ley de Ampère en medios materiales

Si bien la ley de Ampère, tal como se enuncia más arriba es válida en todas las situaciones estacionarias, haya medios materiales presentes o no, en el caso de que sí los haya suele escribirse de otra forma.

En un medio material, las corrientes de desglosan en corrientes libres y corrientes de magnetización. Dado que el valor de estas últimas es normalmente desconocido a priori, se introduce el campo magnético H

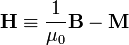
$\mathbf{H}\equiv\frac{1}{\mu_0}\mathbf{B}-\mathbf{M}$

de manera que la ley de Ampère queda como

$\nabla\times\mathbf{H}=\mathbf{J}_l$

y, en forma integral

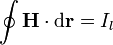
$\oint\mathbf{H}\cdot\mathrm{d}\mathbf{r}=I_l$

siendo 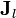$\mathbf{J}_l$ e $I l$ la densidad e intensidad de corriente libre.

7 La ley de Ampère-Maxwell

Artículo completo: Ley de Ampère-Maxwell

Como se ha indicado antes, la ley de Ampère, en la forma establecida en este artículo, sólo es válida en situaciones estacionarias.

En el caso general de sistemas variables en el tiempo, la ley de Ampère debe ser generalizada adecuadamente. Esto se consigue introduciendo la llamada corriente de desplazamiento, de forma que la le de Ampère se transforma en la ley de Ampère-Maxwell

$\nabla\times\mathbf{B}=\mu_0\mathbf{J}+\mu_0\varepsilon_0\frac{\partial\mathbf{E}}{\partial t}$

8 Enlaces

@@ Línea 104: / Línea 104: @@
 <center><math>\nabla\times\mathbf{B}=\mu_0\mathbf{J}+\mu_0\varepsilon_0\frac{\partial\mathbf{E}}{\partial t}</math></center>
+==Enlaces==
+* [[Campo magnético de corrientes estacionarias]]
+* [[Ley de Gauss para el campo magnético]]
 [[Categoría:Campo magnético de corrientes estacionarias]]

Ley de Ampère

De Laplace

Revisión de 11:30 22 mar 2009

Contenido

1 Forma diferencial

1.1 Demostración

2 Límites de validez

3 Forma integral

4 Condición de salto

5 Aplicaciones

6 Ley de Ampère en medios materiales

7 La ley de Ampère-Maxwell

8 Enlaces

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES