Problemas de campo magnético (GIE)
De Laplace
(→Campo magnético producido por una bobina cilíndrica) |
(→Efecto de una espira sobre una carga) |
||
| (14 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | =Problemas de boletín= | ||
==[[Movimiento de una carga en un campo magnético]]== | ==[[Movimiento de una carga en un campo magnético]]== | ||
Una carga puntual de masa <math>m</math> y carga <math>q</math> se encuentra inmersa en un campo magnético uniforme <math>\vec{B}=B_0\vec{k}</math>. La carga se encuentra inicialmente en el origen de coordenadas. | Una carga puntual de masa <math>m</math> y carga <math>q</math> se encuentra inmersa en un campo magnético uniforme <math>\vec{B}=B_0\vec{k}</math>. La carga se encuentra inicialmente en el origen de coordenadas. | ||
| Línea 11: | Línea 12: | ||
==[[Fuerza magnética sobre una espira cuadrada]]== | ==[[Fuerza magnética sobre una espira cuadrada]]== | ||
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme <math>\vec{B}=B_0\vec{k}</math> en el semiespacio | El campo entre los polos de un imán se puede modelar como un campo magnético uniforme <math>\vec{B}=B_0\vec{k}</math> en el semiespacio | ||
| - | <math>x>b</math>. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que sus vértices se hallan en <math>\pm a\vec{\imath}</math> y en <math>\pm a\vec{\jmath}</math>. Por la espira circula una intensidad de corriente <math>I</math>. Calcule la fuerza sobre cada lado de la espira como función y la fuerza neta (distínganse los casos necesarios). | + | <math>x>b</math>. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que sus vértices se hallan en <math>\pm a\vec{\imath}</math> y en <math>\pm a\vec{\jmath}</math>. Por la espira circula una intensidad de corriente <math>I</math>. Calcule la fuerza sobre cada lado de la espira como función de lo que penetra la espira en el campo y la fuerza neta (distínganse los casos necesarios). |
| + | |||
| + | <center>[[Archivo:espira-parcial-campo-01.png]]</center> | ||
==[[Fuerza magnética sobre una espira inclinada]]== | ==[[Fuerza magnética sobre una espira inclinada]]== | ||
| Línea 37: | Línea 40: | ||
Dos cargas puntuales iguales +1.0 nC se mueven con la misma rapidez <math>v_0=100\,\mathrm{km}/\mathrm{s}</math> de forma que en un instante se encuentran situadas en <math>\vec{r}_1=\vec{0}</math> y <math>\vec{r}_2 = 2\vec{\imath}\,\mathrm{m}</math>, respectivamente. | Dos cargas puntuales iguales +1.0 nC se mueven con la misma rapidez <math>v_0=100\,\mathrm{km}/\mathrm{s}</math> de forma que en un instante se encuentran situadas en <math>\vec{r}_1=\vec{0}</math> y <math>\vec{r}_2 = 2\vec{\imath}\,\mathrm{m}</math>, respectivamente. | ||
| - | Calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra. ¿Cuál es la proporción entre estas dos fuerzas? | + | Calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra si se mueven paralelamente en la dirección del eje Z. ¿Cuál es la proporción entre estas dos fuerzas? |
¿Cómo cambian estas fuerzas si se cambia el signo de una de las cargas, el sentido de una de las velocidades, o ambas cosas a la vez? | ¿Cómo cambian estas fuerzas si se cambia el signo de una de las cargas, el sentido de una de las velocidades, o ambas cosas a la vez? | ||
| Línea 44: | Línea 47: | ||
Newton? | Newton? | ||
| - | ==[[Campo magnético producido por una espira circular]]== | + | ==[[Campo_magnético_creado_por_corrientes_(GIE)#Campo_de_una_espira_circular|Campo magnético producido por una espira circular]]== |
Halle el campo magnético en los puntos del eje de una espira circular de radio <math>a</math>, por la cual circula una corriente <math>I_0</math>. | Halle el campo magnético en los puntos del eje de una espira circular de radio <math>a</math>, por la cual circula una corriente <math>I_0</math>. | ||
| - | ==[[Campo magnético producido por una bobina cilíndrica]]== | + | ==[[Campo_magnético_creado_por_corrientes_(GIE)#Campo_de_un_solenoide_finito|Campo magnético producido por una bobina cilíndrica]]== |
A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud <math>h</math> y radio <math>a</math> con <math>N</math> espiras. ¿A qué tiende el resultado cuando <math>h\gg a</math>? | A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud <math>h</math> y radio <math>a</math> con <math>N</math> espiras. ¿A qué tiende el resultado cuando <math>h\gg a</math>? | ||
| + | |||
| + | ==[[Campo magnético producido por una espira rectangular]]== | ||
| + | Halle el campo magnético producido por un segmento rectilíneo de corriente de longitud <math>h</math>, por el cual circula una corriente <math>I_0</math> en cualquier punto del espacio. Para fijar ideas, sitúese el eje OZ sobre el segmento, extendiéndose éste desde <math>\overrightarrow{OA}=a\vec{k}</math> a <math>\overrightarrow{OB}=b\vec{k}</math> (<math>b>a</math>) con la corriente de A a B, y hállese el campo en un punto <math>\overrightarrow{OP}=x\vec{\imath}</math>. Posteriormente generalícese el resultado. | ||
| + | |||
| + | A partir del resultado anterior, hállese el campo magnético en el centro de una espira rectangular de lados <math>a</math> y <math>b</math> por la cual circula una corriente <math>I_0</math>. | ||
==[[Fuerza magnética entre dos hilos paralelos]]== | ==[[Fuerza magnética entre dos hilos paralelos]]== | ||
| Línea 61: | Línea 69: | ||
Para el caso particular <math>a=2\,\mathrm{cm}</math> <math>I_0=0.1\,\mathrm{A}</math>, ¿cuánto vale el campo magnético en el origen | Para el caso particular <math>a=2\,\mathrm{cm}</math> <math>I_0=0.1\,\mathrm{A}</math>, ¿cuánto vale el campo magnético en el origen | ||
de coordenadas para los dos casos anteriores? | de coordenadas para los dos casos anteriores? | ||
| - | + | <!-- | |
==[[Campo magnético producido por un cable grueso]]== | ==[[Campo magnético producido por un cable grueso]]== | ||
Calcule el campo magnético debido a un cable cilíndrico grueso, de radio <math>a</math> y gran longitud, por el cual circula una corriente | Calcule el campo magnético debido a un cable cilíndrico grueso, de radio <math>a</math> y gran longitud, por el cual circula una corriente | ||
<math>I_0</math> distribuida uniformemente en su sección. Si <math>I_0=100\,\mathrm{mA}</math> y <math>a=1\,\mathrm{mm}</math>, ¿cuánto vale el máximo campo magnético que produce el hilo? | <math>I_0</math> distribuida uniformemente en su sección. Si <math>I_0=100\,\mathrm{mA}</math> y <math>a=1\,\mathrm{mm}</math>, ¿cuánto vale el máximo campo magnético que produce el hilo? | ||
| + | --> | ||
| + | =Problemas adicionales= | ||
| + | ==[[Corriente y campo magnético de dos hilos]]== | ||
| + | Se tienen dos hilos de cobre de gran longitud <math>b=20.0\,\mathrm{m}</math>. Uno de ellos tiene un diámetro <math>D_1=1\,\mathrm{mm}</math> y el otro <math>D_2=2\,\mathrm{mm}</math>. Se sitúan paralelamente a una distancia <math>d= 10\,\mathrm{cm}</math> y se conectan sus extremos de forma que constituyen una asociación en paralelo. Entre los extremos de la asociación se aplica una diferencia de potencial <math>V_0= 1.0\,\mathrm{V}</math>. | ||
| + | |||
| + | # Calcule la intensidad de corriente que circula por cada uno de los hilos. | ||
| + | # ¿Cuál es la potencia total disipada en el sistema? | ||
| + | # Halle el vector campo magnético producido por los hilos en el punto O, centro del sistema. | ||
| + | # Empleando los ejes de la figura, ¿en qué punto del eje OX se anula el campo magnético? | ||
| + | |||
| + | <center>[[Archivo:dos-hilos-distintos.png]]</center> | ||
| + | |||
| + | '''Dato:''' Conductividad del cobre, <math>\sigma = 5.96\times 10^7\mathrm{S}/\mathrm{m}</math>; permeabilidad del vacío <math>\mu_0=4\pi\times 10^{-7}\mathrm{T}\cdot\mathrm{m}/\mathrm{A}</math>; campo magnético creado por un hilo infinito, expresado en cilíndricas, | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0I}{2\pi\rho}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | =[[Preguntas de test de campo magnético (GIE)|Preguntas de test]]= | ||
| + | ==Espiras paralelas== | ||
| + | Dos espiras circulares se sitúan de la manera indicada en la figura, con las intensidades de corriente en los sentidos que se indican. ¿Cómo es la interacción de la inferior sobre la superior? | ||
| + | |||
| + | <center>[[Archivo:dos-espiras-paralelas.png]]</center> | ||
| + | |||
| + | :*'''A''' La atrae. | ||
| + | :*'''B''' No ejerce ninguna interacción | ||
| + | :*'''C''' La repele. | ||
| + | :*'''D''' Aparece un par de fuerzas que tiende a darle la vuelta. | ||
| + | |||
| + | ==Fuerza entre cargas en movimiento== | ||
| + | Dos cargas eléctricas iguales se mueven por el eje Z. En un instante dado una se encuentra en el origen moviéndose con <math>+v_0\vec{k}</math> y la otra en <math>a\vec{k}</math> moviéndose con <math>-v_0\vec{k}</math>. ¿Cómo es la fuerza magnética entre las cargas? | ||
| + | |||
| + | :*'''A''' Atractiva. | ||
| + | :*'''B''' Repulsiva. | ||
| + | :*'''C''' Nula. | ||
| + | :*'''D''' Perpendicular al eje Z. | ||
| + | |||
| + | ==Efecto de una espira sobre una carga== | ||
| + | Se tiene una espira circular en el plano XY, centrada en el origen, por la cual circula una corriente <math>I_0</math> en sentido antihorario. Por el centro de la espira pasa una carga positiva <math>+q</math>, moviéndose con velocidad <math>\vec{v}=v_0\vec{\imath}</math>. ¿Qué efecto produce la espira sobre la carga? | ||
| + | |||
| + | :*'''A''' Una fuerza en el sentido <math>-\vec{\jmath}</math>. | ||
| + | :*'''B''' Una fuerza en el sentido <math>\vec{k}</math>. | ||
| + | :*'''C''' Una fuerza en el sentido <math>\vec{\imath}</math>. | ||
| + | :*'''D''' Ninguno, ya que el campo es nulo en el centro de la espira | ||
| + | |||
| + | ==Comparación de bobinas== | ||
| + | ¿Cuál de las siguientes bobinas produce un campo magnético más intenso en su interior cuando por ellas circula una corriente de 1 A? | ||
| + | |||
| + | :*'''A''' Una de 300 vueltas, 15 cm de longitud y 2 cm de diámetro. | ||
| + | :*'''B''' Una de 200 vueltas, 8 cm de longitud y 1 cm de diámetro. | ||
| + | :*'''C''' Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro. | ||
| + | :*'''D''' Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro. | ||
| + | |||
| + | ==Variación del radio de una espira== | ||
| + | Se aumenta el radio de una espira circular por 4. ¿Por cuánto hay que multiplicar la corriente que circula por ella para que produzca el mismo campo magnético en su centro? | ||
| + | |||
| + | :*'''A''' Es indiferente, porque el campo justo en el centro es nulo. | ||
| + | :*'''B''' Por 4. | ||
| + | :*'''C''' Por 2. | ||
| + | :*'''D''' Por 16. | ||
| + | [[Categoría:Campo magnético (GIE)]] | ||
| + | [[Categoría: Problemas de campo magnético (GIE)]] | ||
última version al 15:56 19 abr 2020
1 Problemas de boletín
1.1 Movimiento de una carga en un campo magnético
Una carga puntual de masa m y carga q se encuentra inmersa en un campo magnético uniforme 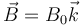 . La carga se encuentra inicialmente en el origen de coordenadas.
. La carga se encuentra inicialmente en el origen de coordenadas.
- Suponga que la velocidad inicial de la partícula es nula. ¿Cuánto vale la fuerza magnética sobre ella y cómo es el movimiento posterior?
- ¿Y si la velocidad inicial es
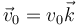 ?
?
- Suponga ahora que velocidad inicial es
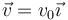
- ¿Cuánto vale la fuerza sobre la carga en el instante inicial? ¿Y su aceleración? ¿Y las componentes intrínsecas de esta?
- ¿Cuánto vale la rapidez de la partícula en todo instante?
- Como consecuencia de la acción de la fuerza magnética, la carga describe un movimiento circular. ¿Cuánto vale el radio de la circunferencia?
1.2 Fuerza magnética sobre una espira cuadrada
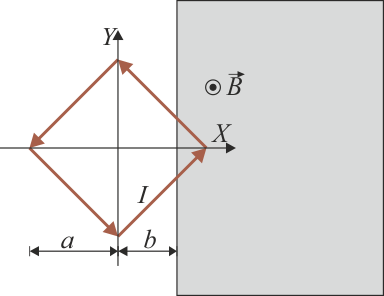
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme 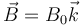 en el semiespacio
x > b. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que sus vértices se hallan en
en el semiespacio
x > b. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que sus vértices se hallan en 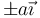 y en
y en 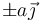 . Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira como función de lo que penetra la espira en el campo y la fuerza neta (distínganse los casos necesarios).
. Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira como función de lo que penetra la espira en el campo y la fuerza neta (distínganse los casos necesarios).
1.3 Fuerza magnética sobre una espira inclinada
Una espira cuadrada ABCD de lado 10 cm se encuentra en el interior de un campo magnético uniforme 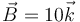 (mT). Los vértices de la espira se encuentran en
(mT). Los vértices de la espira se encuentran en
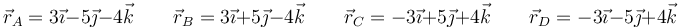
(distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD.
- Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira
- Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley
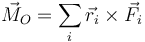
- Calcule el momento magnético de la espira y compruebe que

1.4 Fuerza magnética entre dos cargas puntuales
Dos cargas puntuales iguales +1.0 nC se mueven con la misma rapidez 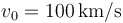 de forma que en un instante se encuentran situadas en
de forma que en un instante se encuentran situadas en 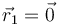 y
y 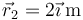 , respectivamente.
, respectivamente.
Calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra si se mueven paralelamente en la dirección del eje Z. ¿Cuál es la proporción entre estas dos fuerzas?
¿Cómo cambian estas fuerzas si se cambia el signo de una de las cargas, el sentido de una de las velocidades, o ambas cosas a la vez?
Calcule el valor de estas fuerzas si 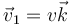 ,
, 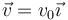 . ¿Se verifica la tercera ley de
Newton?
. ¿Se verifica la tercera ley de
Newton?
1.5 Campo magnético producido por una espira circular
Halle el campo magnético en los puntos del eje de una espira circular de radio a, por la cual circula una corriente I0.
1.6 Campo magnético producido por una bobina cilíndrica
A partir del caso anterior, calcule el campo magnético debido a una bobina de longitud h y radio a con N espiras. ¿A qué tiende el resultado cuando 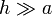 ?
?
1.7 Campo magnético producido por una espira rectangular
Halle el campo magnético producido por un segmento rectilíneo de corriente de longitud h, por el cual circula una corriente I0 en cualquier punto del espacio. Para fijar ideas, sitúese el eje OZ sobre el segmento, extendiéndose éste desde 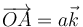 a
a 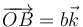 (b > a) con la corriente de A a B, y hállese el campo en un punto
(b > a) con la corriente de A a B, y hállese el campo en un punto 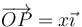 . Posteriormente generalícese el resultado.
. Posteriormente generalícese el resultado.
A partir del resultado anterior, hállese el campo magnético en el centro de una espira rectangular de lados a y b por la cual circula una corriente I0.
1.8 Fuerza magnética entre dos hilos paralelos
Se tienen dos hilos paralelos, de longitud indefinida, separados una distancia a. Calcule la fuerza magnética sobre una porción de longitud h de uno de los hilos debida al otro cuando por ellos circulan corrientes I1 e I2.
1.9 Campo magnético producido por dos hilos paralelos
Dos hilos paralelos se hallan situados paralelamente al eje Z, situados sobre 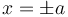 , y = 0. Determine el valor del campo magnético en todos los puntos del plano x = 0, y en todos los puntos del plano y = 0 en los dos casos siguientes:
, y = 0. Determine el valor del campo magnético en todos los puntos del plano x = 0, y en todos los puntos del plano y = 0 en los dos casos siguientes:
- Por los hilos circulan corrientes paralelas + I0.
- Por los hilos circulan corrientes antiparalelas
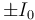 .
.
Para el caso particular 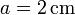
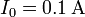 , ¿cuánto vale el campo magnético en el origen
de coordenadas para los dos casos anteriores?
, ¿cuánto vale el campo magnético en el origen
de coordenadas para los dos casos anteriores?
2 Problemas adicionales
2.1 Corriente y campo magnético de dos hilos
Se tienen dos hilos de cobre de gran longitud 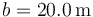 . Uno de ellos tiene un diámetro
. Uno de ellos tiene un diámetro 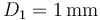 y el otro
y el otro 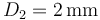 . Se sitúan paralelamente a una distancia
. Se sitúan paralelamente a una distancia 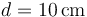 y se conectan sus extremos de forma que constituyen una asociación en paralelo. Entre los extremos de la asociación se aplica una diferencia de potencial
y se conectan sus extremos de forma que constituyen una asociación en paralelo. Entre los extremos de la asociación se aplica una diferencia de potencial 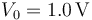 .
.
- Calcule la intensidad de corriente que circula por cada uno de los hilos.
- ¿Cuál es la potencia total disipada en el sistema?
- Halle el vector campo magnético producido por los hilos en el punto O, centro del sistema.
- Empleando los ejes de la figura, ¿en qué punto del eje OX se anula el campo magnético?
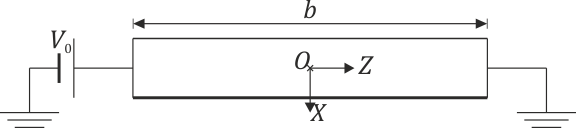
Dato: Conductividad del cobre, 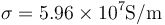 ; permeabilidad del vacío
; permeabilidad del vacío 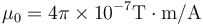 ; campo magnético creado por un hilo infinito, expresado en cilíndricas,
; campo magnético creado por un hilo infinito, expresado en cilíndricas,
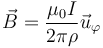
3 Preguntas de test
3.1 Espiras paralelas
Dos espiras circulares se sitúan de la manera indicada en la figura, con las intensidades de corriente en los sentidos que se indican. ¿Cómo es la interacción de la inferior sobre la superior?
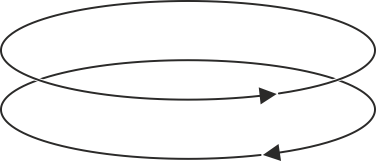
- A La atrae.
- B No ejerce ninguna interacción
- C La repele.
- D Aparece un par de fuerzas que tiende a darle la vuelta.
3.2 Fuerza entre cargas en movimiento
Dos cargas eléctricas iguales se mueven por el eje Z. En un instante dado una se encuentra en el origen moviéndose con 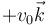 y la otra en
y la otra en 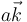 moviéndose con
moviéndose con 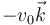 . ¿Cómo es la fuerza magnética entre las cargas?
. ¿Cómo es la fuerza magnética entre las cargas?
- A Atractiva.
- B Repulsiva.
- C Nula.
- D Perpendicular al eje Z.
3.3 Efecto de una espira sobre una carga
Se tiene una espira circular en el plano XY, centrada en el origen, por la cual circula una corriente I0 en sentido antihorario. Por el centro de la espira pasa una carga positiva + q, moviéndose con velocidad 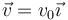 . ¿Qué efecto produce la espira sobre la carga?
. ¿Qué efecto produce la espira sobre la carga?
- A Una fuerza en el sentido
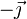 .
.
- B Una fuerza en el sentido
 .
.
- C Una fuerza en el sentido
 .
.
- D Ninguno, ya que el campo es nulo en el centro de la espira
- A Una fuerza en el sentido
3.4 Comparación de bobinas
¿Cuál de las siguientes bobinas produce un campo magnético más intenso en su interior cuando por ellas circula una corriente de 1 A?
- A Una de 300 vueltas, 15 cm de longitud y 2 cm de diámetro.
- B Una de 200 vueltas, 8 cm de longitud y 1 cm de diámetro.
- C Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro.
- D Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro.
3.5 Variación del radio de una espira
Se aumenta el radio de una espira circular por 4. ¿Por cuánto hay que multiplicar la corriente que circula por ella para que produzca el mismo campo magnético en su centro?
- A Es indiferente, porque el campo justo en el centro es nulo.
- B Por 4.
- C Por 2.
- D Por 16.





